考虑科里奥利力以后抛体的运动情况

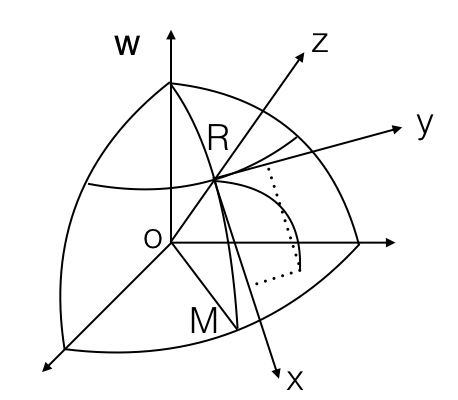
如下图所示，选取与抛体出射点固连的动系

$$R-xyz$$
我们真正关心的问题是，已知炮弹的出射点的经度和纬度，出射炮弹的方位角 $$\alpha ,\beta, \gamma$$ 如何计算炮弹落点的经度和纬度

描述炮弹在动系中运动的微分方程:

$$设<\vec{OR},\vec{OM}>=\varphi$$
在动系中角速度的表达式：
$$\vec{\omega}=-\omega cos\varphi \vec{i}+\omega sin\varphi \vec{k}$$
炮弹在动系中相对速度的表达式：
$$\vec{V^{'}}={\frac{\mathrm{d} x}{\mathrm{d} t}} \vec{i}+{\frac{\mathrm{d} y}{\mathrm{d} t}} \vec{j}+{\frac{\mathrm{d} z}{\mathrm{d} t}} \vec{k}$$
则科里奥利力的表达式为
$$\vec{F_{co}}=-2m \vec{\omega}\times\vec{V^{'}}$$
另一方面空气阻力的表达式为：
$$\vec{F_{drag}}=-Be^{-\frac{h}{h_0}}(VV_x\vec{i}+VV_y\vec{j}+VV_z\vec{k})$$
惯性离心力和地球万有引力的合力可由重力代替：
$$G=-mg\vec{k}$$
综上可以给出炮弹在动系中的运动微分方程：
$$m\ddot{x}=2mw\dot{y}sin\varphi-Be^{-\frac{h}{h_0}}(VV_x)$$
$$m\ddot{y}=-2m(\dot{z}cos\varphi+\dot{x}sin\varphi)-Be^{-\frac{h}{h_0}}(VV_y)$$
$$m\ddot{z}=2mw\dot{y}cos\varphi-Be^{-\frac{h}{h_0}}(VV_z)-mg$$
$$其中h_0=1\times10^4m,h为炮弹距离地表的距离, h=\sqrt{x^2+y^2+(z+R)^2}-R$$
$$R为地球半径，R＝6.371\times10^6m$$

微分方程的数值计算处理:

• 微分方程的离散化
  $$x_{i+1}=x_{i}+V_{x,i}\Delta{t}$$
  $$V_{x,i+1}=V_{x,i}+2wV_{y,i}sin\varphi\Delta{t}-\frac{Be^{-\frac{h}{h_0}}(V_{i}V_{x,i})}{m}\Delta{t}$$
  $$y_{i+1}=y_{i}+V_{y,i}\Delta{t}$$
  $$V_{y,i+1}=V_{y,i}-2(V_{z,i}cos\varphi+V_{x,i}sin\varphi)\Delta{t}-\frac{Be^{-\frac{h}{h_0}}(V_{i}V_{y,i})}{m}\Delta{t}$$
  $$z_{i+1}=z_{i}+V_{z,i}\Delta{t}$$
  $$V_{z,i+1}=V_{z,i}+2wV_{y,i}cos\varphi\Delta{t}-\frac{Be^{-\frac{h}{h_0}}(V_{i}V_{z,i})}{m}\Delta{t}-g\Delta{t}$$
  $$常数的取值g=9.8m/s^{2},\frac{B}{m}=4\times10^{-5}m^{-1},\omega=7.3\times10^{-5}s^{-1},R＝6.371\times10^6m$$
  
  • 初始条件及落地条件的处理
    怎样判定炮弹落地，并且根据落点位置给出炮弹的经纬度是计算的核心问题。
    假定初始时炮弹的经纬度为：
    $$(\theta_0,\varphi_0)$$
    
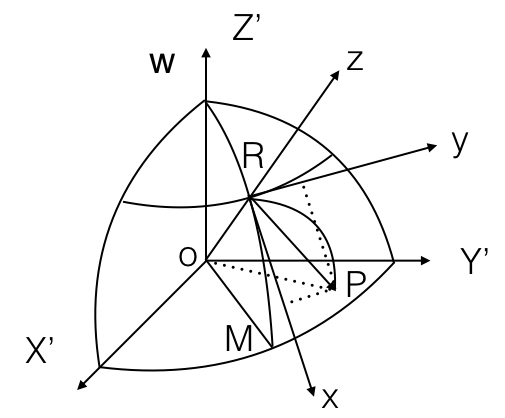
    即：
    $$<\vec{OR},\vec{OZ{'}}>=\varphi_0,<\vec{OM},\vec{OX{'}}>=\theta_0$$
    判断炮弹是否落地，可以通过判断
    $$h=\sqrt{x^2+y^2+(z+R)^2}-R=^{?}0$$
    得到炮弹落地的坐标（x,y,z）以后计算落点的经纬度
    $$(\theta,\varphi)$$
    $$\vec{RP}=(x,y,z),其在平面OMR上的投影为 \vec{RP_{OMR}}=(x,0,z),其和 \vec{OR} 的夹角即为纬度的增量$$
    $$\vec{RP}在平面OX^{'}Y^{'}上的投影，可以通过\vec{RP}减去其在平面法向量上的投影得出$$
    $$\vec{RP_{OX^{'}Y^{'}}}=\vec{RP}-\vec{RP}* \frac{\vec{OZ^{'}}}{|\vec{OZ^{'}}|}\vec{n_{oz^{'}}}$$
    $$计算\vec{RP_{OX^{'}Y^{'}}}与\vec{OM}的夹角即可得出经度的增量$$
    $$\vec{RP_{OX^{'}Y^{'}}}=(x,y,z)-(x,y,z)*(-cos\varphi,0,sin\varphi)(-cos\varphi,0,sin\varphi)$$
    $$\vec{OM}=Rcos(\varphi)\vec{i}+Rsin(\varphi)\vec{k}$$
  • 至此数值计算的理论基础已经完成

计算实例:

注：经度全是东经，纬度全是南纬
随便选一点发射

（方位角）与X轴夹角	与Y轴夹角	与Z轴夹角	初速度 初始经度	初始纬度	初速度 m/s		落点经度	落点纬度
45	45	0	20	20	700		74.44	160

轨迹图：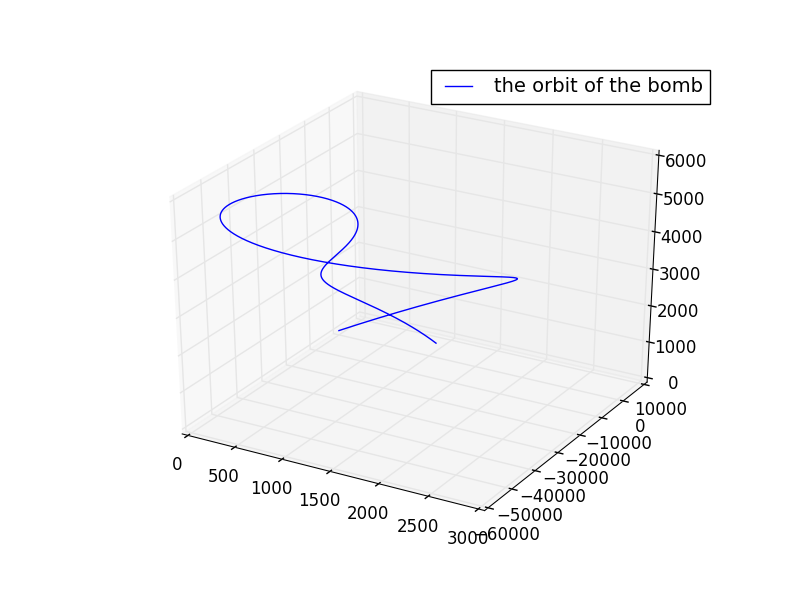

选极点向上发射

（方位角）与X轴夹角	与Y轴夹角	与Z轴夹角	初速度 初始经度	初始纬度	初速度 m/s		落点经度	落点纬度
90	90	0	0	90	700		0.00	90.0

轨迹图：

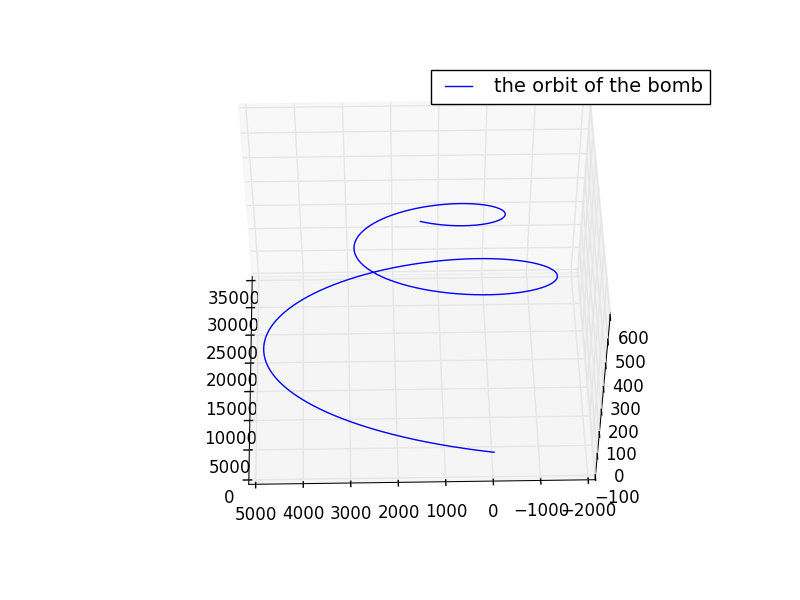
在武汉大学发射

（方位角）与X轴夹角	与Y轴夹角	与Z轴夹角	初速度 初始经度	初始纬度	初速度 m/s		落点经度	落点纬度
90	90	0	60	114	700		-24	133

轨迹图：

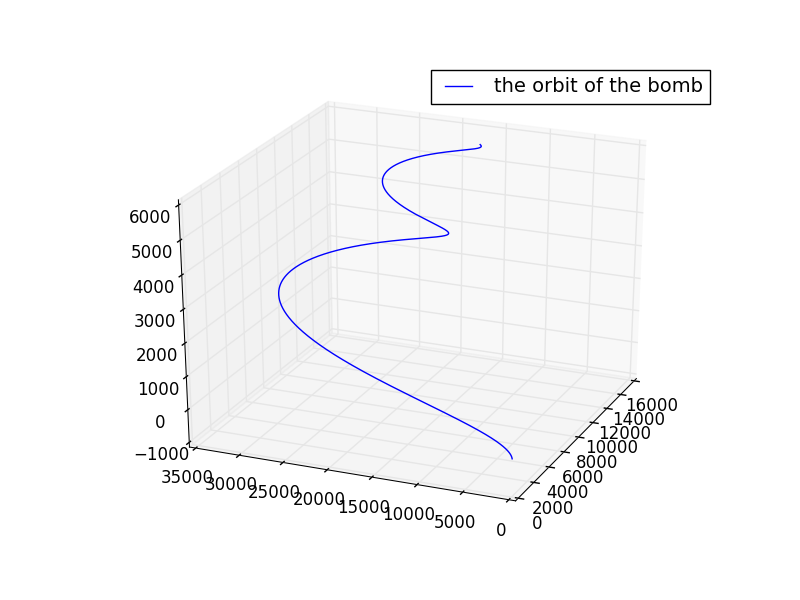
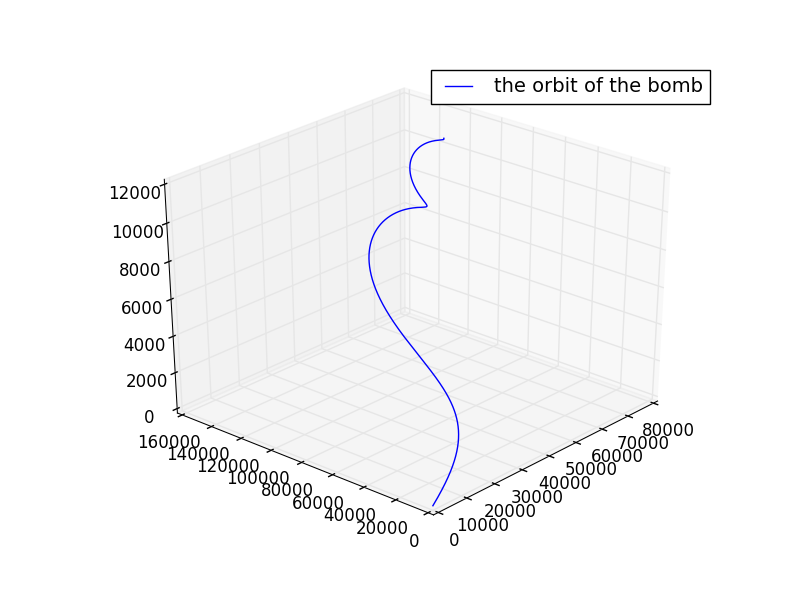
以略大于第一宇宙速度的速度发射
轨迹图：

计算程序（估计计算会有错误）

#coding:utf-8
#initial value
import math 
t=[]
dt=0.01    #B/m=4*10-5 realy count
g=9.8
end_time=100
h_0=0.0001
B=4*10**(-5)
a=45/180.0*math.pi
b=45/180.0*math.pi
c=0/180.0*math.pi
theta=[a,b,c]   #direction angle
d=20/180.0*math.pi
e=math.pi/2-20/180.0*math.pi
angle_0=[d,e]  #initial longitude and latitude
t.append(0)
w=4.167*10**-3
R=6371000
#define variable 
x=[]
v_x=[]
y=[]
v_y=[]
z=[]
v_z=[]
x.append(0)
y.append(0)
z.append(0)
v_x.append(700*math.cos(theta[0]))  #initial speed equal 700m/s
v_y.append(700*math.cos(theta[1]))
v_z.append(700*math.cos(theta[2]))
#caulate the coordinate
for i in range(int(end_time/dt)):
    m=x[i]+v_x[i]*dt
    x.append(m)
    n=v_x[i]+2*w*v_y[i]*math.sin(angle_0[1])*dt-B*math.e**-(((x[i]**2+y[i]**2+(z[i]+R)**2)**0.5-R)*h_0)*((v_x[i]**2+v_y[i]**2+v_z[i]**2)**0.5)*v_x[i]*dt
    v_x.append(n)
    o=y[i]+v_y[i]*dt
    y.append(o)
    p=v_y[i]-2*(v_z[i]*math.cos(angle_0[1])+v_x[i]*math.sin(angle_0[1]))*dt-B*math.e**-(((x[i]**2+y[i]**2+(z[i]+R)**2)**0.5-R)*h_0)*((v_x[i]**2+v_y[i]**2+v_z[i]**2)**0.5)*v_y[i]*dt
    v_y.append(p)
    r=z[i]+v_z[i]*dt
    z.append(r)
    s=v_z[i]+2*w*v_y[i]*math.cos(angle_0[1])*dt-g*dt-B*math.e**-(((x[i]**2+y[i]**2+(z[i]+R)**2)**0.5-R)*h_0)*((v_x[i]**2+v_y[i]**2+v_z[i]**2)**0.5)*v_z[i]*dt
    v_z.append(s)
    H=(x[i]**2+y[i]**2+(z[i]+R)**2)**0.5-R
    if H<=0:
       if H>=-3:
          X=x[-1]
          Y=y[-1]
          Z=z[-1]
          print x[-1],y[-1],z[-1]
#caulate the longitude and latitude  
          Delta_g=math.pi/2-math.acos(Z/((X**2+Y**2)**0.5))
          g=Delta_g+angle_0[1]
         # k_1=X*math.cos(angle_0[1])-(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1]))*math.cos(angle_0[1])**2+Z*math.sin(angle_0[1])+(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1])*math.sin(angle_0[1])**2
         # k_2=(X-(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1])*math.cos(angle_0[1])))**2+Y**2+(Z+(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1]))*math.sin(angle_0[1]))**2
         # k=k_1
          k_1=X*math.cos(angle_0[1])-(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1]))*math.cos(angle_0[1])**2+Z*math.sin(angle_0[1])+(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1]))*math.sin(angle_0[1])**2
          k_2=(X-(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1])*math.cos(angle_0[1])))**2+Y**2+(Z+(X*math.cos(angle_0[1])-Z*math.sin(angle_0[1]))*math.sin(angle_0[1]))**2
          Delta_f=k_1/k_2**0.5
          f=Delta_f+angle_0[0]
          f_1=(f/math.pi)*180
          g_1=(g/math.pi)*180
          print f_1 ,"longitude"
          print g_1 ,"latitude"
         # print k,"X"
#draw the picture
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure()
ax = fig.gca(projection='3d'）
ax.plot(x, y, z, label='parametric curve')
ax.legend()
plt.show()

参考文献

• 经典力学（上） 王波 武汉大学出版社

• 计算物理教材