homework_6

摘要：

本文主要分析抛体在空气阻力作用下的运动情况 ，以炮弹为实际情景来讨论不同情况下炮弹的射程。本文主要分析的影响因素：
1.空气阻力
2.高度对空气阻力的影响
3.炮弹的出射角度
本文的局限性在于没有考虑运动过程中科里奥利里力的影响，近似认为炮弹在一个平面内运动。(考虑科里奥利力的情形将在下一篇给出）

正文：

在不考虑空气阻力的情况下抛体的运动很容易给出解析解。为了验证数值计算的精度，可以将数值解与解析解做比较。抛体的运动参数取取值如下：

$$g=9.8m/s^2$$ $$v_0=700m/s$$
此时抛体的射程为：
$$x= \frac{v_0^2sin2\theta}{g}$$
通过数值计算给出的结果如下面的图标所示：

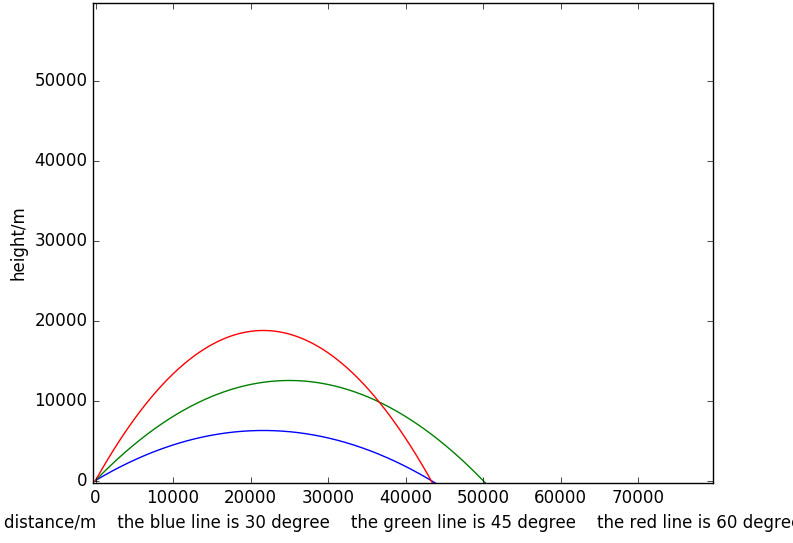
此时三种角度出射炮弹的射程为：

30度	45度	60度
43387.1m	49838.7m	43387.1m

以45度为例解析解的射程为50000m, 此时相对误差为0.32%.
而且数值解至少有两个特征符合物理事实：
1.角度为45度时射程最远。
2.角度和为90度的两种炮弹射程相同。

考虑空气阻力的影响但是忽略空气阻力随高度的变化。抛体的动力学方程为

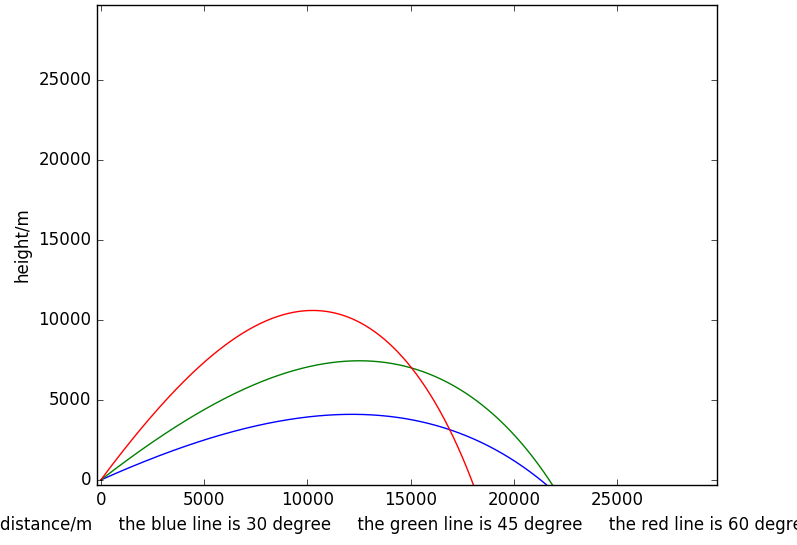
图中抛体运动的参数取值：

$$g=9.8m/s^2$$ $$\frac{B_2}{m}=4*10^-5$$ $$v_0=700m/s$$
通过在图上取点可以得出三个炮弹的射程
三个炮弹的射程见下表

\	30 度	45度	60 度
射程	21229.8m	21774.2m	17903.2m

在考虑空气阻力随炮弹高度变化的情况下炮弹的射程分析：
为了简化认为气体密度服从波耳兹曼分布
相较前一种情况则需要将

$$B_2$$ 变为:
$$B_2=B_0e^(\frac{-y}{y_0})$$
其中 $$y_0=\frac{k_BT}{mg}=1\times10^4m$$
初始角度为30，45，60时炮弹的轨迹：



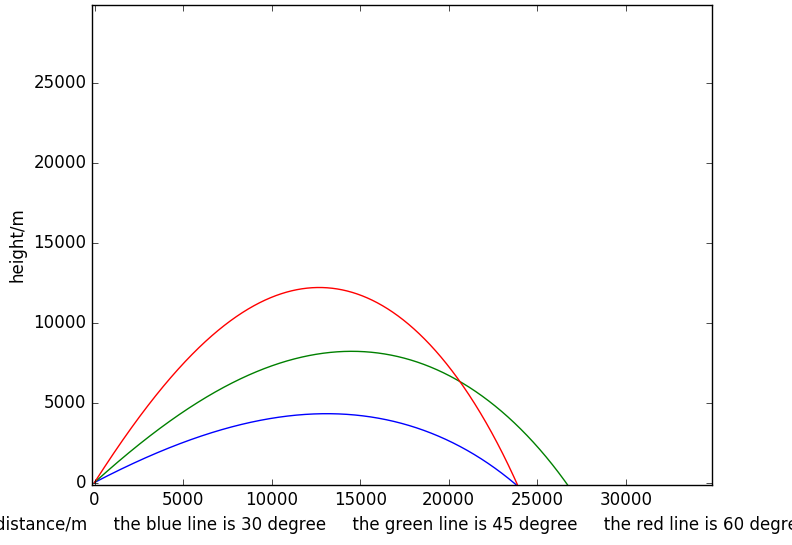
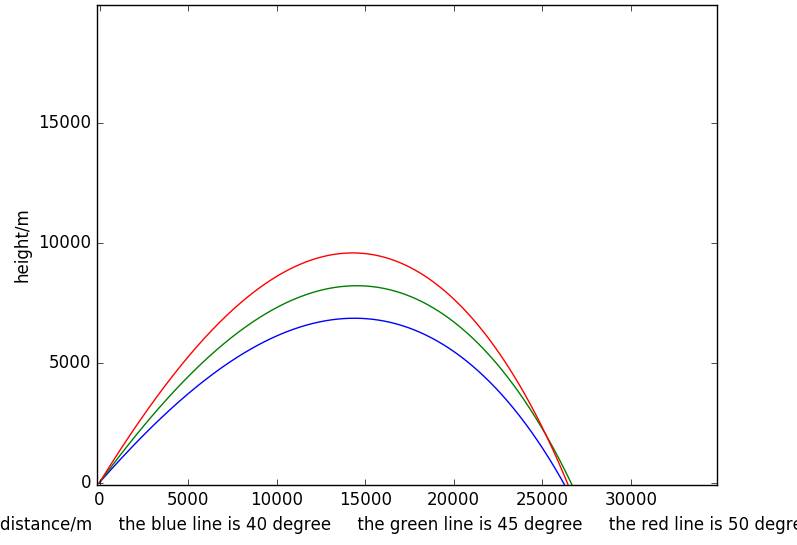
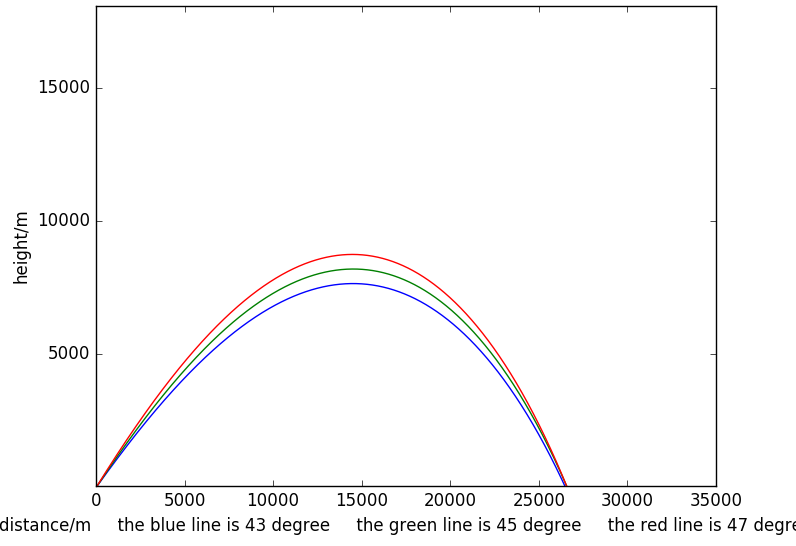
此时炮弹的整体射程小于第一种情况但是大于第二种情况：
将y的取值限定在区间［0，－3]之内给出射程的数值解：

角度／度	射程／米
30	23656.1203
40	26180.4552
43	26512.8946
45	26611.8632
46.5	26618.7672
47	26607.9512
50	26400.5592
60	23820.2634

由以上的表格并且结合物理分析，射程最大的角度出现在45度和47度之间为了提高精度继续细分：

角度／度	射程／米
45.5	26619.5690
46	26621.8973
46.5	26618.7672
45.75	26621.4104
46.25	26621.0196
46.75	26612.9744
45.8	26622.0541
45.9	26623.1768

综上所述：
最大射程的抛射角度45.90度，精确到小数点后一位。

计算程序：

import math
#initial value
t=[]
dt=0.01
M=1.0       #B_2/m=4*10-5 realy count
g=9.8
end_time=100
y_h=0.0001
B_2=4*10**(-5)
a=45.8/180.0*math.pi
b=45.9/180.0*math.pi
c=46.75/180.0*math.pi
theta=[a,b,c] #inital angle 30 45 60
t.append(0)
#print a,b,c
x_1=[]
v_x_1=[]
y_1=[]
v_y_1=[]
x_1.append(0)
y_1.append(0)
v_x_1.append(700*math.cos(theta[0]))  #initial speed equal 700m/s
v_y_1.append(700*math.sin(theta[0]))
for i in range(int(end_time/dt)):
    m=x_1[i]+v_x_1[i]*dt
    x_1.append(m)
    n=v_x_1[i]-(B_2*math.e**(-y_1[i]*y_h))*((v_x_1[i]**2+v_y_1[i]**2)**0.5)*v_x_1[i]*M*dt
    v_x_1.append(n)
    o=y_1[i]+v_y_1[i]*dt
    y_1.append(o)
    p=v_y_1[i]-g*dt-(B_2*math.e**(-y_1[i]*y_h))*((v_x_1[i]**2+v_y_1[i]**2)**0.5)*v_y_1[i]*M*dt
    v_y_1.append(p)
   # print x_1[-1],y_1[-1]
    if o<=0:
       if o>=-3:
          print m,1
x_2=[]
v_x_2=[]
y_2=[]
v_y_2=[]
x_2.append(0)
y_2.append(0)
v_x_2.append(700.0*math.cos(theta[1]))  #initial speed equal 700m/s
v_y_2.append(700.0*math.sin(theta[1]))
for i in range(int(end_time/dt)):
    m=x_2[i]+v_x_2[i]*dt
    x_2.append(m)
    n=v_x_2[i]-(B_2*math.e**(-y_2[i]*y_h))*((v_x_2[i]**2+v_y_2[i]**2)**0.5)*v_x_2[i]*M*dt
    v_x_2.append(n)
    o=y_2[i]+v_y_2[i]*dt
    y_2.append(o)
    p=v_y_2[i]-g*dt-(B_2*math.e**(-y_2[i]*y_h))*((v_x_2[i]**2+v_y_2[i]**2)**0.5)*v_y_2[i]*M*dt
    v_y_2.append(p)
   # print x_2[-1],y_2[-1],
    if o<=0:
       if o>=-3:
         print m,2
x_3=[]
v_x_3=[]
y_3=[]
v_y_3=[]
x_3.append(0)
y_3.append(0)
v_x_3.append(700.0*math.cos(theta[2]))  #initial speed equal 700m/s
v_y_3.append(700.0*math.sin(theta[2]))
for i in range(int(end_time/dt)):
    m=x_3[i]+v_x_3[i]*dt
    x_3.append(m)
    n=v_x_3[i]-(B_2*math.e**(-y_3[i]*y_h))*((v_x_3[i]**2+v_y_3[i]**2)**0.5)*v_x_3[i]*M*dt
    v_x_3.append(n)
    o=y_3[i]+v_y_3[i]*dt
    y_3.append(o)
    p=v_y_3[i]-g*dt-(B_2*math.e**(-y_3[i]*y_h))*((v_x_3[i]**2+v_y_3[i]**2)**0.5)*v_y_3[i]*M*dt
    v_y_3.append(p)
   # print x_3[-1],y_3[-1],
   # if y_3<=0:
      # print(x_3)
    if o<=0:
       if o>=-3:
          print m,3
#draw the picture
import numpy as np
import matplotlib.pyplot as plt
plt.plot(x_1,y_1)
plt.plot(x_2,y_2)
plt.plot(x_3,y_3)
plt.ylabel(u'height/m')
plt.xlabel(u'distance/m     the blue line is 43 degree     the green line is 45 degree     the red line is 47 degree')
plt.title(u"the trial of the cannon")
plt.show()

参考文献：

计算物理教材