homework_7

作者：刘星辰 材料物理专业

背景介绍：

本文主要分析投掷棒球时，棒球的自旋对飞行轨迹的轨迹的影响。首先分析忽略棒球的自旋只考虑空气阻力的影响时棒球的轨迹，最后分析加上自旋以后棒球的轨迹有什么变化。

正文

• 不考虑自旋
  不考虑自旋时棒球的轨迹和homework_6中炮弹的轨迹类似，这里就不再重复。

• 考虑棒球的下旋
  在考虑棒球的下旋运动后，棒球的运动示意图（这是棒球运动的仰视图）如下所示
  
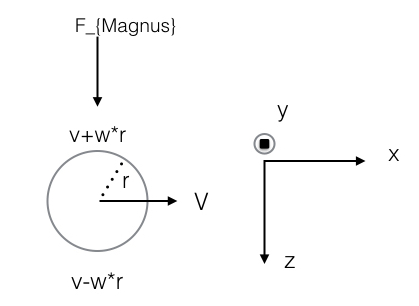
  棒球运动的微分方程与homework_6类似，唯一的区别在于多了一个Z方向的受力:

  $$\vec{F_{Magnus}}=S_0\vec{\omega}\times\vec{v}$$
  棒球运动的微分方程组为：
  $$\frac{dx}{dt}=v_{x}$$ $$\frac{dv_{x}}{dt}=-\frac{B_2}{m}vv_{x}$$ $$\frac{dy}{dt}=v_{y}$$ $$\frac{dv_{y}}{dt}=-g$$ $$\frac{dz}{dt}=v_{z}$$ $$\frac{dv_{z}}{dt}=-\frac{S_{0}v_{x}\omega}{m}$$
  方程中的参数取值如下：
  $$\frac{S_0}{m}=4.1\times10^{-4},\frac{B_2}{m}=0.0039+\frac{0.0058}{1+e^{\frac{v-35}{5}}}$$

• 棒球的自旋对轨迹影响的示意图
  向前初速度取为7m/s，向上初速度取为70m/s时两者的对比图如下所示：
  
  $$分别做出x-y和x-z图像对比$$
  
  

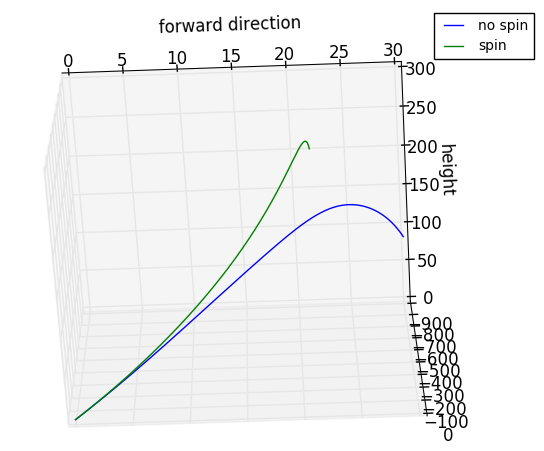
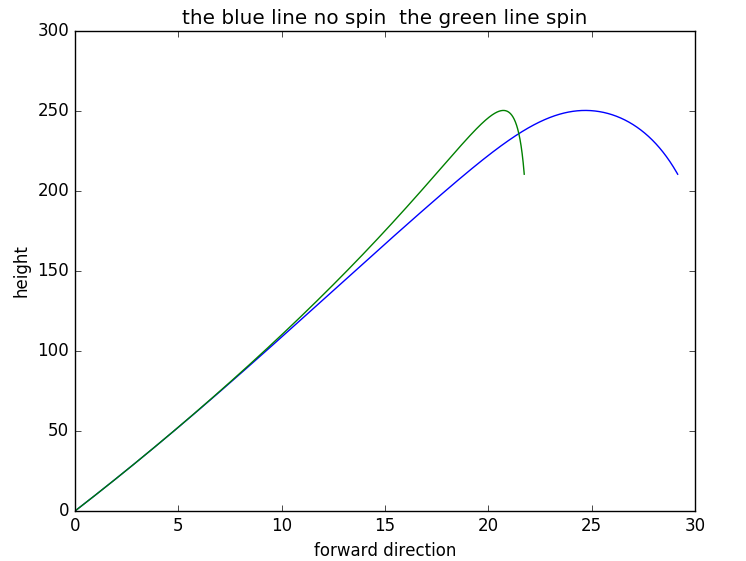
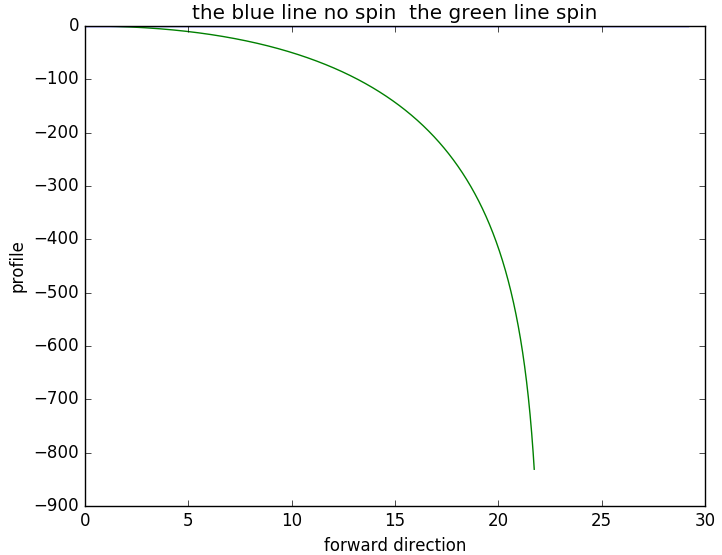
运动参数对比

计算程序:

#coding:utf-8
#initial value
import math
t=[]
dt=0.01    #B/m=4*10-5 realy count
g=9.8
end_time=120
t.append(0)
w=4000*math.pi
v_1=7   #initial volocity
v_2=70
S=4.1*10**-4
#define variable
x_1=[]
v_x_1=[]
y_1=[]
v_y_1=[]
z_1=[]
v_z_1=[]
x_1.append(0)
y_1.append(0)
z_1.append(0)
v_x_1.append(v_1)  #initial speed equal 700m/s
v_y_1.append(v_2)
v_z_1.append(0)
x_2=[]
v_x_2=[]
y_2=[]
v_y_2=[]
z_2=[]
v_z_2=[]
x_2.append(0)
y_2.append(0)
z_2.append(0)
v_x_2.append(v_1)  #initial speed equal 700m/s
v_y_2.append(v_2)
v_z_2.append(0)
#caulate the coordinate
for i in range(int(end_time/dt)):
      d=x_1[i]+v_x_1[i]*dt
      x_1.append(d)
      e=v_x_1[i]-dt*(0.0039+0.0058/(1+math.e**(((v_x_1[i]**2+v_y_1[i]**2+v_z_1[i]**2)**0.5-35)/5)))*((v_x_1[i]**2+v_y_1[i]**2+v_z_1[i]**2)**0.5)*v_x_1[i]
      v_x_1.append(e)
      f=y_1[i]+v_y_1[i]*dt
      y_1.append(f)
      h=v_y_1[i]-g*dt
      v_y_1.append(h)
      z_1.append(0)
      v_z_1.append(0)
      j=x_2[i]+v_x_2[i]*dt
      x_2.append(j)
      p=v_x_2[i]-dt*(0.0039+0.0058/(1+math.e**(((v_x_2[i]**2+v_y_2[i]**2+v_z_2[i]**2)**0.5-35)/5)))*((v_x_2[i]**2+v_y_2[i]**2+v_z_2[i]**2)**0.5)*v_x_2[i]
      v_x_2.append(p)
      l=y_2[i]+v_y_2[i]*dt
      y_2.append(l)
      m=v_y_2[i]-g*dt
      v_y_2.append(m)
      n=z_2[i]+v_z_2[i]*dt
      z_2.append(n)
      o=v_z_2[i]-dt*S*v_x_2[i]*w
      v_z_2.append(o)
#draw the picture
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(x_1, y_1, z_1, label='no spin')
ax.plot(x_2,y_2,z_2,   label='spin')
ax.legend()
plt.show()

参考文献

计算物理教材