@Xc-liu
2016-05-09T15:20:27.000000Z
字数 2161
阅读 1396
homework_11 多星系统
刘星辰
内容简介
正文
- 双星系统的一般分析
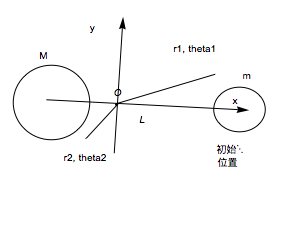
由于没有其它星体的作用,双星系统的质心静止,以双星的质心为坐标原点建立坐标系分析各自相对质心的运动。
分析在时刻的受力
其中
于是的运动学方程为:
同理可得的运动学方程
加上适当的初始条件以后即可得出两个星体的轨道。首先取定两颗星体的初始位置和质量比,(为了与前面的算法匹配,必须使得初始质心坐标为(0,0))。不妨取第一个星体坐标为,质量为,第二个星体质量为,于是第二个星体的坐标必须取为,不同的初速度取值会有不同的轨道。
- 适当的初始条件使得双星系统做圆周运动
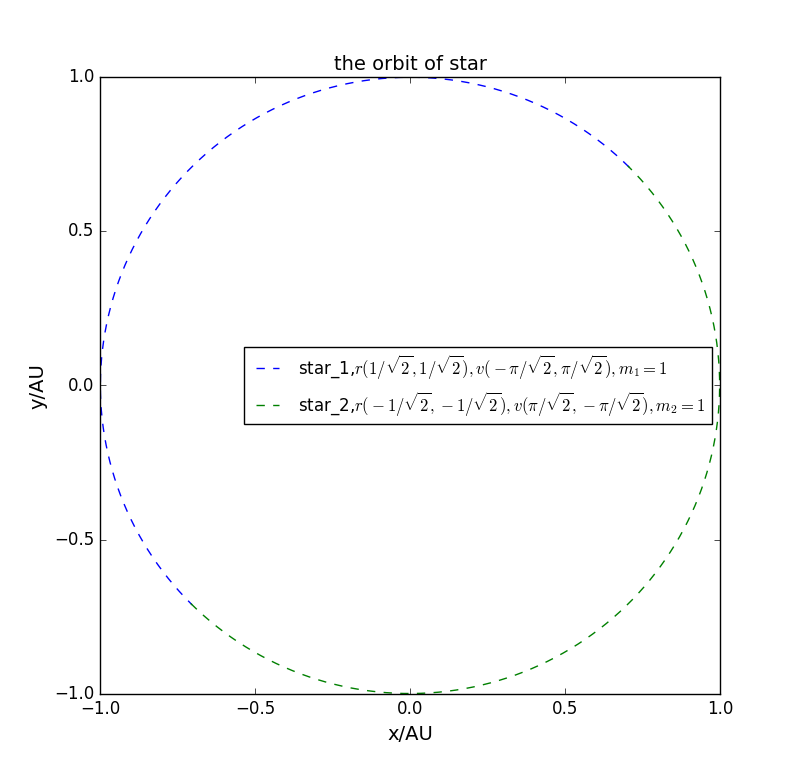
- 选取适当的初始条件使得双星系统做非圆周运动
将初始位置取为质量取为,如果速度取为则正好做圆周运动,如果将初速度增大或者减小相同的值,两者做椭圆运动。
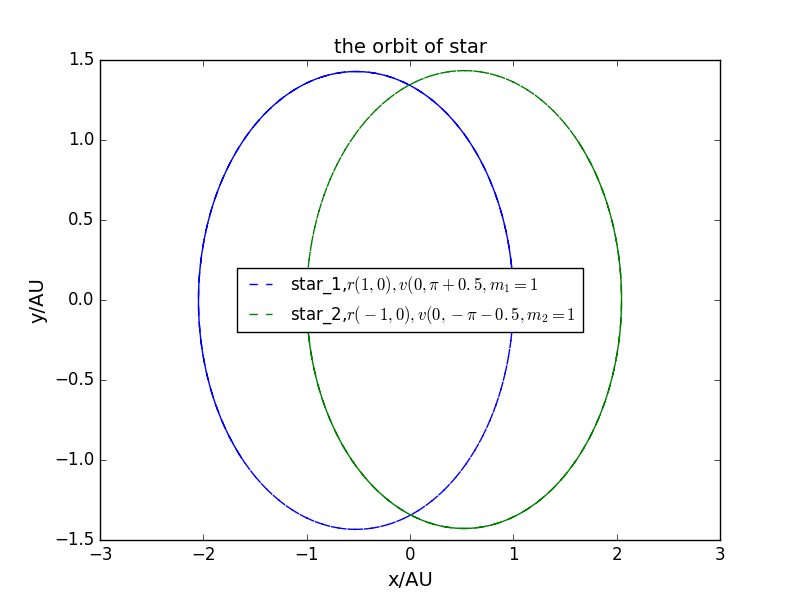
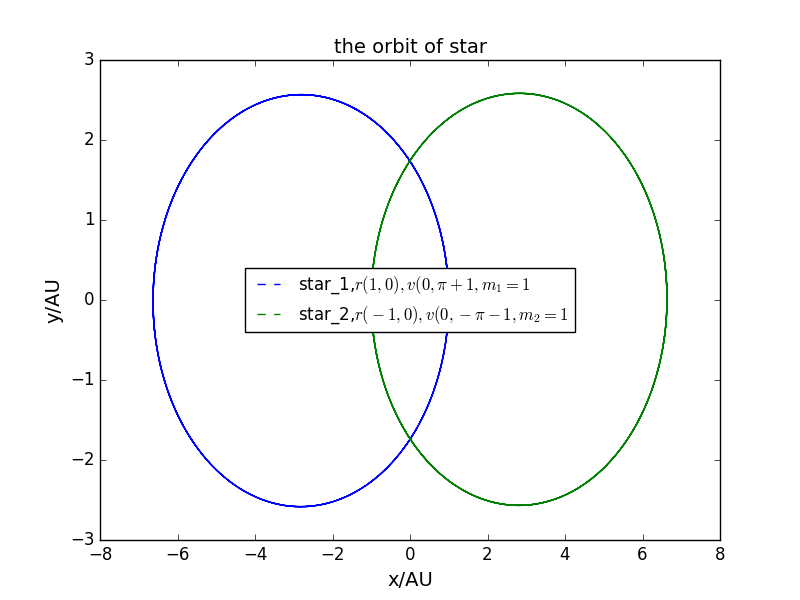
改变的值较大时,轨道会有进动
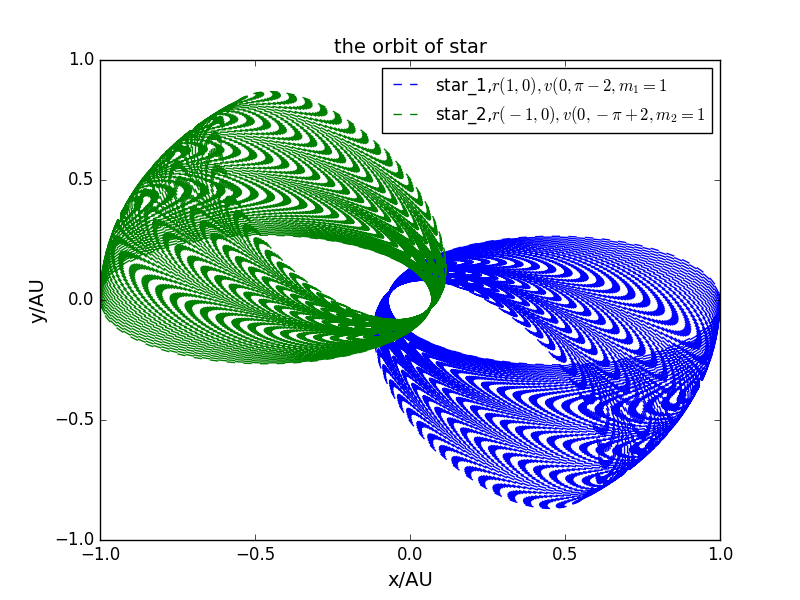
- 改变星体的质量比
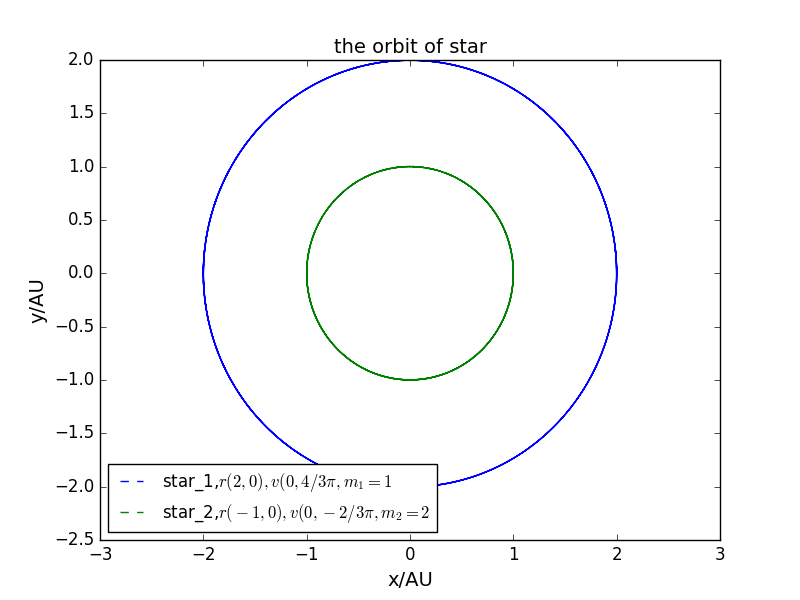
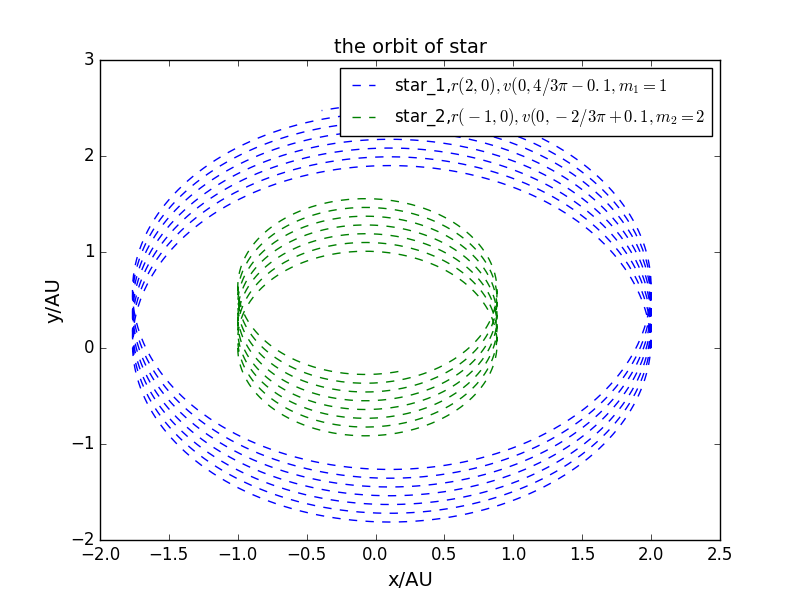
- 双星系统做闭合轨道运动的条件
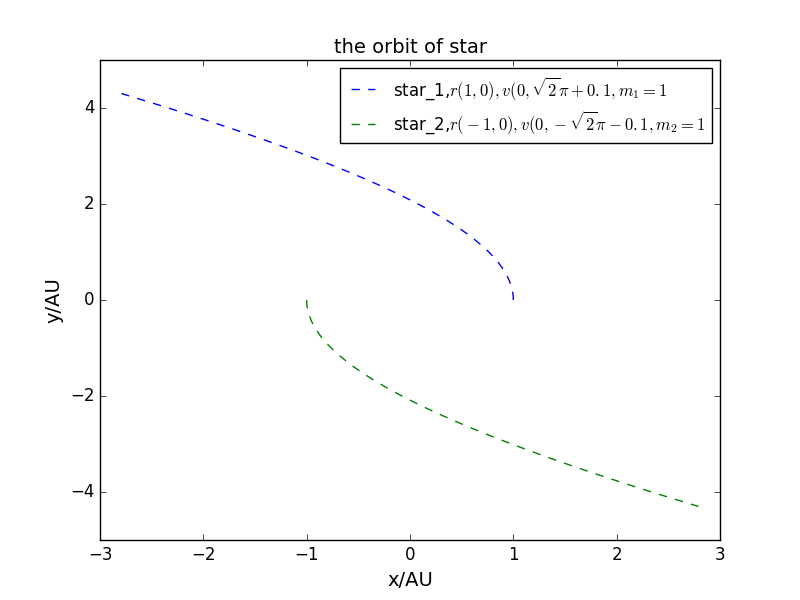
体系中的机械能大于零时轨道将不闭合
时轨道将不闭合,将初始位置取为质量取为,如果速度取为则正好做圆周运动,如果速度改为,恰好取零。
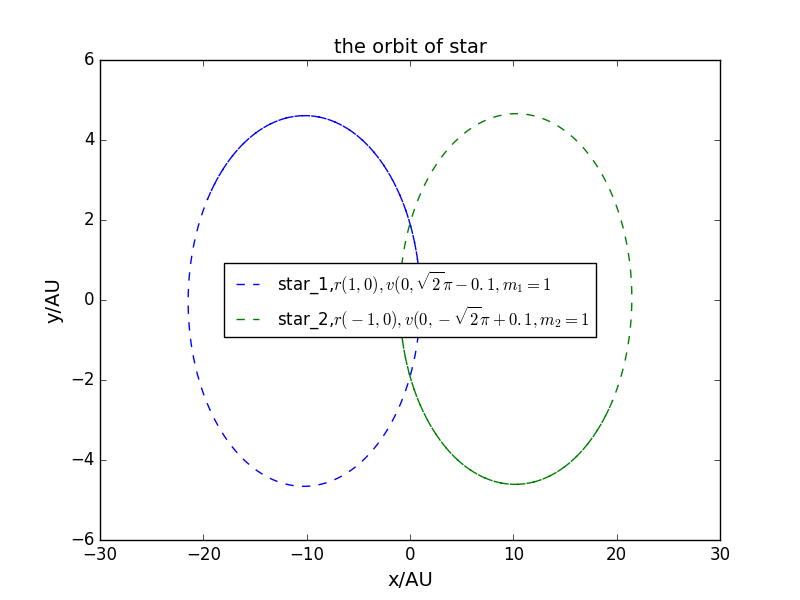
- ()星系统的一般讨论,(n>2时将出现混沌现象)
计算程序2
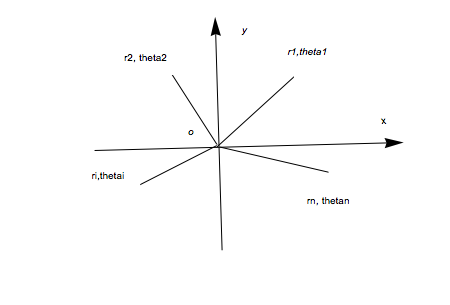
第个星体在时刻的运动方程:
其中
以 为例展示三星系统的混沌现象
选取合适的初始的条件,使得星体做圆周运动。
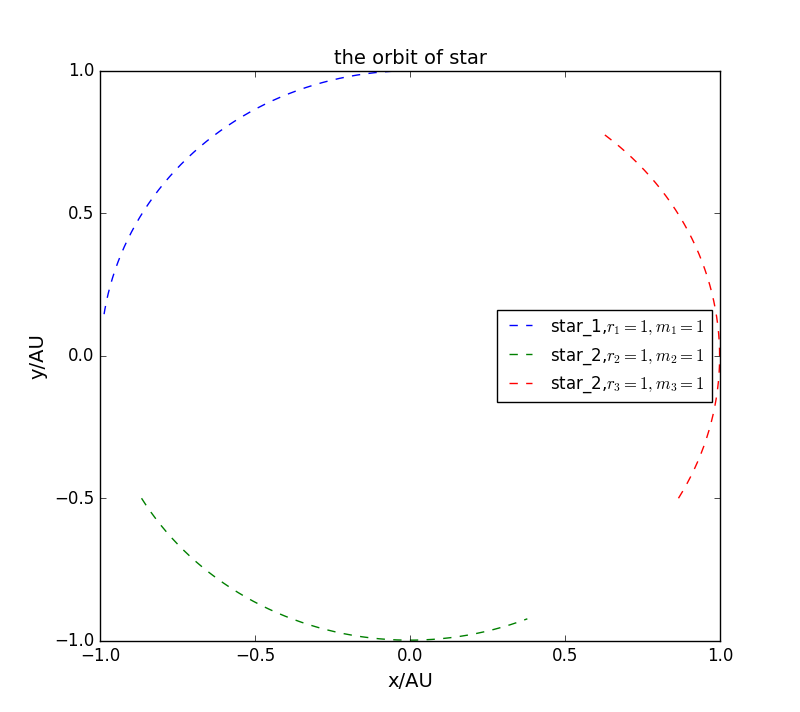
计算时间过长使得误差累计会导致出现混沌。
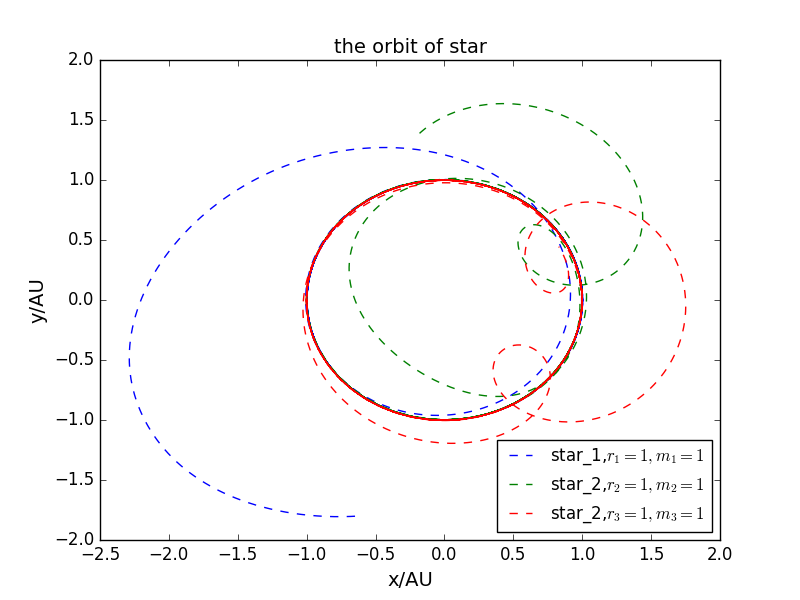
- ()星系统系统的轨道稳定性
星体数目大于三时即出现混沌,轨道很难稳定。但是如果星系中某个星体的质量远远大于其它星体的质量,那么多体问题可以近似的退化为双星体系,这可能是实际星体轨道稳定的原因
总结
随着星系中星体的数目增加,星体的运动规律或许可以利用类似范德瓦尔斯气体状态方程的手段来描述。
参考文献与致谢
感谢陈洋遥同学对计算三星体系程序的修改,以及对旧程序误差分析的帮助。
感谢李明浩同学对轨道稳定性分析的帮助
Computational Physics, Nicholas J. Giordano & Hisao Nakanishi
How to think like a computer scientist -- Learning with Python: Interactive Edition 2.0
