homework_8

作者：刘星辰

内容简介：

本文主要分析非简谐振动的周期与非简谐力之间的的具体关系，并且比较不同的数值计算方法的计算精度。具体地，有Euler methond,Euler-cromer methond,Runge-Kutta methond。本文给出了课本习题3—4，3—5的解答。

周期的解析表达式：

非简谐运动的运动微分方程：

$$\frac{d^{2}x}{dt^{2}}=-kx^{\alpha}$$
给定运动过程中的最大位移为:
$$x_{m}$$
则运动周期的解析解为：
$$T=4\sqrt{\frac{\alpha+1}{k}}\int_{0}^{x_m}{((x_m)^{\alpha+1}-(x)^{\alpha+1}})^{-\frac{1}{2}}dx$$
特别地：
$$\alpha=1,T=2\pi\sqrt{\frac{\alpha+1}{k}}$$ $$\alpha为其它数值时周期T将会与最大位移x_m相关$$
周期具体的解析解可以参考陈洋遥同学给出的结论。

不同数值计算方法比较：

以二阶常微分方程为例比较不同算法的计算结果，同时验证程序的正确性。

$$\frac{d^{2}x}{dt^{2}}=-x,x(0)=1,x^{'}(0)=0$$
可很容易得到方程的解析解为：
$$x(t)=cos(t)$$
利用Euler methond，Euler-cromer methond,Runge-Kutta方法分别计算：

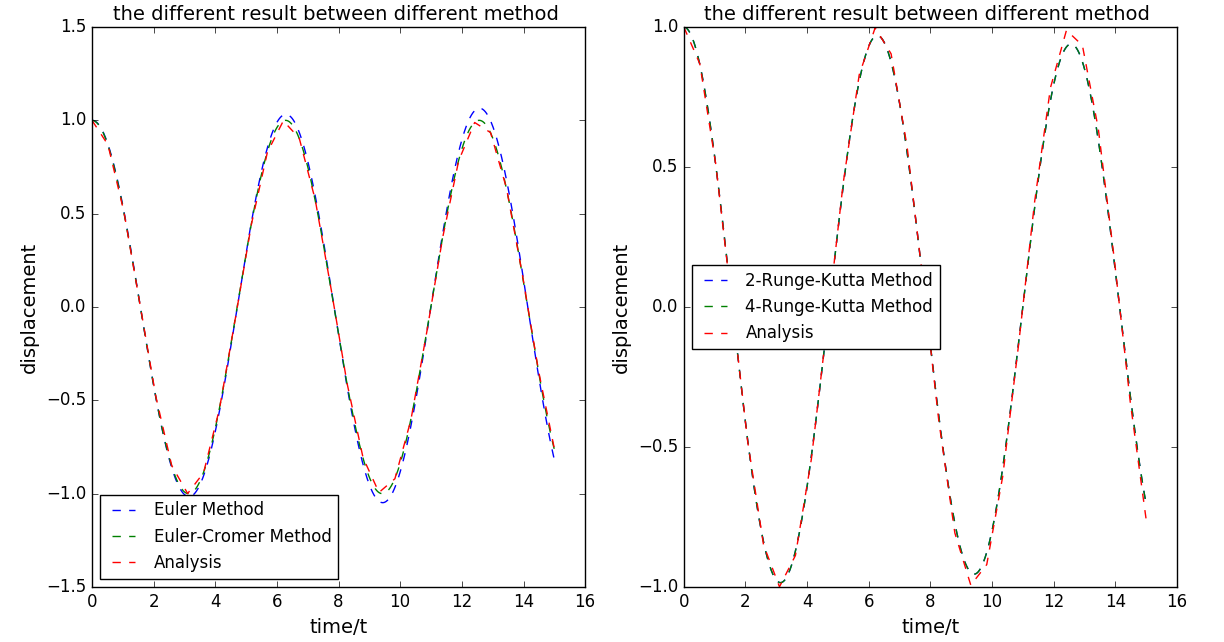
具体的计算程序_1

非简谐运动的分析：

非简谐运动的运动微分方程：

$$\frac{d^{2}x}{dt^{2}}=-kx^{\alpha}$$
下面采用四阶R—K算法计算其数值解，在参数的取值：
$$k=1,\alpha=1,2,3$$
计算得出的运动图像：

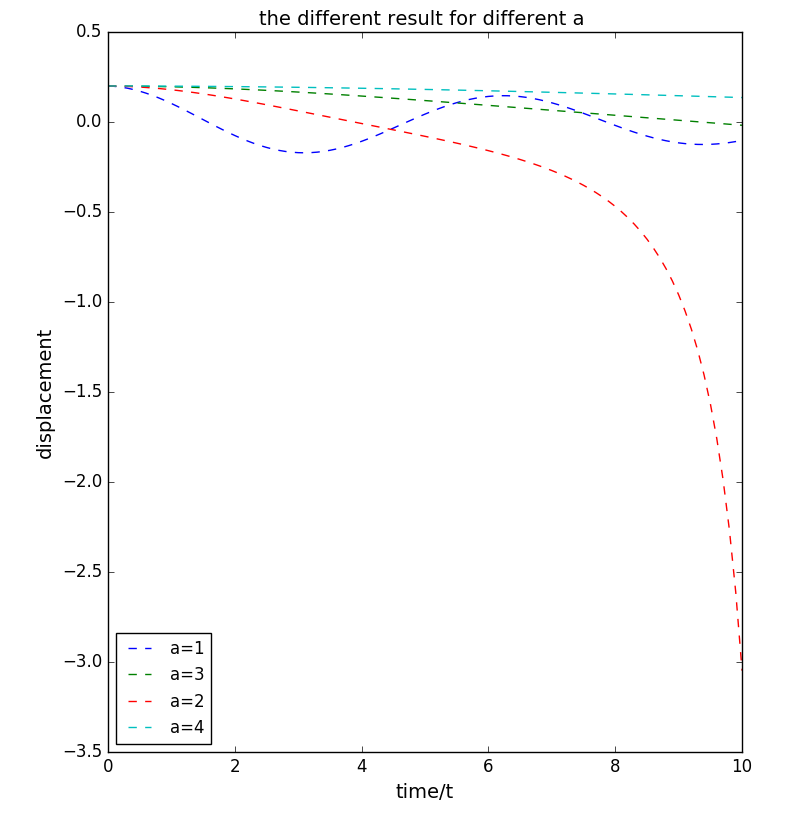
具体的计算程序_2
从运动图像可以大致看出：
$$当\alpha=1,3时运动是稳定的，\alpha为其它值时运动偏离平衡位置后不能复原$$
$$利用周期的解析表达式计算不同振幅不同\alpha下运动周期的变化。$$
运动周期表达式为：
$$T=4\sqrt{\frac{\alpha+1}{k}}\int_{0}^{x_m}{((x_m)^{\alpha+1}-(x)^{\alpha+1}})^{-\frac{1}{2}}dx$$
首先利用一个例子检验积分的数值计算程序的精度
$$\int_{0}^{1}{x}dx=\frac{1}{2}$$
当步长dx取为0.0001时计算结果为0.49995，误差为0.05%。
计算周期时参数的取值情况如下：
$$k=1$$

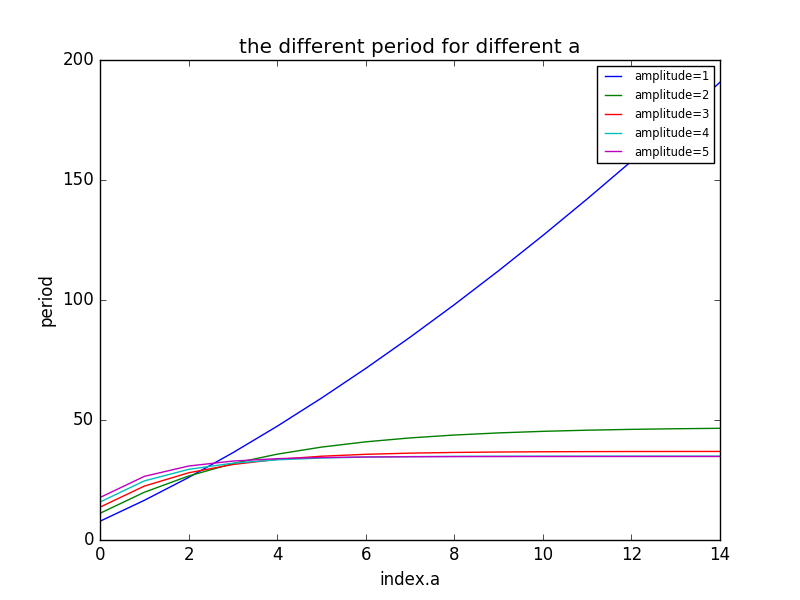
具体的计算程序_3
曲线在a=2时周期与振幅无关这与理论预测吻合，但是在a>2,相同的a时振幅大的周周期反而小，我对这一点有疑问。

致谢：

• 本文的计算和绘图（除运动周期的算法）全部借鉴陈洋遥大神的程序
• 最后一个图感谢李明浩同学的帮助
• 参考书目计算物理教材