极性液体膜在外加电场下的转动

计算物理
刘星辰—2013301020167—材料物理—计算物理期末论文

---

背景介绍

将液体膜置于一个平行板电容器中($\vec{E_{ext}}$)，同时在液体表面加一个表面电流($\vec{J_{cur}}$)。这样就会使得液体膜旋转。本人曾于2015年和李明浩，陈洋遥合作做过这个实验，当时通过相机记录转动情况。基于流体力学中动量流的的概念，本人提出了一个液体膜转动的理论模型。 当时受限于数值计算能力的限制，没能很好的将理论和实验数据对比。

---

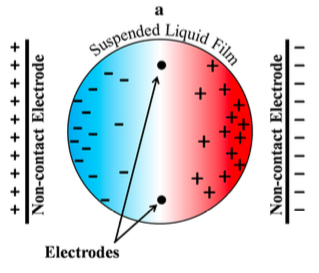
液体膜转动的理论模型

---

电容器在液体膜中产生的电场

电容器产生的电场大小为$E_{ext}=\frac{U_{ext}}{d}$,(不考虑边缘效应.)。电容产生的电场使得液膜极化，且极化强度为$\vec{p}=\frac{(\varepsilon _{r}-1)\varepsilon _0}{\varepsilon _{r}}\vec{E_{ext}}$。在液膜边缘出现极化电荷，极化电荷产生一个退极化场其大小为$\vec{E^{'}}=-\frac{\vec{p}}{\varepsilon _0}=\frac{(\varepsilon _{r}-1)}{\varepsilon _{r}}\vec{E_{ext}}$。考虑到水的相对介电常数大约为$80$，则退极化场对外场有很大程度抵消。因此$E_{ext}$的作用是将液膜极化并且大致固定偶极子的方向，但是不会对其有力矩的作用。

---

外加电流在水中产生的电场

假定导线的电导率为$\sigma_{'}$,液体的电导率为$\sigma$,以正电极为例利用静电场高斯定理有:

$$q=\varepsilon _0\int{\vec{E}\cdot d\vec{s}}=\varepsilon _0(\frac{1}{\sigma^{'}}\int{\vec{J^{'}}\cdot d\vec{s^{'}}}+\frac{1}{\sigma^{}}\int{\vec{J^{}}\cdot d\vec{s^{}}})=\varepsilon _0(-I/\sigma_{'}+I/\sigma)$$
考虑到一个事实导线的电导率远大于液体的电导率，则:
$$q=\varepsilon _0I/\sigma$$
同理可得负极的积累的电荷为：
$$q=－\varepsilon _0I/\sigma$$
至此就可以知道外加电流在水中产生的电场等效于两个电量为$q$的异种电荷产生的场。（其它位置也有电荷分布，两个点电荷是等价处理。)

---

液体转动原因的定性说明

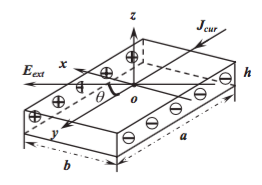
外加电场使得液膜极化，液膜其中的偶极子受到外加电流产生的场的力矩作用，在力矩的作用下液体膜发生转动。对于单个偶极子而言其受到的力矩大小为：

$$\vec{M}=\vec{p}\times\vec{E_{cur}}$$
单位质量的质元受到的力矩大小为:
$$\vec{M}=\frac{\Delta m}{\rho}\vec{p}\times\vec{E_{cur}}$$
其中$\rho$为液体膜的密度。
显然，力矩的大小与$\vec{p}$和$\vec{E_{cur}}$的夹角相关。但时考虑到一个事实$\vec{E_{cur}}<<\vec{E_{ext}}$,故$\vec{E_{ext}}$与$\vec{E_{cur}}和\vec{E_{ext}}$的矢量和$\vec{E}$的夹角很小。因此$\vec{p}$和$\vec{E_{cur}}$的夹角可以近似认为不变。具体地，偶极子在$\vec{E}$附近做微振动，振动方程为：
$$\frac{d^2\theta}{dt^2}I=-pEsin\theta$$
其中，$I$为偶极子的转动惯量，更进一步在小角近似下,$sin\theta =\theta$,由此可以计算出振动的圆频率：
$$\omega=\sqrt{\frac{pE}{I}}$$
通过估算圆频率$\omega$的数量级为$10^{12}Hz$,其辐射产生的磁场的数量级为$10^{-16}T$,辐射产生的电场的数量级为$10^{-24}V/m$, 考虑到$\vec{E_{cur}}$和$\vec{E_{ext}}$的数量级，偶极子的电磁辐射可以忽略。

---

利用“角动量扩散模型”定量描述液膜的转动

液膜的转动可以视为一系列同心圆环的转动，每个同心圆环的转动角速度不相同。角速度大的圆环会把角动量转移给角速度小的圆环，这样在不同的圆环之间就会有一个角动量流。同时外场产生的力矩$M(x,y)$会向圆环输入角动量，相当于一个源。这种角动量的输运在液体中主要是由于分子之间的相互吸引造成的宏观效果。
类似热量的流动（傅里叶定律），分子浓度的扩散（费克定律），单位时间通过单位面积的角动量正比于角速度的下降率，即:

$$l=-k\bigtriangledown\omega$$
下面来说明做这样类比的合理性。如图所示:

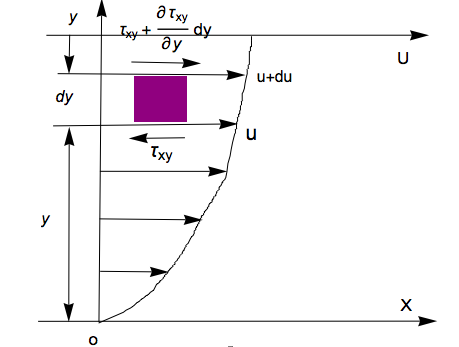
图示的横纵坐标轴为流体所在的位置坐标，由于$y$ 坐标的不同流体的速度不同，向右的箭头的大小正比与速度的大小。
由于速度的不同在$y$和$y+dy$ 这两层之间产生一个应力。由牛顿内摩擦定律：
$$\tau=\mu\frac{dv}{dy}$$
则有：
$$y\tau=y\mu\frac{dv}{dy}=\mu(\frac{dvy}{dy}-v)$$
考虑到一个事实，$\frac{dv}{dy}>>v/y$,（实验上速度随y变化很大，这是力矩随y变化很大导致，如果不满足这个近似，会导致扩散方程的非线性化。）
$$y\tau=y\mu\frac{dv}{dy}=\mu\frac{dvy}{dy}=M_{\tau}$$
由$l=-k\bigtriangledown\omega$ 具体化：
$$\frac{\Delta m\omega}{\Delta t}\frac{1}{\Delta x \Delta y}=-k\frac{d\frac{\Delta m\omega}{\Delta V}}{\Delta y}=-k\rho \frac{d\omega}{dy}$$
由此可知：
$$k=-\frac{\rho}{\mu}$$
也就是说定义的常数$k$可以与已知的常数联系起来！同时这也说明以上假设的合理性。
据此很容易推导出角速度的扩散方程：
$$\frac{\partial\omega}{\partial t}=M(x,y)+D\triangle\omega$$
其中$D=\frac{k}{\rho}$,$M(x,y)=\frac{(\varepsilon_r-1)\varepsilon_0}{\rho\varepsilon_r}\cdot E_{ext}E_{cur}sin\theta$
在交流的情况下，$M(x,y)=\frac{(\varepsilon_r-1)\varepsilon_0}{\rho\varepsilon_r}\cdot E_{ext}E_{cur}sin\theta cos^2(wt+\alpha)$

• 考虑到摩擦损耗：

$M(x,y)$可以修改为$M(x,y)-f\cdot r$,这里$f＝k_0\cdot \omega r$

---

利用数值计算方法计算膜的运动情况

选取圆形边界，且边界条件取为：

$$\omega(0.\theta,t)=\omega(a,\theta,t)=0$$
在极坐标中给出方程的形式：
$$\frac{\partial\omega}{\partial t}=M(r,\theta)+D\triangle\omega$$
此时$\Delta$的形式为：
$$\Delta=\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})+\frac{1}{r^2}\frac{\partial^2}{\partial\theta^2}$$
其中：
$$M(r,t)=E_{ext}\cdot q(\frac{1}{(r-a(1+\epsilon))^2}+\frac{1}{(r+a(1+\epsilon))^2})sin^2(wt)-fr$$
方程的离散化[1]
$$\frac{\omega(i,n)-w(i,n-1)}{\Delta t}=M(i,n-1)+$$ $$D\frac{1}{r(i)}\frac{\omega(i,n-1)-w(i-1,n-1)}{\Delta r}+D\frac{\omega(i+1,n-1)+w(i-1,n-1)-2\omega(i,n-1)}{\Delta r^2}$$
整理后得到：
$$\omega(i,n)=w(i,n-1)+\Delta tM(i,n-1)+$$ $$(\omega(i,n-1) -\omega(i-1,n-1))\cdot\alpha_1/r(i)+\alpha_2(\omega(i+1,n-1)+w(i-1,n-1)-2\omega(i,n-1))$$
其中：$\alpha_1=D\Delta t/\Delta x,\alpha_2=D\Delta t/\Delta x^2,M=\frac{(\varepsilon_r-1)\varepsilon_0}{\rho\varepsilon_r}\cdot E_{ext}E_{cur}sin\theta sin^2(wt+\alpha)-fr$

• 参数取值

$$扩散系数D=\frac{1}{\mu}=0.1\times\frac{1}{Pa\cdot s},圆环半径a=1m$$ $$E_{ext}=1\times10^3V/m,摩擦系数k_0=10^{-3},q=－\varepsilon _0I/\sigma=1\times10^{-3}C$$

• 计算结果分析

在直流情况下如果将边界条件和初始条件取为如下形式：

$$w(a,t)=0,w(0,t)=为有限值，w(x,0)=0$$

fig-1,交流情形下w=0.3，速度场的稳态分布t=10, 位置坐标的单位为/10cm,速度条的单位0.1mm/s.

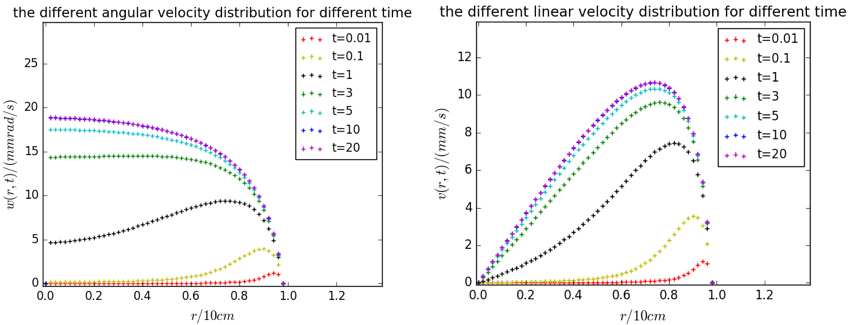
fig-1,直流情况下速度分布随时间变化
初始时刻角速度的极大值出现在边界附近，这是由于初始时摩擦阻力远小于驱动力，而且边界附近的驱动力较大导致的结果。随着时间的推移，速度增加阻力增大，角速度的极大值开始向中间移动， 大概在t=10时达到稳态分布。

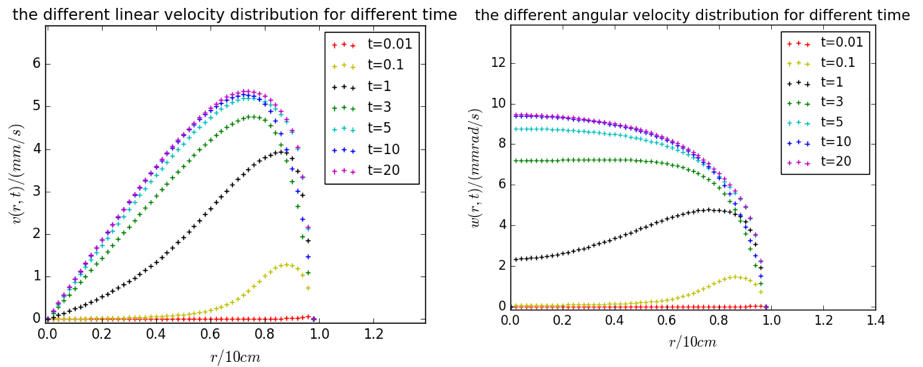
fig-2,在交流情况下速度分布随时间的变化,角频率w=40
在频率较高的交流情形下，角速度和线速度的变化趋势和直流情形大致相同，区别在于：1.速度的数值大概为原来的一半，2.达到平衡的时间微小增加。第一点变化可以给出定性的分析，由于交流频率较高，任意运动时间都可以大致认为时交流周期的整数倍。考虑交流情形下的驱动项:

$$M=mcos^2(wt+\theta)$$
对时间取平均：
$$\overline{M}=\int^{T}_{0}mcos^2(wt+\theta)dt=m/2$$

• 当交流电角频率大致与转动角频率相当时的现象

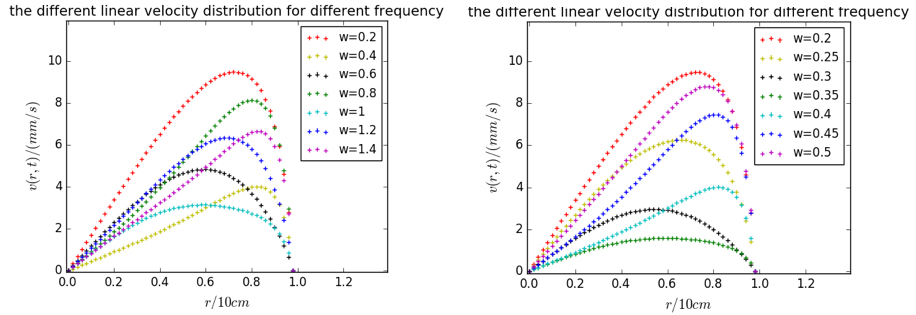
fig-3,频率的改变对速度稳态分布t=10的影响
从图中可以明显看出，线速度分布对于$(0.1,1)$范围内的角频率变化非常敏感。大约在$w=0.2$时线速度分布值明显大于其它情况。可以认为这个频段发生了共振现象。

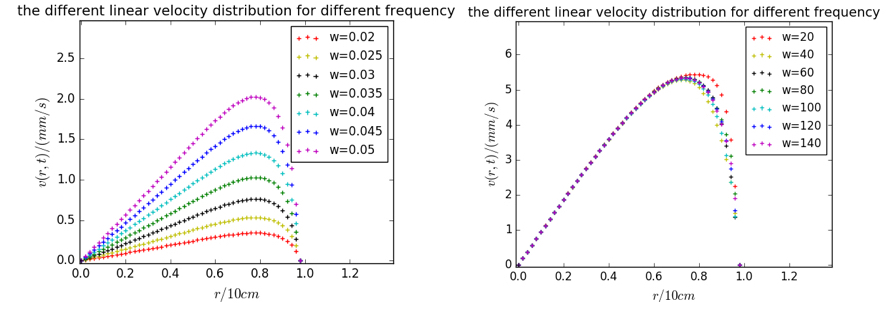
fig-4, 其它频段的频率改变对速度稳态分布t=10的影响
通过以上两图可以看出速度分布对其他频段的交流电并不敏感。

---

总结

通过数值计算的分析结果，可以得出在外加电场和表面电流作用下的液体膜转动的基本特点：
1,液体膜的转动的角速度扩散的宏观方向是由边缘到中心。
2,液体膜的线速度和角速度的径向分布随时间变化，最终达到稳定分布。线速度的极大值出现位置随时间由边缘向中心推移，最终稳定在中间某处，角速度的极大值出现位置随时间由边缘向中心推移，最终稳定在正中心。
3,如果表面电流为交流电，速度分布达到稳态的时间变长，而且 在高频时速度的大小变为直流时的一半左右。在某一频段$(0.1,1)$内，速度分布对交流电频率非常敏感。大约在$w=0.2$ 时发生共振。

---

计算程序

1:
from numpy import *
import math
import matplotlib.pyplot as plt
import numpy as np
import pylab as pl
##########
def ploy(t_t,cmd,cme):
    D=10**-1
    a=1
        w0=40
    E_e=10**3
    q=10**-3
    k0=1*10**-3
    #########
    w_bf=[]
    w_nw=[]
    x=[]
    t=[0]
    dx=0.02
    e=dx
    dt=0.001
    a_1=D*dt/dx
    a_2=D*dt/dx**2
    l=int(a/dx)
    ############
    for i in range(int(a/dx)):
        x.append(0+i*dx)
        w_bf.append(0)
        w_nw.append(0)
    ############
    for k in range(int(t_t/dt)):
        for i in range(int(a/dx)):
        #M=E_e*q*(1.0/(x[i]-a*(1+e))**2+1.0/(x[i]+a*(1+e))**2)*(math.sin(w0*(t[0]+(k-1)*dt)))**2
        M=E_e*q*(1.0/(x[i]-a*(1+e))**2+1.0/(x[i]+a*(1+e))**2)
        print w_nw[3]
        if i==0:
           w_nw[i]=0
        if i==l-1:
           w_nw[i]=0
        if i>0:
           if i<l-1:
              w_nw[i]=w_bf[i]+dt*(M-k0*x[i]*w_bf[i]*x[i])+(w_bf[i]-w_bf[i-1])*a_1/x[i]+a_2*(w_bf[i+1]+w_bf[i-1]-2*w_bf[i])
        for j in range(int(a/dx)):
        w_bf[j]=w_nw[j]
    for m in range(int(a/dx)):
        w_nw[m]=x[m]*w_nw[m]
    ##########
    plt.scatter(x,w_nw,marker='+',color=cmd,label=cme)
    plt.title(u'the different linear velocity distribution for different time',fontsize=14)
    plt.xlabel(u'$r/10cm$',fontsize=14)
    plt.ylabel(u'$v(r,t)/(mm/s)$',fontsize=14)
    plt.legend(fontsize=12,loc='best')
ak=[0.01,0.1,1,3,5,10,20]
cmd=['r','y','k','g','c','b','m']
cme=['t=0.01','t=0.1','t=1','t=3','t=5','t=10','t=20']
for i in range(7):
    ploy(ak[i],cmd[i],cme[i])
plt.show()
2:
import numpy as np
import matplotlib.pyplot as plt
Y, X = np.mgrid[-1:1:20j, -1:1:20j]
U=-(((X**2+Y**2)**0.5-0.5)**2+2.5)*Y/(X**2+Y**2)
V=(((X**2+Y**2)**0.5-0.5)**2+2.5)*X/(X**2+Y**2)
#U=-Y/(X**2+Y**2)**0.5
#V=X/(X**2+Y**2)**0.5
speed=np.sqrt(U*U+V*V)
print speed
fig0, ax0 = plt.subplots()
strm = ax0.streamplot(X, Y, U, V, color=U, linewidth=2, cmap=plt.cm.autumn)
fig0.colorbar(strm.lines)
fig1, (ax1, ax2) = plt.subplots(ncols=2)
ax1.streamplot(X, Y, U, V, density=[0.5, 1])
lw =10*speed/speed.max()
ax2.streamplot(X, Y, U, V, density=0.6, color='k', linewidth=lw)

---

参考文献

---