homework_9 单摆中的混沌现象

目录:

内容简介

本文主要讨论非线性有耗散和驱动力的摆中出现的混沌现象。验证适当的情形下，初始条件的改变会导致结果的巨大变化。更进一步，在相空间中观测混沌现象，分析初始条件对Poincare Section和strange attractor的影响。通过计算体会混沌过程与随机过程的区别，从而理解混沌的准确含义。

正文

本文主要分析非线性耗散摆中的混沌现象，体系运动的微分方程可以比较简单的给出：

$$\frac{d^{2}\theta}{dt^{2}}=-\frac{g}{l}sin(\theta)-q\frac{d\theta}{dt}+F_{D}sin(\Omega_{D}t)......(9-1)$$ 方程中$\frac{g}{l}sin(\theta)$ 体现重力的影响，$q\frac{d\theta}{dt}$体现耗散力的影响，$F_{D}sin(\Omega_{D}t)$体现周期性驱动力的影响，当$F_{D}$取适当的值时体系会出现混沌现象即运动显得杂乱无章。（9-1）式很难给出解析解，下面将利用euler_cromer方法在适当的初始条件下给出数值解。

混沌摆的基本特征

在不同的初始条件下，利用euler_cromer方法给出方程（9-1）的数值解。计算程序为homework_9_1

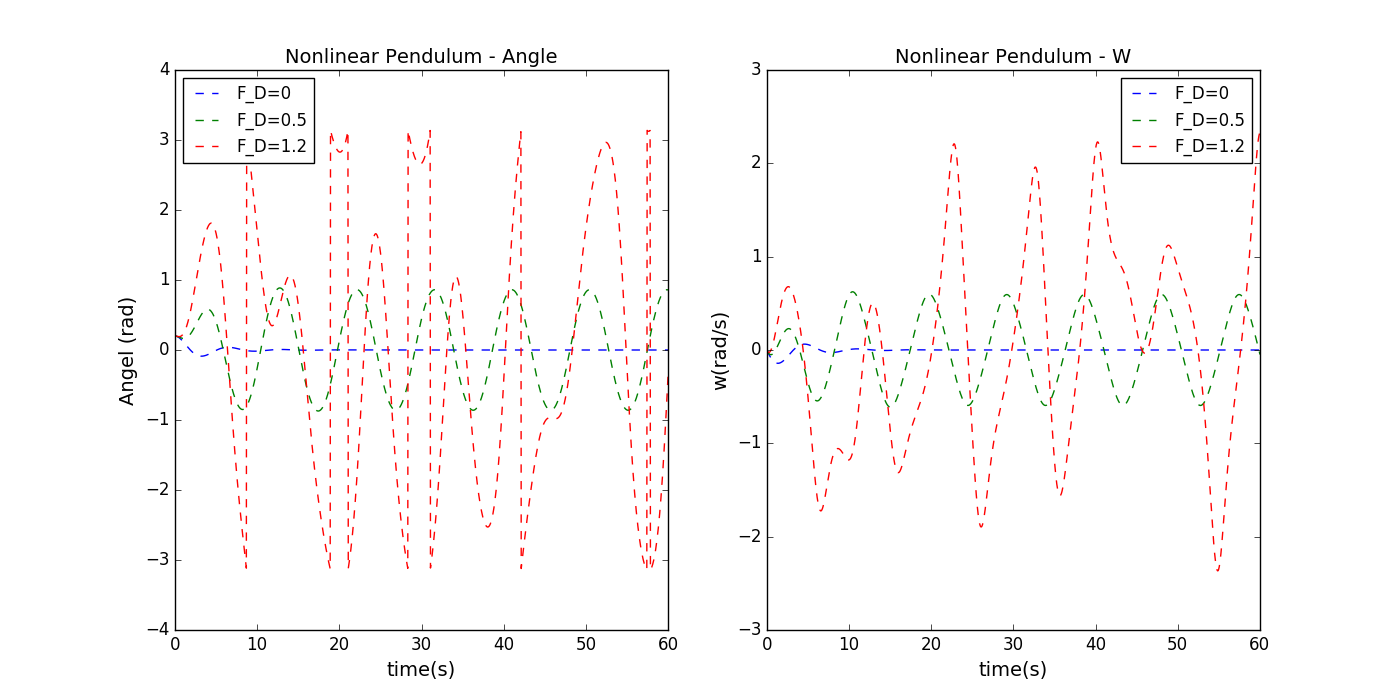
FIGURE 9.1

• 左图显示了在不同振幅的周期性驱动力作用下，转角随时间变化的图像。右图显示了不同振幅的周期性驱动力作用下，角速度随时间变化的关系图像。其中参数的取值为:$F_{D}=0,0.5,1.2;q=1/2,\Omega_{D}=2/3,dt=0.04;\theta(0)=0.2;\omega(0)=0$
  所有参数的单位均为国际单位。

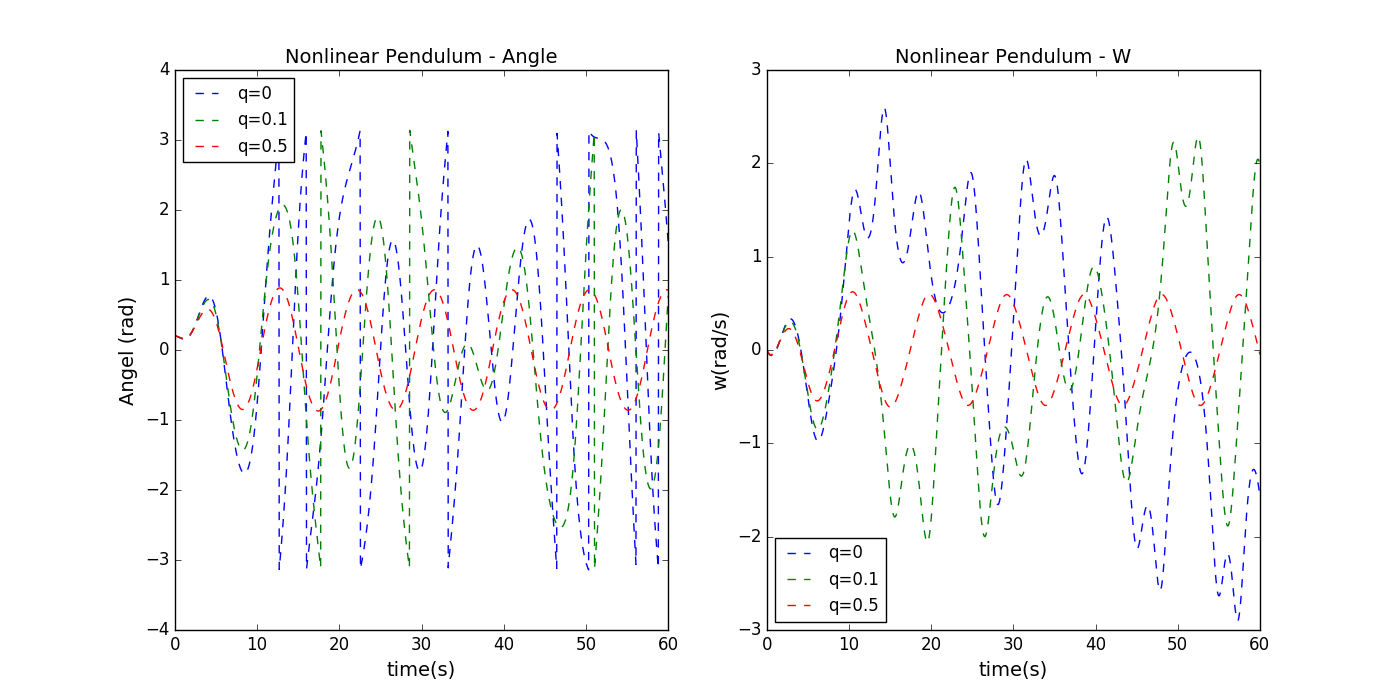
FIGURE 9.2

• 左图显示了在不同大小的耗散力作用下，转角随时间变化的图像。右图显示了不同大小的耗散力作用下，角速度随时间变化的关系图像。其中参数的取值为:$F_{D}=0,0.5,1.2;q=1/2,\Omega_{D}=2/3,dt=0.04;\theta(0)=0.2;\omega(0)=0$
  所有参数的单位均为国际单位。

从上面两幅图分析可以得出：出现混沌现象时运动的周期性逐渐消失；驱动力的振幅的振幅增加会使体系趋向出现混沌；耗散阻力系数q的减小会到导致体系趋于出现混沌现象。

初始条件对混沌体系的影响示意图
计算程序为homework_9_2


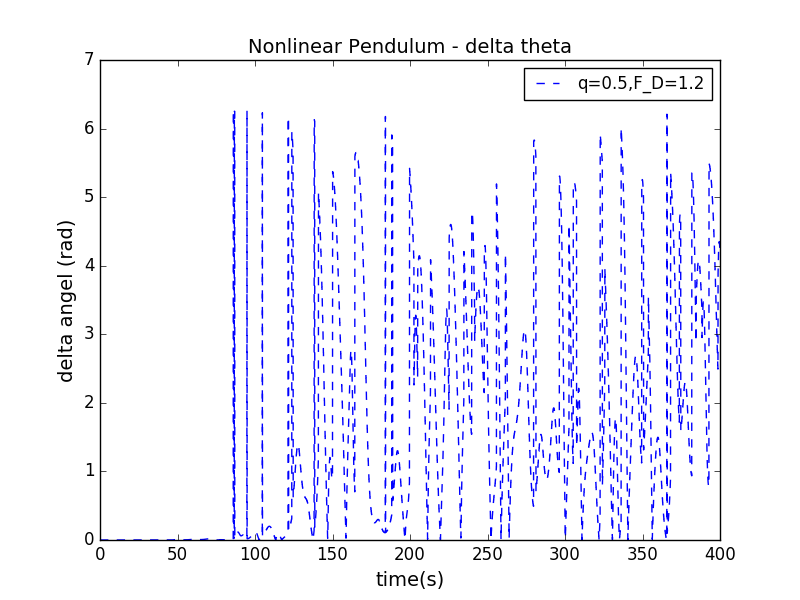
FIGURE 9.2

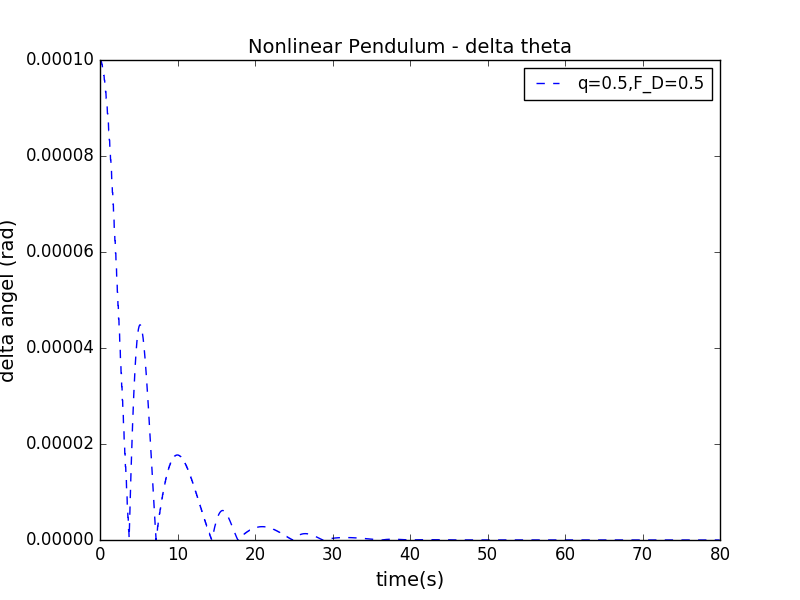
FIGURE 9.3

• 上图显示了在初始的角度$\theta_{0}$相差0.001的情形下，转角的差值随时间变化的图像，此时驱动力振幅$F_{D}=1.2$。下图显示了在初始的角度$\theta_{0}$相差0.001的情形下，角速度随时间变化的关系图像，此时驱动力振幅$F_{D}=0.5$。其中参数的取值为:$q=1/2,\Omega_{D}=2/3,dt=0.04;\theta(0)=0.2;\theta^{'}(0)=0.2001;\omega(0)=0$
  所有参数的单位均为国际单位。

上面两幅图说明驱动力较大时才会使得误差随时间变化而增大

不同观测时刻下的Poincare Section

首先分析在相空间中混沌摆的运动图像

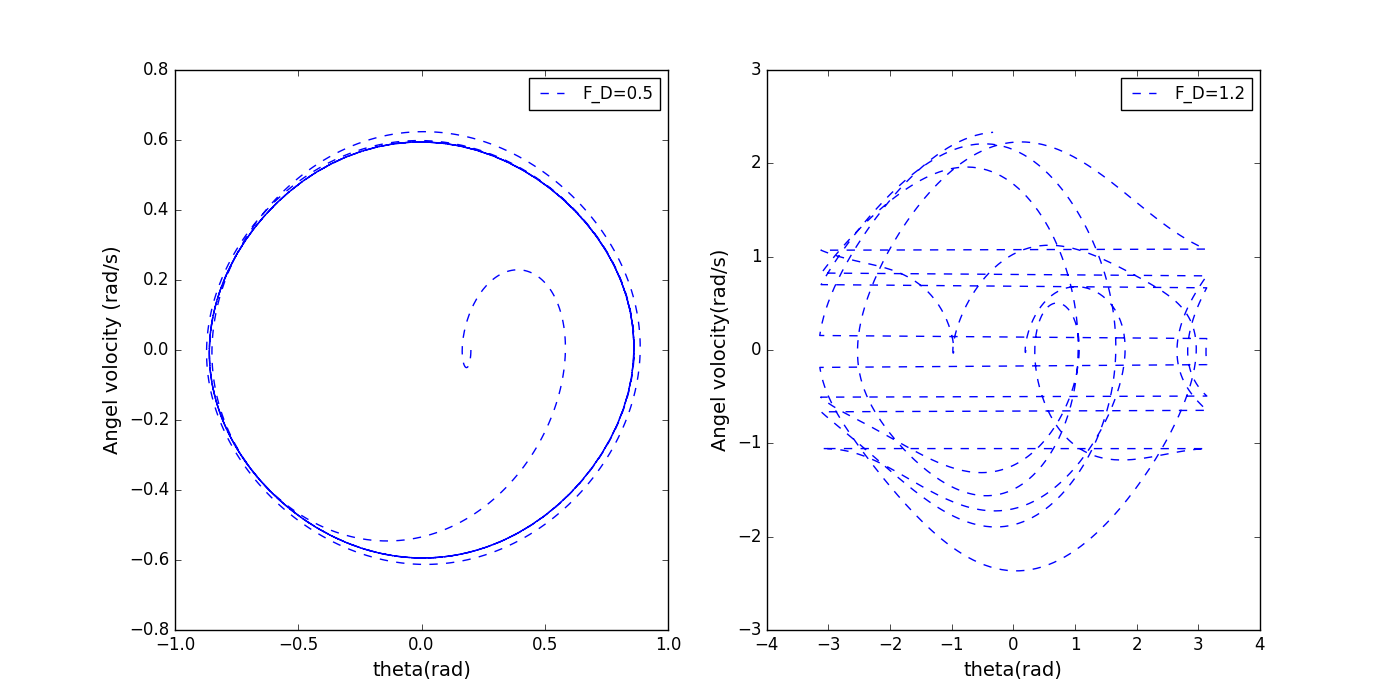
FIGURE 9.4

• 上图显示了在不同大小的驱动力力作用下，混沌摆在相空间中的运动图像，其中参数的取值为:$F_{D}=0.5,1.2;q=1/2,\Omega_{D}=2/3,dt=0.04;\theta(0)=0.2;\omega(0)=0$
  所有参数的单位均为国际单位。

下面分析在不同时间间隔下的Poincare Section：
计算程序为homework_9_3
截取特定时间的关键步骤：

dt=3.0*math.pi/1000  ＃驱动力角频率为2/3
#判断方法
if i%1000==0:  #对应第一种
if i%1000==500:  #对应第二种
if i%1000==125:  #对应第三种

除特别标出的以外，参数取值与前面相同

• 取样时刻设定为：$\Omega_{D}t=2n\pi$

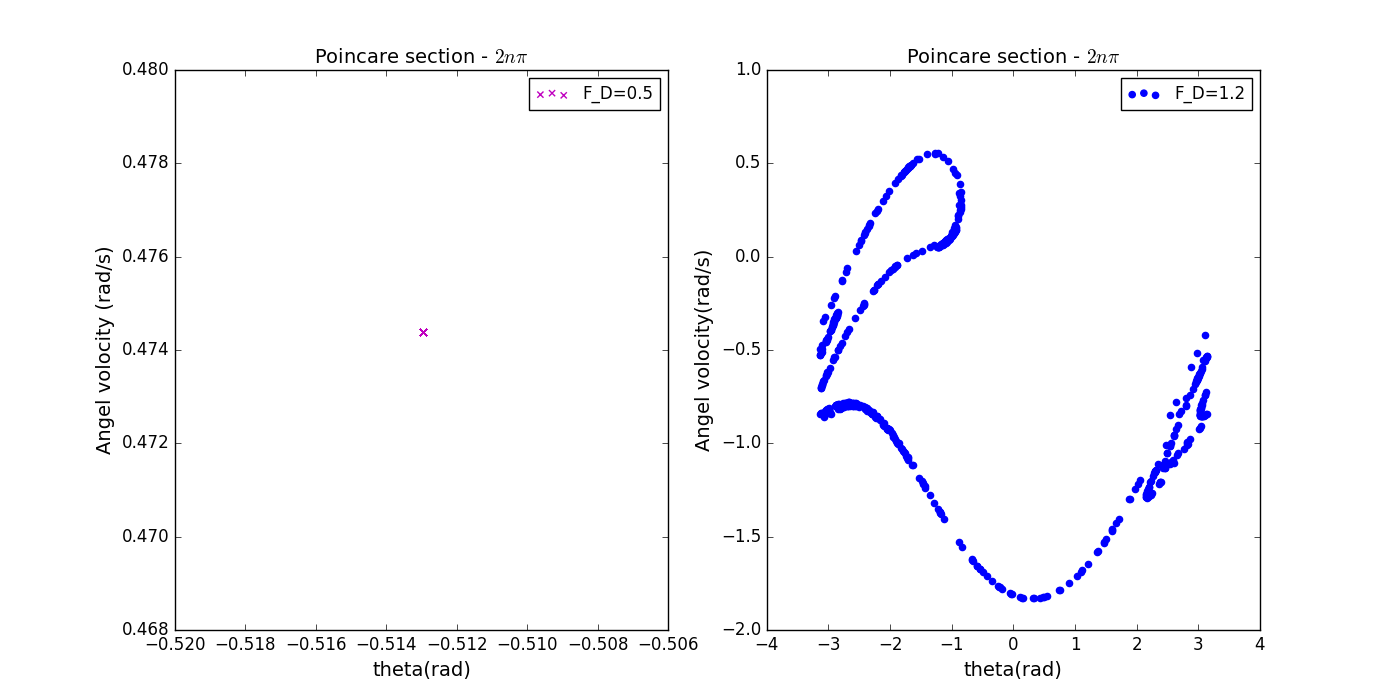
• 取样时刻设定为：$\Omega_{D}t=2n\pi+\pi$

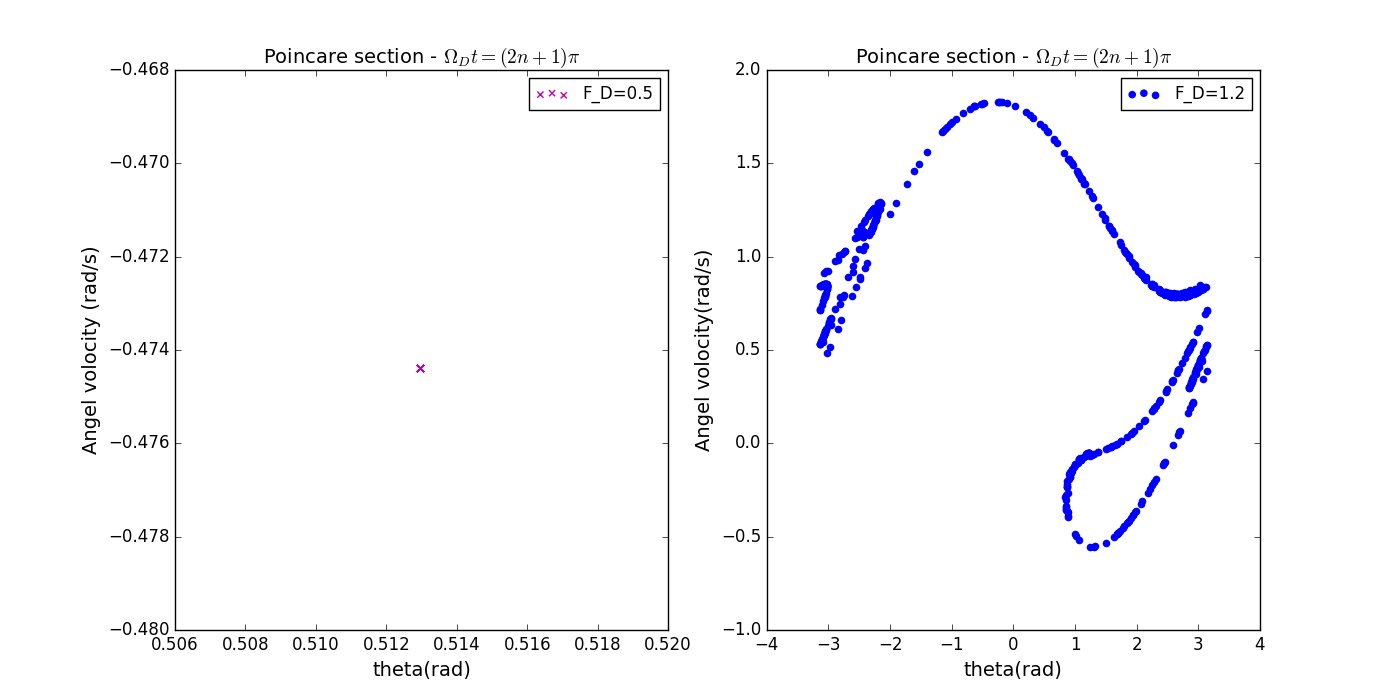
• 取样时刻设定为：$\Omega_{D}t=2n\pi+\frac{\pi}{4}$

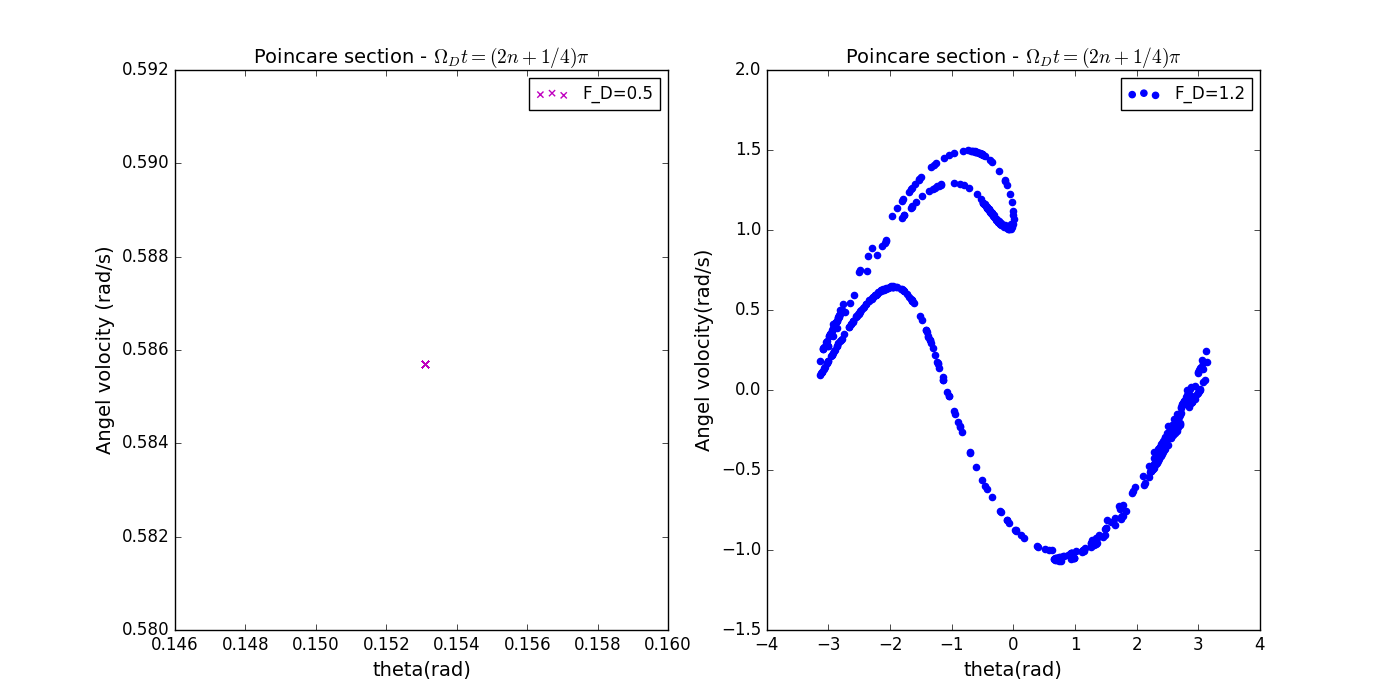
第一个图和第二个图正好可以将对方绕中心旋转180度得到，但是第三个图却没有类似性质。没有混沌时始终为一个点。

初始条件的细小改变对strange attractor的影响

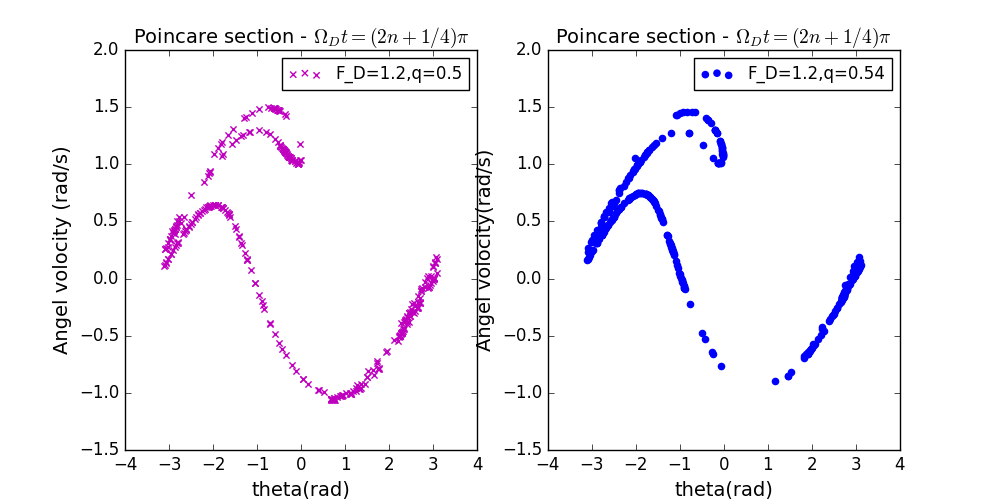
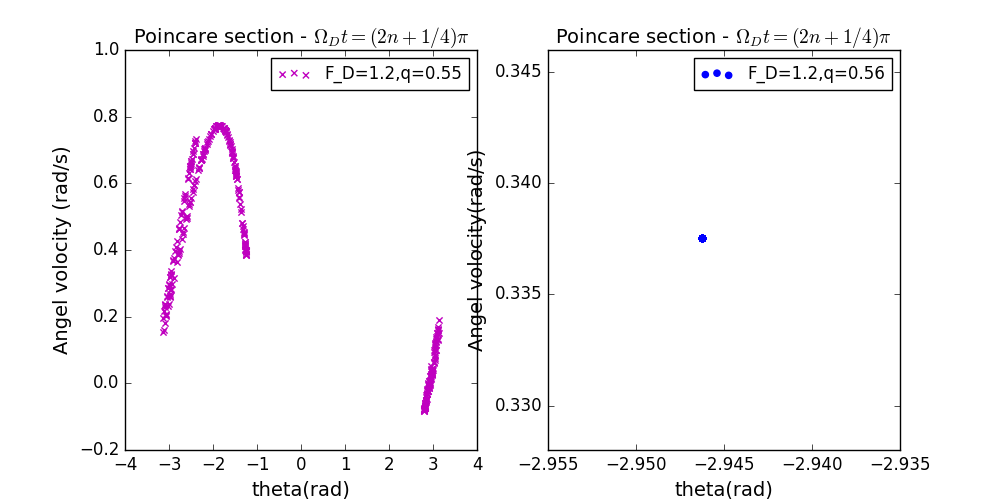
• 耗散力系数q的微小改变对strange attractor的影响

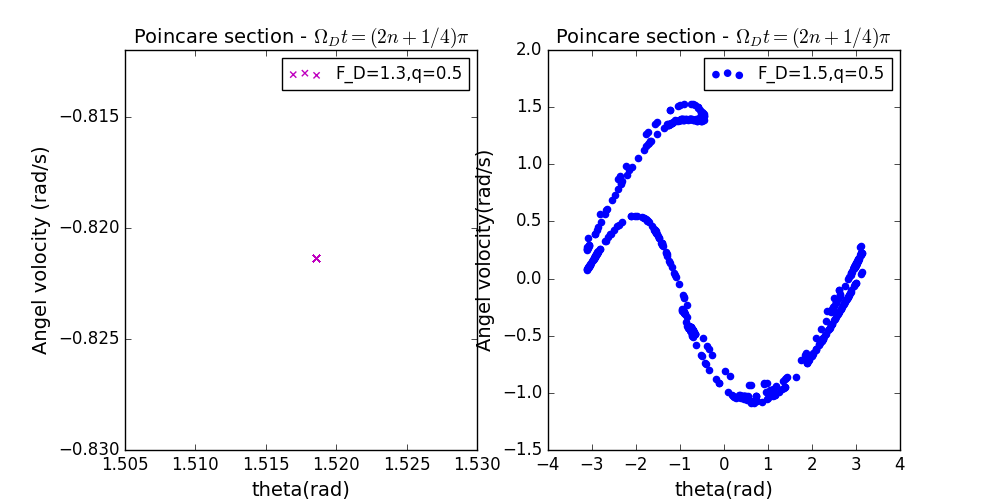
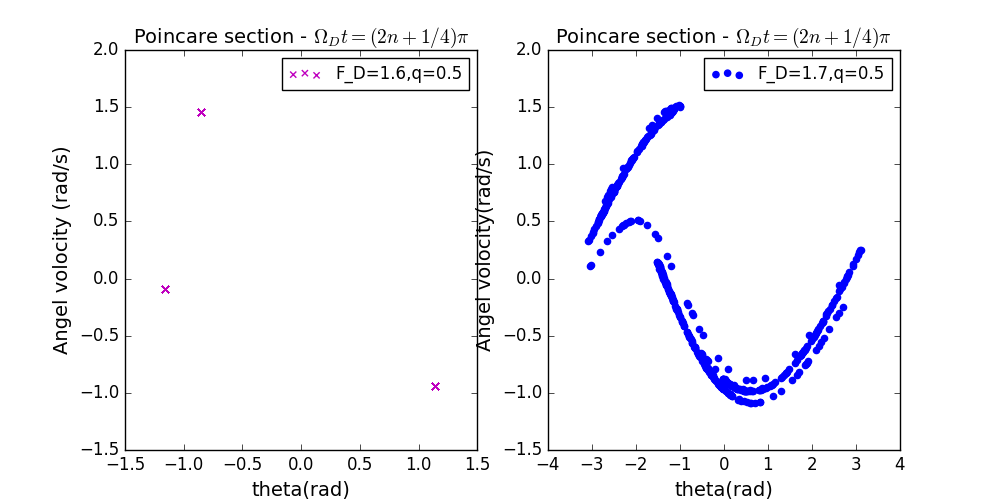
• 驱动力振幅$F_D$的微小改变对strange attractor的影响

• 驱动力角频率$\Omega_D$的微小改变对strange attractor的影响。(此时的观察时刻还是按照$\Omega_D=2/3$的情形选取)

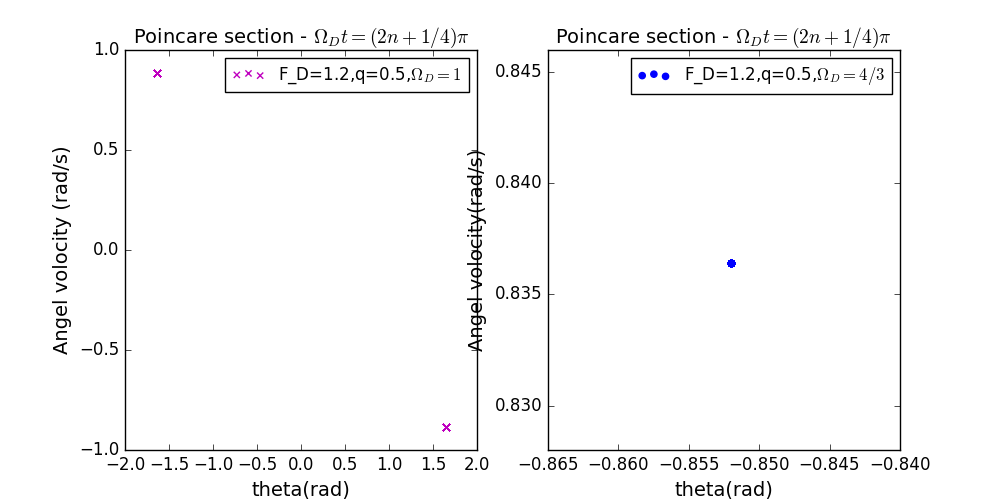
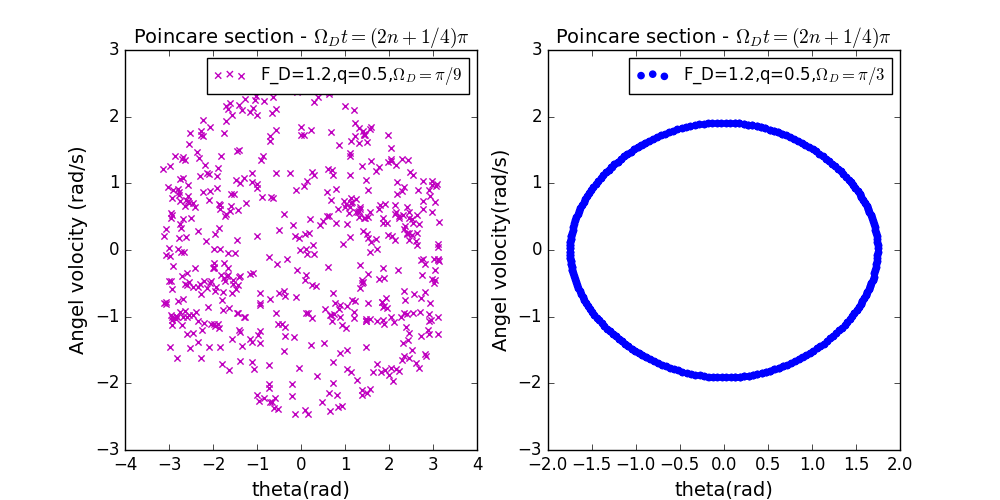
此时第四个图出现的原因是，运动没有出现混沌，由于采样周期相对其运动周期太短，导致图像和没有采样周期时相同。
改变驱动力频率三个图都没有出现strange attractor，说明采样周期和驱动力周期需要满足某种关系才能观察到strange attractor。

参考文献与致谢

• Computational Physics, Nicholas J. Giordano & Hisao Nakanishi

• How to think like a computer scientist -- Learning with Python: Interactive Edition 2.0

• Python图表绘制：matplotlib绘图库入门