@richey 2016-04-15T12:16:25.000000Z 字数 6556 阅读 1591

机器学习笔记1-回归问题

机器学习 回归 梯度下降

机器学习笔记1-回归问题
1 线性回归（Linear Regression）
2 逻辑回归
3 Softmax回归

1 线性回归（Linear Regression）

1.1 线性回归入门示例

先看个例子，比如，想用面积和卧室个数来预测房屋的价格
训练集如下：
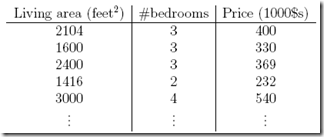
beIZFr.png-11.7kB
首先，我们假设为线性模型，那么hypotheses定义为

$h_\theta(\vec{x}) = \theta_0 + \theta_1x_1 + \theta_2x_2\tag{1.1}$
其中

$x_1,x_2$ 表示面积和#bedrooms（卧室）两个特征（feature）
那么对于线性模型，更为通用的写法为

$h(\vec{x}) = \sum_{i=0}^n\theta_ix_i = \vec{\theta}^{{T}}\cdot\vec{x} \tag{1.2}$
其中把

$\vec{\theta}$ 和

$\vec{x}$ 看成向量，并且

$x_0=1$ ，就可以表示成最后那种，两个向量相乘的形式。

$h_\theta(\vec{x}) = \vec{\theta} ^{T}\cdot\vec{x}\tag{1.3}$
线性回归的目的，就是通过训练集找出使得误差最小的一组参数

$\vec{\theta}$ （称为学习）,为了可以量化误差，定义代价函数（cost function）

$J(\vec{\theta}) = \frac{1}{2}\sum_{i=0}^m (h_\theta(\vec{x^{(i)}})-y^{(i)})^2 \tag{1.4}$
比较好理解，就是训练集中所有样本点，真实值和预测值之间的误差的平方和,其中1/2是为了后面计算方便，求导时会消掉,所以我们目的就是找到 $\vec{\theta}$ 使得 $J(\vec{\theta})$ 最小，这就是最小二乘法（最小平方），很容易理解。
richey批注：这里的m代表m个训练样本，每个样本有n个特征( $\theta$ 的纬度)。

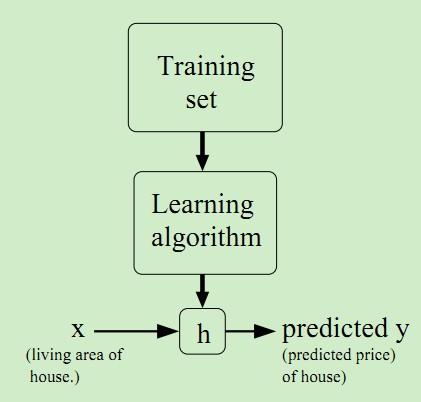
291925279255104.jpg-22kB

1.2 梯度下降法（gradient descent）

为了求解这个最优化问题，即找到 $\vec{\theta}$ 使得 $J(\vec{\theta})$ 最小，可以有很多方法。
先介绍梯度下降法 ,这是一种迭代方法，先随意选取初始 $\vec{\theta}$ ，比如 $\vec{\theta} =\vec{0}$ ，然后不断的以梯度的方向修正 $\vec{\theta}$ ，最终使 $J(\vec{\theta})$ 收敛到最小。
当然梯度下降找到的最优是局部最优，也就是说选取不同的初值，可能会找到不同的局部最优点，但是对于最小二乘的代价函数模型，比较简单只有一个最优点，所以局部最优即全局最优。
对于某个参数的梯度，其实就是 $J(\vec{\theta})$ 对该参数求导的结果，所以对于某个参数每次调整的公式如下:

$\theta_j := \theta_j -\alpha\frac{\partial}{\partial\theta_j}(J(\theta)) \tag{1.5}$
此处:=为赋值运算

$\alpha$ 称为“学习率”（learning rate），代表下降幅度，步长，小会导致收敛慢，大会导致错过最优点，所以公式含义就是，每次在梯度方向下降一步。
下面继续推导，假设训练集里面只有一个样本点，那么梯度推导为:

$\frac{\partial}{\partial\theta_j}(J(\vec{\theta})) = \frac{\partial}{\partial\theta_j}(\frac{1}{2}(h_\theta(\vec{x})-y)^2)$

$= 2\cdot\frac{1}{2}(h_\theta(x)-y) \cdot \frac{\partial}{\partial\theta_j}(h_\theta(x)-y)$

$= (h_\theta(x)-y) \cdot \frac{\partial}{\partial\theta_j}(\sum_{i=0}^n\theta_ix_i - y)$

$= (h_\theta(x)-y) \cdot x_j \tag{1.6}$

richey注解： $i$ 取 $1,2,3...,n$ ， $n$ 是特征的纬度，注意到上式是对 $\theta_j$ 求偏导，因此第3个式子中只有 $\frac{\partial (\theta_j x_j)}{\partial\theta_j} = x_j \not=0$ ,其他项对 $\theta_j$ 的偏导数为零。

1.2.1 批梯度下降法

就是求导过程，但是实际训练集中会有m个样本点,所以最终递推公式为：
重复迭代以下直至收敛｛

对 每 个

$\theta_j := \theta_j + \alpha \sum _{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} ({对每个j}\tag{1.7})$
｝
因为

$\vec{\theta}$ 中有多个参数，所以每次迭代对于每个参数都需要进行梯度下降，直到

$J(\vec{\theta})$ 收敛到最小值,这个方法称为批梯度下降（batch gradient descent），理由是每次计算梯度都需要遍历所有的样本点，这是因为梯度

$\nabla$ 是

$J(\vec{\theta})$ 的导数，而

$J(\vec{\theta})$ 是需要考虑所有样本的误差和。
批梯度下降方法的问题就是当样本点很大的时候，基本就没法算了（每次迭代都遍历样本空间一遍）。

1.2.2 随机梯度下降法

所以提出一种stochastic gradient descent（随机梯度下降），想法很简单，即每次只考虑一个样本点，而不是所有样本点，那么公式就变为：

Loop{
for i in m,{

对 每 个

$\theta_j := \theta_j + \alpha (y^{(i)} - h_\theta(x) )x_j^{(i)} (对每个j) \tag{1.8}$
{
}
其实意思就是，每次迭代只是考虑让该样本点的

$J(\vec{\theta})$ 趋向最小，而不管其他的样本点,这样算法会很快，但是收敛的过程会比较曲折，适合用于较大训练集的场景。
梯度下降法的缺点：

需要预先选定Learning rate；
需要多次iteration；
需要Feature Scaling；

1.3 最小二乘法（LMS）

其推导过程的思路：
推导得出 $J(\vec{\theta})$ 的矩阵表达式，梯度为零时的 $J(\vec{\theta})$ 取得最小值。

$\vec{\theta} = (X^TX)^{-1} X^{T} \vec{y} \tag{1.9}$
相当于通过求解矩阵方程得到

$\mathrm{min}(J(\vec{\theta}))$ 的解析解。

1.4 加权线性回归

首先考虑下图中的几种曲线拟合情况：
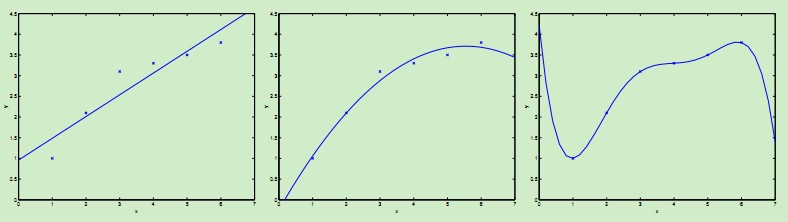
302140093624493.jpg-24.1kB
最左边的图使用线性拟合，但是可以看到数据点并不完全在一条直线上，因而拟合的效果并不好。如果我们加入 $x^2$ 项，得到，如中间图所示，该二次曲线可以更好的拟合数据点。
我们继续加入更高次项，可以得到最右边图所示的拟合曲线，可以完美地拟合数据点，最右边的图中曲线为5阶多项式，可是我们都很清醒地知道这个曲线过于完美了，对于新来的数据可能预测效果并不会那么好。
对于最左边的曲线，我们称之为欠拟合--过小的特征集合使得模型过于简单不能很好地表达数据的结构，最右边的曲线我们称之为过拟合--过大的特征集合使得模型过于复杂。
　　正如上述例子表明，在学习过程中，特征的选择对于最终学习到的模型的性能有很大影响，于是选择用哪个特征，每个特征的重要性如何就产生了加权的线性回归。在传统的线性回归中，学习过程如下：

Fit $\vec{\theta}$ to minimaize $\sum _i ^m (y^{(i)}-\vec{\theta}^T \vec{x^{(i)}})^2$
Output: $\vec{\theta}^T \vec{x}$

richey注解：以上求和 $\sum$ 将m个样本同等看待

而加权线性回归学习过程如下：
1. Fit $\vec{\theta}$ to minimaize $\sum _i ^n w^{(i)}(y^{(i)}-\vec{\theta}^T \vec{x^{(i)}})^2$
2. Output: $\vec{\theta}^T \vec{x}$
　　二者的区别就在于对不同的样本赋予了不同的非负值权重 $w^{(i)}$ ，权重越大，对于代价函数的影响越大。一般选取的权重计算公式为：

$w^{(i)} = \mathrm{exp}(-\frac{(x^{(i)}-x)^2}{2\tau^2}) \tag{1.10}$ 其中，x是要预测的特征，表示离x越近的样本权重越大，越远的影响越小。
总结一下：加权线性回归LWR算法是一种non-parametric（非参数）学习算法，而线性回归则是一种parametric（参数）学习算法。
所谓参数学习算法它有固定的明确的参数，参数一旦确定，就不会改变了，我们不需要在保留训练集中的训练样本。
而非参数学习算法，每进行一次预测，就需要重新学习一组，是变化的，所以需要一直保留训练样本。也就是说，当训练集的容量较大时，非参数学习算法需要占用更多的存储空间，计算速度也较慢。有得必有失，效果好当然要牺牲一些其他的东西。

1.5 代码实现

1.5.1 使用scikit-learn库

1.5.1.1 最小二乘法

1.5.2 不使用库

from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(filename):
    numFeat = len(open(filename).readline().split('\t'))-1
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip('\n').split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat
def standMaReg(xArr, yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    xTx  = xMat.T*xMat
    if linalg.det(xTx)==0.0:
        print 'This matrix is singular, connot do inverse'
        return
    ws = xTx.I*(xMat.T*yMat)
    return ws
def standBaGradReg(xArr, yArr, alpha=0.001, iter_num=15):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m,n=shape(xMat)
    weights = mat(ones((n,1)))
    for i in range(iter_num):
        yPredict = mat(xMat*weights)
        tmp=mat(zeros((n,1)))
        for j in range(n):
            tmp[j,:] += alpha*sum(multiply((yMat-yPredict),xMat[:,j]))
        weights = weights + tmp
    return weights
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))
    for j in range(m):
        diffMat = testPoint - xMat[j,:]
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T*(weights*xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I*(xMat.T*(weights*yMat))
    return testPoint*ws
def lwlrTest(testArr, xArr, yArr, k=1.0):
    m = shape(testArr)[0]
    yPre = zeros(m)
    for i in range(m):
        yPre[i] = lwlr(testArr[i], xArr, yArr, k)
    return yPre
def ridgeRegres(xMat, yMat, lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[1])*lam
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
    ws = denom.I*(xMat.T*yMat)
    return ws
def ridgeTest(xArr, yArr, numIter=30):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean
    xMeans = mean(xMat, 0)
    xVar = var(xMat, 0)
    xMat = (xMat - xMeans)/xVar
    wMat = zeros((numIter,shape(xMat)[1]))
    lamList = []
    for i in range(numIter):
        lamList.append(exp(i-10))
        ws = ridgeRegres(xMat, yMat, exp(i-10))
        wMat[i,:]=ws.T
    return wMat, lamList
def plotReg(weights, xArr, yArr, xIndex=0):
    xMat = mat(xArr)
    yMat = mat(yArr)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xMat[:,xIndex].flatten().A[0], yMat.T[:,0].flatten().A[0])
    yPredict = xMat*weights
    ax.plot(xMat[:,xIndex], yPredict)
    plt.show()
xArr, yArr = loadDataSet("ex0.txt")
ws1 = standMaReg(xArr, yArr)
print "ws1", ws1
plotReg(ws1, xArr, yArr, 1)
ws2 = standBaGradReg(xArr, yArr, 0.001, 1000)
print "ws2", ws2
yPre = lwlrTest(xArr, xArr, yArr, 0.01)
xMat = mat(xArr)
srtInde = xMat[:,1].argsort(0)
xSort = xMat[srtInde][:,0,:]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1], yPre[srtInde])
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0], s=2, c='red')
plt.show()
abX, abY = loadDataSet('abalone.txt')
weights, lam = ridgeTest(abX, abY)
plt.plot(weights)
plt.show()

2 逻辑回归

3 Softmax回归

1 http://www.cnblogs.com/fxjwind/p/3626173.html?utm_source=tuicool&utm_medium=referral
2 http://blog.csdn.net/moodytong/article/details/10041547
3 http://www.cnblogs.com/fanyabo/p/4060498.html