Python分享

分享

Python是一门解释型的动态强类型语言。在1989年圣诞节期间，著名的“龟叔”Guido van为了打发无聊的圣诞节编写了Python，目前成为主要是用来编写应用程序的高级抽象语言。

在Python社区，吉多·范罗苏姆被人们认为是“仁慈的独裁者”（BDFL），意思是他仍然关注Python的开发进程，并在必要的时刻做出决定。

从彩蛋看Python的设计理念

import this
from __future__ import braces  # 引入大括号
import antigravity  # 反重力对话

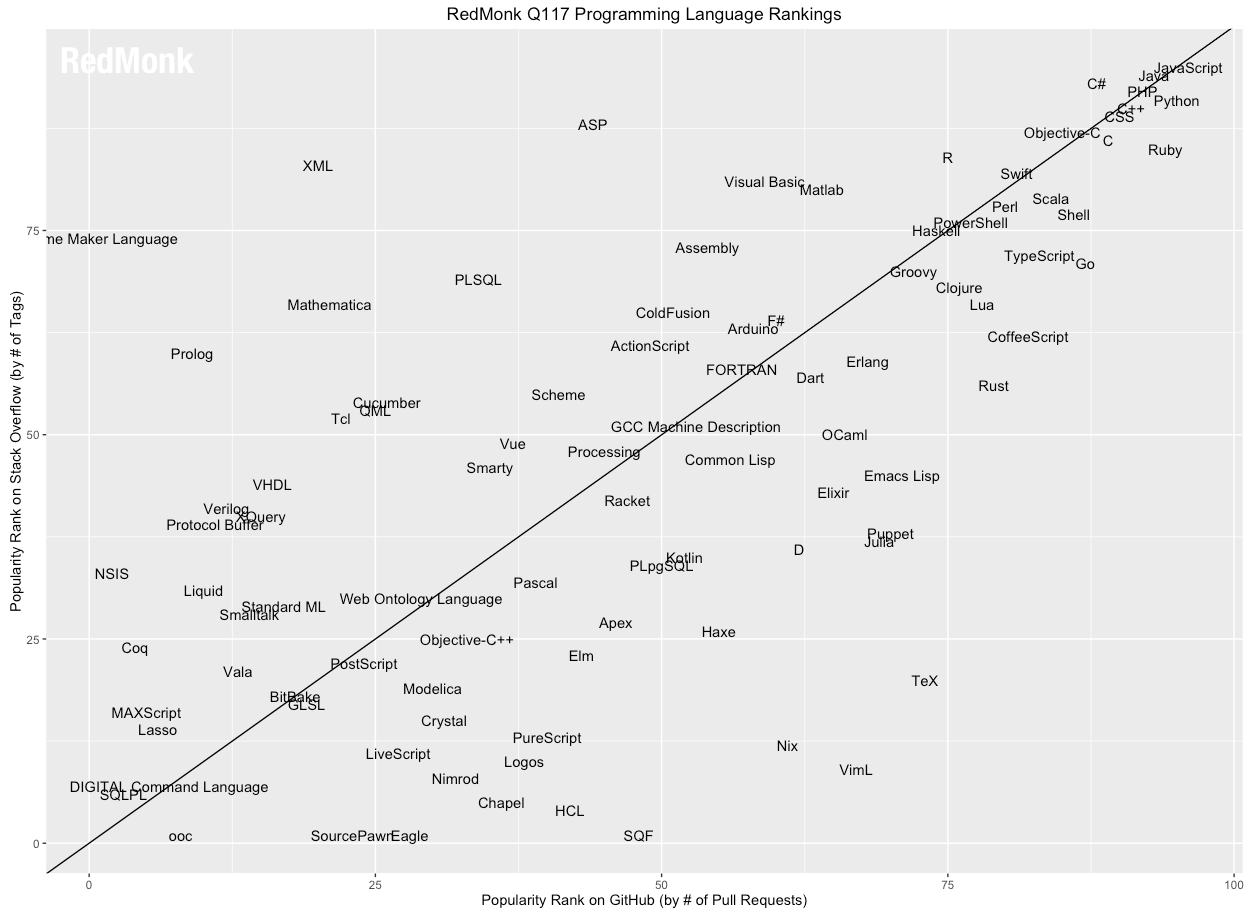
redmonk2017年6月受欢迎语言排行榜

1 JavaScript
2 Java
3 Python
4 PHP
5 C#
5 C++
7 CSS
7 Ruby
9 C
10 Objective-C
11 Scala
11 Shell
11 Swift
14 R
15 Go
15 Perl
17 TypeScript
18 PowerShell
19 Haskell
20 Clojure
20 CoffeeScript
20 Lua
20 Matlab

Python的优缺点

Python的优缺点

使用感受
1. 高度封装：代码行数少，可读性强。
2. 库丰富：不需要重复造轮子。
3. 优势多：科学运算、数据处理是标杆，网站、后台服务、日常工具，系统管理员脚本、自动化测试等方面都是优势语言。
4. 处理速度慢：老生常谈
5. 编码问题是大坑
6. 不能加密（误）

作为当前三驾马车之一，Python注重解放程序员的生产力，让程序员注重解决问题而不是程序实现，加上语言本身简单易学，应用范围广，注重传播，让Python受欢迎程度大大提高。另一方面，Python委员会的保守让很多人对Python的长远发展持悲观态度。

python、JAVA在解八皇后问题的代码对比

八皇后问题是一个以国际象棋为背景的问题：如何能够在 8×8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。

Python

def conflict(state,nextX):
    nextY=len(state)
    for i in range(nextY):
        if abs(state[i]-nextX)in(0,nextY-i):
            return True
    return False
def queens(num=8,state=()):
    for pos in range(num):
        if not conflict(state,pos):
            if len(state)==num-1:
                yield(pos,)
            else:
                for result in queens(num,state+(pos,)):
                    yield (pos,)+result
def prettyprint(solution):
    def line(pos,length=len(solution)):
        return '. '*(pos)+'X '+'. '*(length-pos-1)
    for pos in solution:
        print(line(pos))
for i in range(92):
    prettyprint(list(queens(8))[i])
    print('_'*16)

JAVA

public class Queen {  
    //定义两个int型变量，用于以下循环程序。  
    private int i,k;  
    //列指示器  
    private int pointer = 1;  
    //解  
    int[] cellpos = new int[9];  
    public Queen() {  
        cellpos[pointer] = 1;  
        cellpos[2] = 3;  
        pointer = 3;  
        //给第二列之后的列赋一个初值1,因为默认是0,而我们约定的是从1开始.  
        clean(2);  
        while(cellpos[1] <= 8) {  
            /** 
             * 特殊点第一列,这里不写cellpos[pointer]++; 
             * 是因为后面的程序中已经加过了. 
             * 这点不是特殊点，更新时间（2010-3-15 22:06） 
             */  
            //if(pointer == 1) {  
                //cellpos[pointer]++;  
                //pointer++;  
                //continue;  
            //}  
            /** 
             * 特殊点第八行,这里为什么还要加一个判断呢 
             * 也许你会问后面不是有i>8判断吗?试想一下,当倒数第二列 
             * 正好等于8,求完解后,回到倒数第二列, 
             * 并且后面的程序会使倒数第二列加1,现在还认为它多余么. 
             */  
            if(cellpos[pointer]>8) {  
                pointer--;  
                cellpos[pointer]++;  
                //清理  
                clean(pointer);  
                continue;  
            }  
            /** 
             * 扫描 
             */  
            for(i=cellpos[pointer]; i<=8; i++)  
                if(canStay(i)) break;  
            if(i>8) {  
                pointer--;  
                cellpos[pointer]++;  
                //清理  
                clean(pointer);  
                continue;  
            }else{  
                cellpos[pointer] = i;  
            }  
            if(pointer==8) {  
                //将解打印出来  
                printQueen();  
                pointer--;  
                cellpos[pointer]++;  
                //清理  
                clean(pointer);  
            }else{  
                pointer++;  
            }  
        }  
    }  
    private boolean canStay(int ci) {  
        //行扫描,判断同一行是否有其它皇后.  
        for(k=1; k<pointer; k++)  
            if(cellpos[k]==ci) return false;  
        //对角线扫描,判断对角线上是否有其它皇后.注意有两条对角线.  
        for(k=1; k<pointer; k++)  
            if((ci==cellpos[k]+(pointer-k)) ||   
                (ci==cellpos[k]-(pointer-k)))  
                    return false;  
        return true;  
    }  
    private void clean(int pointer) {  
        for(k=pointer+1; k<9; k++)  
            cellpos[k] = 1;  
    }  
    private void printQueen() {  
        for(k = 1; k<9; k++) {  
            System.out.print(""+cellpos[k]);  
            if(k!=8)  
                System.out.print(",");  
        }  
        System.out.println();  
    }  
    public static void main(String[] args) {  
        new Queen();  
    }  
}  

Python在当前的应用

产品：
youtube，豆瓣，知乎

领域：
数据分析/处理平台：比如机器学习、深度学习、量化金融。
web框架：著名的Flask、tonardo、 django
大型爬虫项目：访问、解析和分布式优势很大。
各种脚本：运维、外挂、小工具...

“万物皆对象”

究竟何谓对象？不同的编程语言以不同的方式定义“对象”某些语言中，它意味着所有对象必须有属性和方法；另一些语言中，它意味着所有的对象都可以子类化。在 Python 中，定义是松散的；某些对象既没有属性也没有方法，而且不是所有的对象都可以子类化 。但是万物皆对象从感性上可以解释为：一切都可以赋值给变量或作为参数传递给函数。

在 Python 中万物皆对象。字符串是对象。列表是对象。函数是对象，甚至模块也是对象。
演示：字符串乘法、列表乘法、元组乘法

高级特性

迭代器

迭代器是访问集合元素的一种方式。迭代器对象从集合的第一个元素开始访问，直到所有的元素被访问完结束。迭代器只能往前不会后退，并且使用后销毁。

迭代器的一大优点是不要求事先准备好整个迭代过程中所有的元素。迭代器仅仅在迭代到某个元素时才计算该元素，而在这之前或之后，元素可以不存在或者被销毁。这个特点使得它特别适合用于遍历一些巨大的或是无限的集合，比如几个G的文件，或是斐波那契数列等等。

ita = iter([1, 2, 3])
type(ita)
# list_iterator
next(ita)
# 1
next(ita)
# 2
next(ita)
# 3
next(ita)
# StopIteration
# Traceback (most recent call last)
# <ipython-input-169-263544bbe47a> in <module>()
# ----> 1 next(ita)
# StopIteration: 

生成器

在计算中，受到内存限制，列表容量肯定是有限的。如果创建一个包含100万个元素的列表，不仅占用很大的存储空间，如果我们仅仅需要访问前面几个元素，那后面绝大多数元素占用的空间都白白浪费了。

所以，如果列表元素可以按照某种算法推算出来，那我们是否可以在循环的过程中不断推算出后续的元素呢？这样就不必创建完整的list，从而节省大量的空间。在Python中，这种一边循环一边计算的机制，称为生成器（Generator）

生成器每次运行到yield被挂起，同时保存状态；下一次调用，会从生成器被冻结的状态继续运行。依赖于惰性计算，生成器只有在请求到来时才会计算下次数据内容。

def fib():
    x, y = 0, 1
    while True:
        yield x
        x, y = y, x + y
from itertools import *
# 用 itertools.islice 方法获得级数的前 n 项
list(islice(fib(), 10))
# [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
# 用takewhile得到所有1000以下的斐波那契数
list(takewhile(lambda x: x < 1000, fib()))
# [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987]
# 第二十项
next(islice(fib(), 20, None))
# 6765
# 第一个大于100000的项
next(filter(lambda x: x > 100000, fib()))
# 121393

装饰器

装饰器本质上是一个Python函数，它可以让其他函数在不需要做任何代码变动的前提下增加额外功能。它经常用于有切面需求的场景，比如：插入日志、性能测试、事务处理、缓存等场景。有了装饰器，我们就可以抽离出大量与函数功能本身无关的雷同代码并继续重用。

打个比方，平时我们穿内裤遮羞，但是到了冬天没法帮我们防风御寒，于是我们发明了长裤（装饰器），在不脱内裤的情况下完成所有的需求。
简单示例

def foo(func):  
    print 'decorator foo'  
    return func  
@foo  
def bar():  
    print 'bar'  
bar()  

假设目前需要实现一个性能分析器，并接收一个参数，来控制性能分析器是否生效，其模拟代码如下

import time  
def function_performance_statistics(trace_this=True):  
    if trace_this:  
       def performace_statistics_delegate(func):  
            def counter(*args, **kwargs):  
                start = time.clock()  
                func(*args, **kwargs)  
                end =time.clock()  
                print 'used time: %d' % (end - start, )  
            return counter  
    else:  
       def performace_statistics_delegate(func):  
            return func  
    return performace_statistics_delegate  
@function_performance_statistics(True)  
def add(x, y):  
    time.sleep(3)  
    print 'add result: %d' % (x + y,)  
@function_performance_statistics(False)  
def mul(x, y=1):  
    print 'mul result: %d' % (x * y,)  
add(1, 1)  
mul(10)  

输出结果为：

add result: 2  
used time: 0  
mul result: 10  

一些方便的特性

1.1 拆箱

>>> a, b, c = 1, 2, 3
>>> a, b, c
(1, 2, 3)
>>> a, b, c = [1, 2, 3]
>>> a, b, c
(1, 2, 3)
>>> a, b, c = (2 * i + 1 for i in range(3))
>>> a, b, c
(1, 3, 5)
>>> a, (b, c), d = [1, (2, 3), 4]
>>> a
1
>>> b
2
>>> c
3
>>> d
4

1.2 拆箱变量交换

>>> a, b = 1, 2
>>> a, b = b, a
>>> a, b
(2, 1)

1.3 扩展拆箱

>>> a, *b, c = [1, 2, 3, 4, 5]
>>> a
1
>>> b
[2, 3, 4]
>>> c
5

1.4 负数索引

>>> a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a[-1]
10
>>> a[-3]
8

1.5 切割列表

>>> a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a[2:8]
[2, 3, 4, 5, 6, 7]

1.6 负数索引切割列表

>>> a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a[-4:-2]
[7, 8]

1.7指定步长切割列表

>>> a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a[::2]
[0, 2, 4, 6, 8, 10]
>>> a[::3]
[0, 3, 6, 9]
>>> a[2:8:2]
[2, 4, 6]

1.8 负数步长切割列表

>>> a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a[::-1]
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
>>> a[::-2]
[10, 8, 6, 4, 2, 0]

1.9 列表切割赋值

>>> a = [1, 2, 3, 4, 5]
>>> a[2:3] = [0, 0]
>>> a
[1, 2, 0, 0, 4, 5]
>>> a[1:1] = [8, 9]
>>> a
[1, 8, 9, 2, 0, 0, 4, 5]
>>> a[1:-1] = []
>>> a
[1, 5]

1.10 命名列表切割方式

>>> a = [0, 1, 2, 3, 4, 5]
>>> LASTTHREE = slice(-3, None)
>>> LASTTHREE
slice(-3, None, None)
>>> a[LASTTHREE]
[3, 4, 5]

1.11 列表以及迭代器的压缩和解压缩

>>> a = [1, 2, 3]
>>> b = ['a', 'b', 'c']
>>> z = zip(a, b)
>>> z
[(1, 'a'), (2, 'b'), (3, 'c')]
>>> zip(*z)
[(1, 2, 3), ('a', 'b', 'c')]

1.12 列表相邻元素压缩器

>>> a = [1, 2, 3, 4, 5, 6]
>>> zip(*([iter(a)] * 2))
[(1, 2), (3, 4), (5, 6)]
>>> group_adjacent = lambda a, k: zip(*([iter(a)] * k))
>>> group_adjacent(a, 3)
[(1, 2, 3), (4, 5, 6)]
>>> group_adjacent(a, 2)
[(1, 2), (3, 4), (5, 6)]
>>> group_adjacent(a, 1)
[(1,), (2,), (3,), (4,), (5,), (6,)]
>>> zip(a[::2], a[1::2])
[(1, 2), (3, 4), (5, 6)]
>>> zip(a[::3], a[1::3], a[2::3])
[(1, 2, 3), (4, 5, 6)]
>>> group_adjacent = lambda a, k: zip(*(a[i::k] for i in range(k)))
>>> group_adjacent(a, 3)
[(1, 2, 3), (4, 5, 6)]
>>> group_adjacent(a, 2)
[(1, 2), (3, 4), (5, 6)]
>>> group_adjacent(a, 1)
[(1,), (2,), (3,), (4,), (5,), (6,)]

1.13 在列表中用压缩器和迭代器滑动取值窗口

>>> def n_grams(a, n):
... z = [iter(a[i:]) for i in range(n)]
... return zip(*z)
...
>>> a = [1, 2, 3, 4, 5, 6]
>>> n_grams(a, 3)
[(1, 2, 3), (2, 3, 4), (3, 4, 5), (4, 5, 6)]
>>> n_grams(a, 2)
[(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)]
>>> n_grams(a, 4)
[(1, 2, 3, 4), (2, 3, 4, 5), (3, 4, 5, 6)]

1.14 用压缩器反转字典

>>> m = {'a': 1, 'b': 2, 'c': 3, 'd': 4}
>>> m.items()
[('a', 1), ('c', 3), ('b', 2), ('d', 4)]
>>> zip(m.values(), m.keys())
[(1, 'a'), (3, 'c'), (2, 'b'), (4, 'd')]
>>> mi = dict(zip(m.values(), m.keys()))
>>> mi
{1: 'a', 2: 'b', 3: 'c', 4: 'd'}

1.15 列表展开

>>> a = [[1, 2], [3, 4], [5, 6]]
>>> list(itertools.chain.from_iterable(a))
[1, 2, 3, 4, 5, 6]
>>> sum(a, [])
[1, 2, 3, 4, 5, 6]
>>> [x for l in a for x in l]
[1, 2, 3, 4, 5, 6]
>>> a = [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]
>>> [x for l1 in a for l2 in l1 for x in l2]
[1, 2, 3, 4, 5, 6, 7, 8]
>>> a = [1, 2, [3, 4], [[5, 6], [7, 8]]]
>>> flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x]
>>> flatten(a)
[1, 2, 3, 4, 5, 6, 7, 8]

延伸

Python之禅的翻译和理解

优美胜于丑陋（Python以编写优美的代码为目标）
明了胜于晦涩（优美的代码应当是明了的，命名规范，风格相似）
简洁胜于复杂（优美的代码应当是简洁的，不要有复杂的内部实现）
复杂胜于凌乱（如果复杂不可避免，那代码间也不能有难懂的关系，要保持接口简洁）
扁平胜于嵌套（优美的代码应当是扁平的，不能有太多的嵌套）
间隔胜于紧凑（优美的代码有适当的间隔，不要奢望一行代码解决问题）
可读性很重要（优美的代码是可读的）
即便假借特例的实用性之名，也不可违背这些规则（这些规则至高无上）
不要包容所有错误，除非你确定需要这样做（精准地捕获异常，不写 except:pass 风格的代码）
当存在多种可能，不要尝试去猜测
而是尽量找一种，最好是唯一一种明显的解决方案（如果不确定，就用穷举法）
虽然这并不容易，因为你不是 Python 之父（这里的 Dutch 是指 Guido ）
做也许好过不做，但不假思索就动手还不如不做（动手之前要细思量）
如果你无法向人描述你的方案，那肯定不是一个好方案；反之亦然（方案测评标准）
命名空间是一种绝妙的理念，我们应当多加利用（倡导与号召）

弱类型、强类型、动态类型、静态类型语言的区别

弱类型、强类型、动态类型、静态类型语言的区别是什么？

Python代码混淆

python 代码加密甚至可以做到比用汇编手写混淆，用 c 手写混淆更加难以解密。具体做法略复杂仅简单说个过程。

第一级别是源码级别的混淆，用 ast 和 astor ，再自己手写一个混淆器，三五百行的脚本直接混淆到几万行，整个文件面目全非，基本可以做到就算直接放脚本给你拿去逆，除非你再写出来一个逆向前面的混淆算法的脚本来逆（在熟悉 python 的情况下需要花几天，且不说需要了解程序构造原理），手动去调试脚本几乎达到不可行的地步（话费时间再乘以 2 ）

第二级别是个性化定制 pyinstaller ， pyinstaller 会打包所有需要的库，将脚本也包含进打包的 exe ，但是， pyinstaller 有一个 stub ，相当于一个启动器，需要由这个启动器来解密脚本和导入模块，外面有直接导出脚本的工具，但是那是针对 pyinstaller 自带的启动器做的，完全可以自己修改这个启动器再编译，这样逆向者就必须手动调试找到 main 模块。配合第一级别加密，呵呵，中国就算是最顶尖的逆向专家也要花个一两周，来破解我们的程序逻辑了，就我所知，实际上国内对于 py 程序的逆向研究不多。

第三级别是再上一层，将 py 翻译为 c 再直接编译 c 为 dll ，配合第一阶段先混淆再转 c 再编译，在第一步混淆之后，会产生非常多垃圾（中间层）函数，这些中间层函数在 c 这里会和 py 解释器互相调用，脚本和二进制之间交叉运行，本身混淆之后的源码就极难复原，再混合这一层，想逆向，难。

第四级别是利用 py 的动态特性，绝大多数逆向者都是 c ，汇编出身，对于程序的第一直觉就是，程序就是一条一条的指令，后一条指令必然在这一条指令后面，然而， py 的动态特性可以让代码逻辑根本就不在程序里面，这一点不想多讲，涉及到我一个项目里的深度加密。

第五级别，数学做墙。了解过比特币原理的知道要想用挖比特币就得提供大量算力去帮网络计算 hash ，这个成为 pow ，那么既然已经采用 py 了估计已经不考虑太多 cpu 利用率了，那就可以采用 pow （还有其他的手段）确保程序运行时拥有大量算力，如果程序被单步调试，呵呵，一秒钟你也跑不出来几个 hash 直接拉黑这个 ip （这个说法可能比较难理解，因为我第四层的加密没有说明，不过意思就是拒绝执行就对了）