问题

深度学习

Q：逻辑回归的优缺点和使用场景。
A：场景：简单的分类概率场景。
优点：(1)计算复杂度低(2)鲁棒性好。
缺点：(1) 精度低容易欠拟合 (2)数据复杂时效果不佳。

Q：决策树优缺点和使用场景。
A：场景：各个分类和回归的场景，尤其是boost算法大行其道后，GBDT和GBDR等以决策树为基函数的模型在深度学习流行后依然有很亮眼的表现。
优点：(1)速度快(2)精度高(3)根据启发函数不同，可以支持离散和连续字段。
缺点: (1)需要剪枝，容易过拟合(2)特征相关性计算差，需要预先组合大量特征(3)需要样本均衡。

Q：神经网络拟合函数的原理是什么？
A：通用近似定理。根据通用近似定理，对于具有线性输出层和至少一个“挤压性质”（比如logistic、tanh）的激活函数组成的隐藏层神经网络，至少隐藏层神经元数量足够，可以以任意精度来近似任何一个在实数空间的有界闭集函数。

Q：卷积的本质是什么？
A：信息去噪，保留高频信号的同时降低噪音，类似于信息接近无损的转换。

Q：RELU优缺点？
A：优点：简单，计算快，效果好，导数大不容易梯度弥散。
缺点：在训练中变为0，无法继续迭代。解决方案：用leakey relu。

Q：图片增强为什么有效？
A：平移不变性特征，平移缩放旋转不影响语义信息，图像增强能在保持局部不变性时加大无关信息的噪音。

Q：感受野是什么？
A：单个神经元能收到的参数范围，一般来说，感受野越大，神经元越不容易过拟合，效果也更好。

Q：说明对于不同特征该如何进行特征工程？
A：对于数值特征，需要进行归一化处理，方便优化算法更快更好的找到最优解;对于类别特征，编码至对应框架可读的格式;对于学习能力不够强的模型，可以预先组合特征，只由模型计算贡献度分配问题，相当于先验知识;对特定的方向，以cv为例，图像增强是常见的特征处理方式，但仍需要注意业务场景，比如对人的识别不应该使用90度旋转增强。

Q：模型评估中的不同指标用在什么场景中？
A：分类模型中，可以考虑选择准确率指标;在测试集固定时，选择pr曲线;测试集不固定时或业务正确目标较难定义时，选择roc曲线。

Q：逻辑回归的应用场景、优势和区别。
A：场景：简单的分类概率场景。
优点：(1)计算复杂度低(2)鲁棒性好。
缺点：(1) 精度低容易欠拟合 (2)数据复杂时效果不佳。

Q：决策树的应用场景、优势和区别。
A：场景：各个分类和回归的场景，尤其是boost算法大行其道后，GBDT和GBDR等以决策树为基函数的模型在深度学习流行后依然有很亮眼的表现。
优点：(1)速度快(2)精度高(3)根据启发函数不同，可以支持离散和连续字段。
缺点: (1)需要剪枝，容易过拟合(2)特征相关性计算差，需要预先组合大量特征(3)需要样本均衡。

Q：简述深度学习中的优化方法，分为哪些形式？都有哪些问题？
A：深度学习使用主要使用梯度下降法来寻找一组最小结构风险的参数。梯度下降法可以分为批量梯度下降，随机梯度下降，小批量梯度下降三种形式。
除了收敛效果和效率上的差异，都存在共同的问题：1.如何初始化参数；2.预处理数据；3.选择h合适的学习率。
常见的改进方法从学习率衰减和梯度方向优化等两个方向进行改进。

Q：简述学习率衰减的优化方法。
A：常见的衰减算法主要按迭代次数衰减包括逆时衰减、指数衰减、自然指数衰减。
自动衰减方法有AdaGrad，RMSprop。
AdaGrad：在每次迭代中自适应调整每个参数的学习率，先对所有元素乘积计算每个参数梯度平方累计值，再计算算法的更新差值。对当次梯度进行计算并更新值。如果某个参数的偏导数累计比较大，其学习率相对较小；反之偏导越小，学习率相对较大。但整体是逐步缩小的。缺点是在经过一定次数迭代还未找到最优点时，梯度会接近小时，无法再继续前进。
RMSprop：带动量的AdaGrad，计算每次迭代的梯度平方的指数衰减移动平均 ，由于常常动量更大，在初始下降往往更快，也有更多的动量空间在一定次数迭代后也能继续寻找最优解。

Q：简述初始化方法。
A：gaussian初始化：最简单的初始化方法，参数从一个固定均值和固定方差的gaussion分布进行随机初始化。
Xavier初始化：一种按照均匀分布来初始化的参数，超参数可以根据神经元的链接数量或损失函数进行对应的调整，对logistics来说，为

Q：简述归一化方法
A：数据预处理：
缩放归一化：特征减去最小值，除以最大值减去最小值。将每个特征的取值范围归一到[-1, 1]之间。
标准归一化: 特征减去均值，除以标准差。将每一维特征都处理为标准正态分布。
白化：用主成分分析来降低特征之间的相关性。使所有特征具有相同的方差。
训练中归一化：
批量归一化（BN）：

Q：简述常见Normalization算法

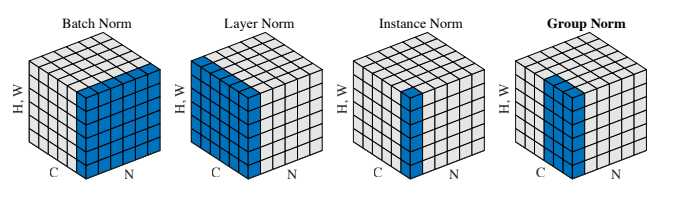
Batch Normalization（BN）：是最早出现也是效果最好的Normalization算法。
对其求均值和方差时，将在 N、H、W上操作，而保留通道C的维度。
如果类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。BN 求均值时，相当于把这些书按页码一一对应地加起来（例如第1本书第36页，第2本书第36页......），再除以每个页码下的字符总数：N×H×W，因此可以把BN看成求“平均书”的操作（注意这个“平均书”每页只有一个字），求标准差时也是同理。
求通道 1 的方差也是同理。对所有通道都施加一遍这个操作，就得到了所有通道的均值和方差。

import torch
x = torch.rand(10, 3, 5, 5)*10000  # NxCxHxW
# 把 channel 维度单独提出来，而把其它需要求均值和标准差的维度融合到一起
x1 = x.permute(1, 0, 2, 3).view(3, -1)  # 维度换位 CxNxHxW，并且view为CxNHW
mu = x1.mean(dim=1).view(1,3,1,1)  # 计算均值，置换为1xCx1x1
std = x1.std(dim=1, unbiased=False).view(1,3,1,1)  # 计算方差，置换为1xCx1x1
my_bn = (x-mu) / std  # 计算标准差

Layer Normalization（LN）：是为了解决BN需要较大batchsize缺点应运而生的Normalization算法。
对其求均值和方差时，将在C、H、W上操作，而保留N的维度。
继续采用上一节的类比，把一个batch的feature类比为一摞书。LN求均值时，相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”，求标准差时也是同理。

x = torch.rand(10, 3, 5, 5)*10000 
x1 = x.view(10, -1)
mu = x1.mean(dim=1).view(10, 1, 1, 1)
std = x1.std(dim=1,unbiased=False).view(10, 1, 1, 1)
my_ln = (x-mu)/std

Instance Normalization（IN）：为了解决风格迁移中，涉及到C维的Normalization会影响迁移，从而设计的不带C维又不依赖batchsize的Normalization算法。
对其求均值和方差时，将在H、W上操作，而保留N、C的维度。
IN 求均值时，相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”，求标准差时也是同理。

x = torch.rand(10, 3, 5, 5) * 10000
x1 = x.view(30, -1)
mu = x1.mean(dim=1).view(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 3, 1, 1)
my_in = (x-mu)/std

Group Normalization（GN）：GN是在复杂任务（如目标分割）中，显存不够不能使用太大batchsize时，LN和IN的折中方案。
对其求均值和方差时，将C维分为G组，在C(G)、H、W维上进行操作，各组C维用对应的归一化参数独立归一化。
继续用书类比。GN相当于把一本C页的书平均分成G份，每份成为有C/G页的小册子，求每个小册子的“平均字”和字的“标准差”。

**x = torch.rand(10, 20, 5, 5)*10000
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
# 把同一 group 的元素融合到一起
x1 = x.view(10, 4, -1)
mu = x1.mean(dim=-1).reshape(10, 4, -1)
std = x1.std(dim=-1).reshape(10, 4, -1)
x1_norm = (x1-mu)/std

之后，大部分Normalization方法都有momentum参数，一般为0.9或0.99.。

running_mean = momentum * running_mean + (1 - momentum) * sample_mean    
running_var = momentum * running_var + (1 - momentum) * sample_var

即当前mean = 0.1 * 当前mean + 0.9 * 以前的mean。
如此处理的原因是如果不加滑动平均，多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了丧失了深度的意义。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift)

Q：简述Batch Normalization。
A：
出现原因：在训练中，分布逐渐发生偏移或者变动，一般是向非线性函数取值上下限两端靠近。产生梯度消失问题，使得网络越深，参数越小，收敛变慢，逐渐导致无法学习。
解决方法：
通过规范化手段，强行将卷积后激活前的分布转变为均值为0方差为1的标准正态分布。
效果：
1. 避免了梯度消失问题，使得分布总是落在非线性函数敏感的输入区间，大大加快了训练速度。
2. 增强分类效果，不用dropout也不容易过拟合。
3. 降低了初始化的随机性，调参更加稳定。
举例：
如果数据整体是左偏的，例如在一个呈现正态分布的数据中95%落在负数区间，此时通过relu激活后，很多参数将因此而置0从而产生梯度消失，而通过BN再进入BN则很好的避免了这个问题。
流程：
1. 求每一个训练批次数据的均值。
2. 求每一个训练批次数据的方差。
3. 使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布。其中ε是为了避免除数为0时所使用的微小正数。
4. 尺度变换和偏移：将xi乘以γ调整数值大小，再加上β增加偏移后得到yi，这里的γ是尺度因子，β是平移因子。
核心思想：
在线性和非线性之间找到较好的平衡点，既能享受非线性的较强表达能力的好处，又避免太靠非线性区两头使得网络收敛速度太慢。
缺点：
由于在N、H、W三个维度上进行操作，使得在batchsize较小的情况下并不能很好的预估数据的真实分布情况，由此诞生了LN。

Q：集成学习方法
A：Bagging类方法：单一模型通过随机构造训练样本、随机选择特征等方法来提高每个模型独立性，代表是随机森林。随机森林进一步引入了随机特征，每个基模型都是决策树。
Boosting类方法：按照一定的顺序先后训练不同的基模型，每个模型都对前序的错误进行单独训练。根据前序的结果，来调整训练样本的权重，从而增加不同模型的差异性。