机器学习笔记

机器学习

---

linear regression

1. 获取一个数据集

数据集一共有m行，每一行是一个example
每一行有n+1列，前n列对应不同的feature，第n+1列是需要预测的值y

2. normalize特征集

使用平均值和标准差来将所有的特征映射到一个统一的比较小的范围，比如-1<=x<=1,这样有助于梯度下降的快速收敛

linear normailze

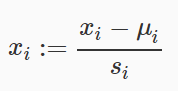
对每一个特征进行这样的操作，ui是特征xi的平均值，si是特征xi的标准差

Polynomial normailze

如果特征是多项式形式的，比如Xi^2,那么先将xi的值平方之后，当成一个独立的变量来进行normailze

3. 构造design matrix

由于需要学习的线性函数如下

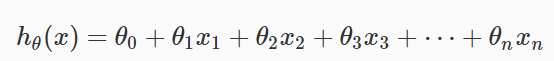
第一项θ0补充一个恒为1的x0来使得形式一致，所以构造一个design matrix

$$\begin{matrix} 1 & x_1^1 & x_2^1 \\ 1 & x_1^2 & x_2^2 \\ 1 & x_1^3 & x_2^3 \\ \end{matrix}$$
使得$h_θ(x)$的计算可以用

来实现

4. 实现cost function

cost function描述了预测值和真实值的差距，定义如下

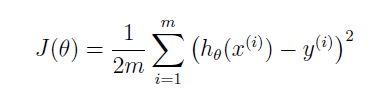
实际计算的时候，可以使用

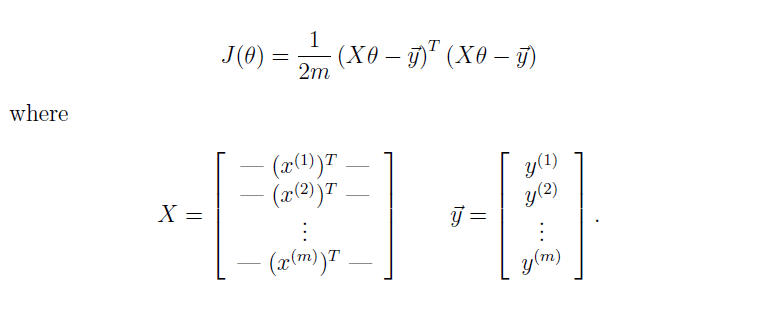
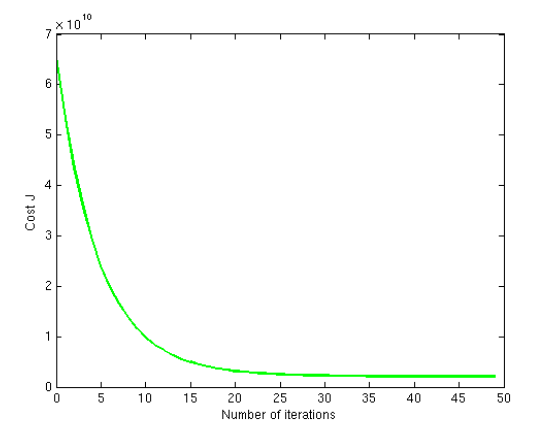
在梯度下降的时候讲cost function在每一轮迭代中迭代的值plot出来是一个研究梯度下降是否收敛和检验学习率α的好方法
cost function的曲线如果出现上升，说明α过大
横轴为迭代次数的时候，可以研究α的大小和收敛速度的关系

5. 梯度下降

梯度下降的原理是，通过计算$J(θ)$的梯度，寻找$J(θ)$下降最快的方向修改θ的值，重复这个过程使得$J(θ)$最小化

需要注意的是$J(θ)$的最小化修改的是θ而不是x和y

梯度下降的更新公式：

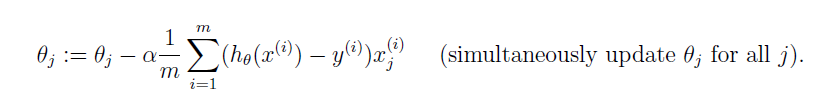
需要注意的是θ必须同时更新，因此可以考虑将这个计算过程向量化

实际计算可以使用这个方程

6. normal equation

不通过梯度下降，直接通过数学方法计算出最小的θ
计算公式如下

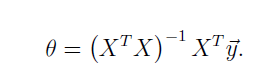
α是学习率，太大可能导致无法收敛，太小可能会收敛过慢
典型值0.1,0.3,0.01,0.03，通过测试选择最好的α

使用梯度下降和normal equation的选择

如果n的值比较小，比如小于10000，那么可以使用normal equation
如果n太大，那么计算矩阵的逆的时间复杂度是$n^3$，开销会过大，使用梯度下降比较合适

7. 验证数据

7.1 normalize

得到测试集的数据时，先将测试集的特征normalize，如果是使用normal equation就不需要

7.2 计算

使用

计算预测值