用蒙特卡罗方法计算定积分

概率论

---

为计算积分

$$J=\int_a^bg(x)dx$$
可采用下面的方法实现。任取一列相互独立的随机变量$\{X_n\}$，它们都服从$[a,b]$上的均匀分布，则$g(X_n)$也是一列相互独立、同分布的随机变量列且
$$E(g(X_n))=\frac{1}{b-a}\int_a^bg(x)dx=\frac{J}{b-a}$$
所以$J=(b-a)E(g(X_n))$，而有大数定律有
$$\frac{g(X_1)+g(X_2)+\cdots+g(X_n)}{n}\stackrel{P}{\longrightarrow}E(g(X_n))$$

因此，只要能生成随机列就能求出$J$ 的近似值，可以在计算机上首先生成服从均匀分布的随机数$\{X_n\}$ ，然后通过上面两式得出近似值，也就是

$$J\approx(b-a)\frac{g(X_1)+g(X_2)+\cdots+g(X_n)}{n}$$

其中，$X_1,X_2,\cdots,X_n$ 是计算机上生成的伪随机数。

用蒙特卡洛方法积分$I=\int_0^1x^3dx$

首先选定一个区间$D=[0,1]$ ，然后抽取4000个随机点的坐标 $(\xi_i,\eta_i)(i=1,2,\cdots,4000)$ ，他们服从区间$D$上的均匀分布。

利用MATLAB生成区间随机掷点效果图

random = unifrnd(0,1,1,4000);%生成4000个区间[0,1]上服从均匀分布的随机数
x=0.00025:0.00025:1;
y=x.^3; subplot(2,1,1),plot(x,y,'k',x,random,'.');
xlabel('x轴'),ylabel('y轴')
for n=1:4000 sumset(n)=0; end
sum=0;
for n=1:4000 sum=sum+random(n).^3; sumset(n)=sum/n;
end subplot(2,1,2),plot(x,sumset);
sum/4000

结果如图

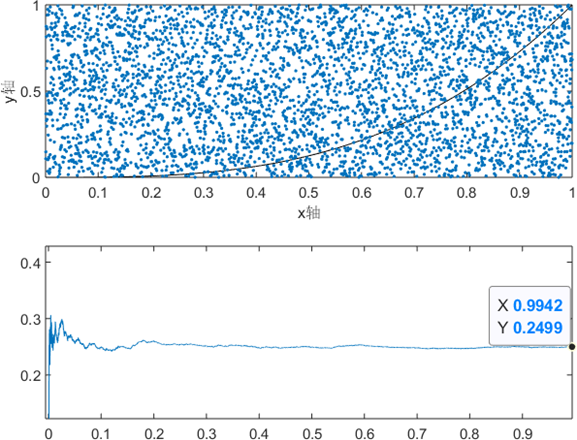
图可知，结果稳定在0.25附近。
有牛顿-莱布尼茨公式可知

$$\int_0^1x^3dx=\frac{1}{4}x^4|_0^1=\frac{1}{4}(1^4-0^4)=\frac{1}{4}$$

模拟值与精确值的误差率为0.129％

用蒙特卡罗方法积分$I=\int_0^1sinx dx$

首先选定一个区间$D=[0,1]$ ，然后抽取4000个随机点的坐标 $(\xi_i,\eta_i)(i=1,2,\cdots,4000)$ ，他们服从区间$D$上的均匀分布。

利用MATLAB生成区间随机掷点效果图

random = unifrnd(0,1,1,4000);%生成4000个区间[0,1]上服从均匀分布的随机数
x=0.00025:0.00025:1;
y=sin(x); subplot(2,1,1),plot(x,y,'k',x,random,'.');
xlabel('x轴'),ylabel('y轴')
for n=1:4000 sumset(n)=0; end
sum=0;
for n=1:4000 sum=sum+sin(random(n)); sumset(n)=sum/n;
end subplot(2,1,2),plot(x,sumset);
sum/4000

结果如图

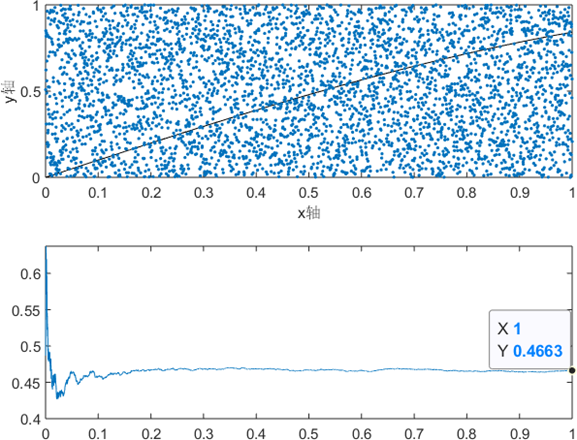
由图可知，结果稳定在0.46附近。

有牛顿-莱布尼茨公式可知

$$\int_0^1sinx dx =-cosx dx|_0^1=-(cos1-cos0)\approx0.45969767413$$