粒子群优化算法

SE

一维的粒子群算法求解

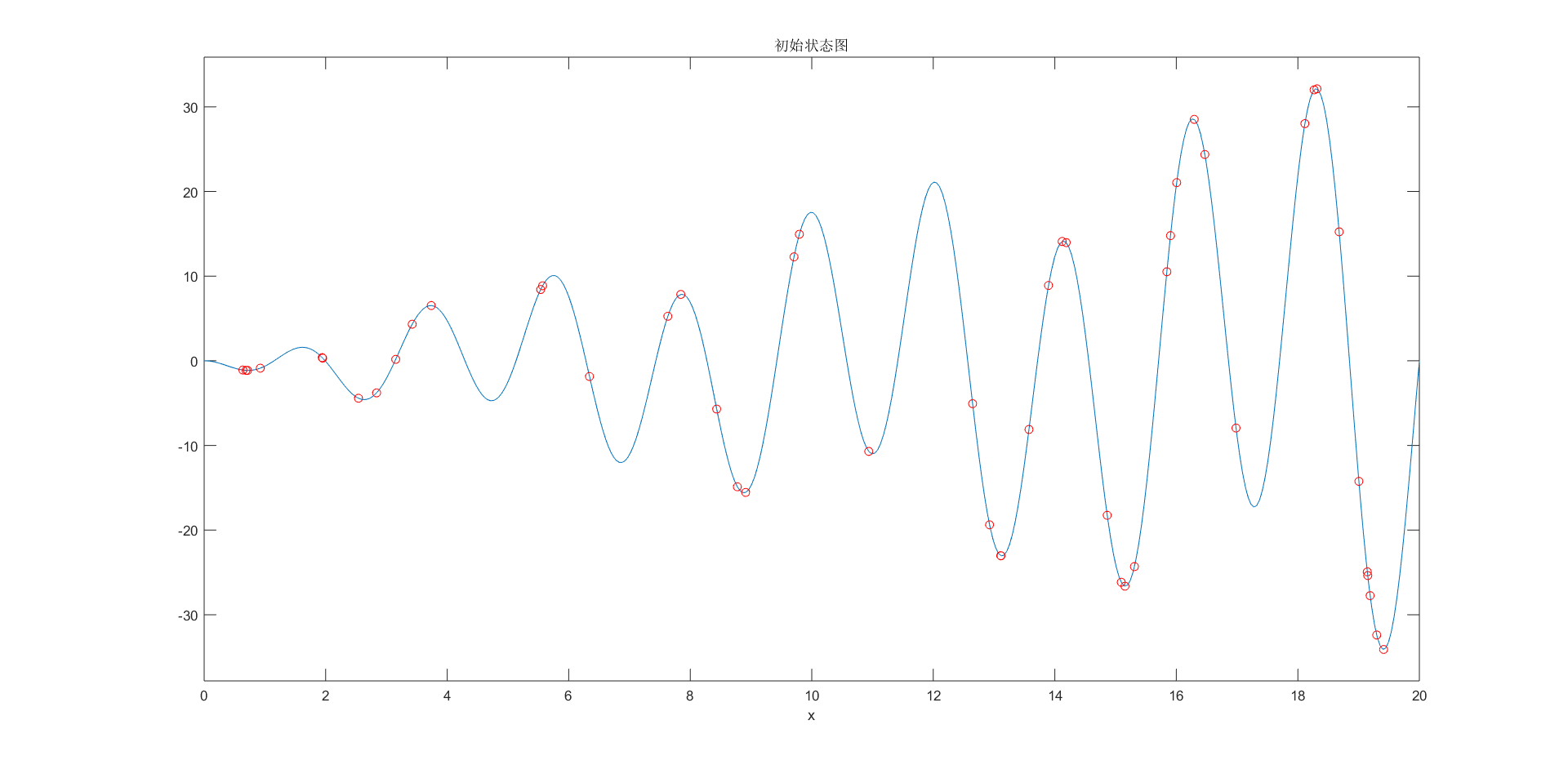
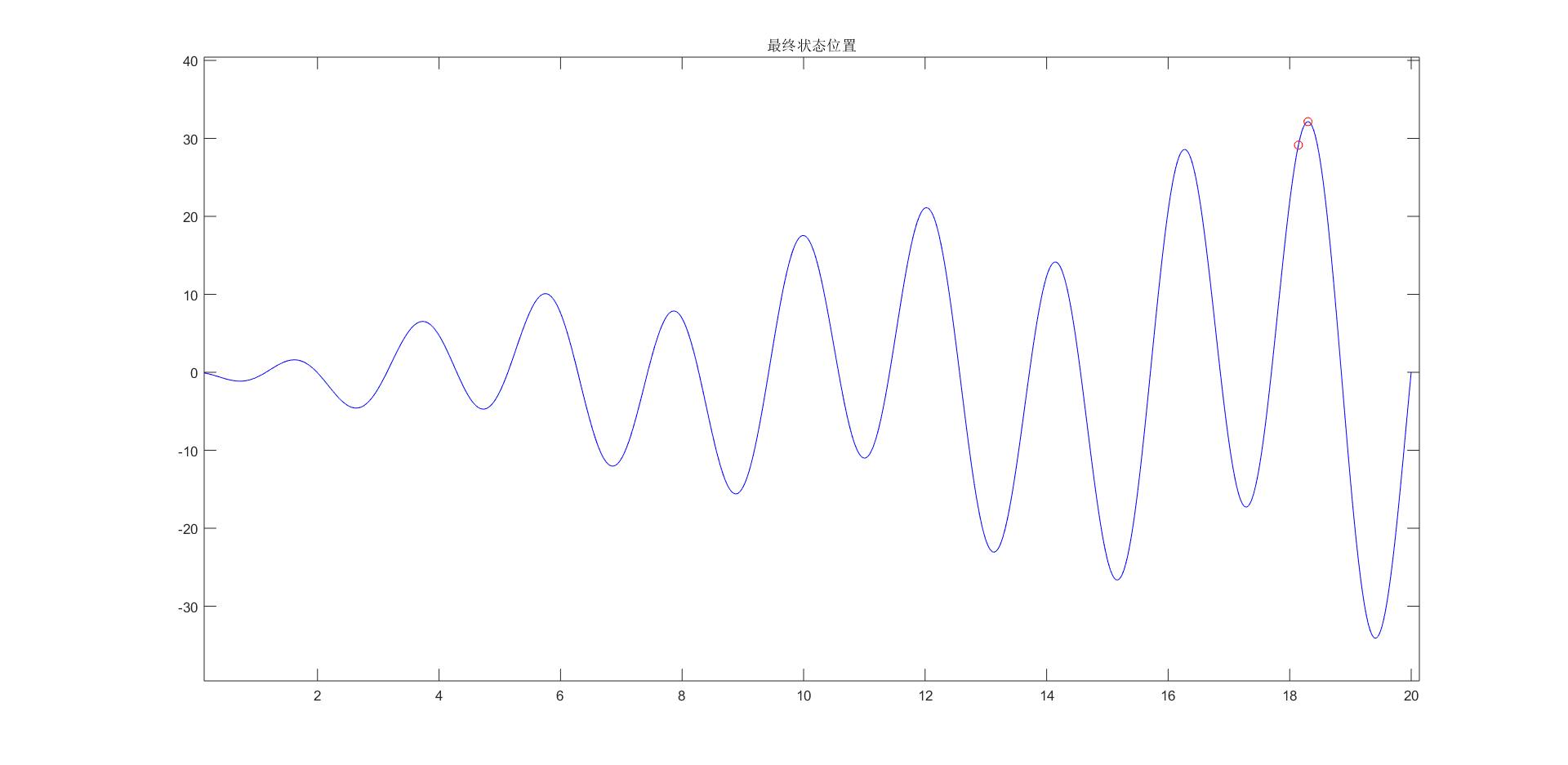
clc;clear;close all;
%% 初始化种群
%已知位置限制[0,20],由于一维问题较为简单，因此可以取初始种群N 为50，迭代次数为100,当然空间维数d 也就是1。位置和速度的初始化即在位置和速度限制内随机生成一个N x d 的矩阵，对于此题，位置初始化也就是在0~20内随机生成一个50x1的数据矩阵，而对于速度则不用考虑约束，一般直接在0~1内随机生成一个50x1的数据矩阵。
%此处的位置约束也可以理解为位置限制，而速度限制是保证粒子步长不超限制的，一般设置速度限制为[-1,1]。
%粒子群的另一个特点就是记录每个个体的历史最优和种群的历史最优，因此而二者对应的最优位置和最优值也需要初始化。其中每个个体的历史最优位置可以先初始化为当前位置,而种群的历史最优位置则可初始化为原点。对于最优值，如果求最大值则初始化为负无穷，相反地初始化为正无穷。
%每次搜寻都需要将当前的适应度和最优解同历史的记录值进行对比，如果超过历史最优值，则更新个体和种群的历史最优位置和最优解。
%点乘对应的是矩阵中元素的相乘,这就需要两个矩阵的维度一定要相同才可以
%函数句柄的写法
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式
figure(1);
ezplot(f,[0,0.01,20]);
% 函数ezplot无需数据准备，可以直接画出函数的图形，画隐函数图形很方便。
N = 50;                         % 初始种群个数
d = 1;                          % 空间维数
ger = 100;                      % 最大迭代次数     
limit = [0, 20];                % 设置位置参数限制
vlimit = [-1, 1];               % 设置速度限制
w = 0.8;                        % 惯性权重
c1 = 0.5;                       % 自我学习因子,一般为2
c2 = 0.5;                       % 群体学习因子 ，一般为2
for i = 1:d
    x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);
   %初始种群的位置,limit表示第一个参数表达式在自变量趋于第二个参数的极限值
end
v = rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = zeros(N, 1);               % 每个个体的历史最佳适应度
fym = -inf;                      % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态图');
% figure(2)
%% 群体更新
iter = 1;
record = zeros(ger, 1);          % 记录器
while iter <= ger
     fx = f(x) ; % 个体当前适应度   
     for i = 1:N      
        if fxm(i) < fx(i)
            fxm(i) = fx(i);     % 更新个体历史最佳适应度
            xm(i,:) = x(i,:);   % 更新个体历史最佳位置
        end 
     end
if fym < max(fxm)
        [fym, nmax] = max(fxm);   % 更新群体历史最佳适应度,
%         该方法能够记录下每列的最大值和其对应的索引位置
        ym = xm(nmax, :);      % 更新群体历史最佳位置
 end
    v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
    % 边界速度处理
    v(v > vlimit(2)) = vlimit(2);
    v(v < vlimit(1)) = vlimit(1);
    x = x + v;% 位置更新
    % 边界位置处理
    x(x > limit(2)) = limit(2);
    x(x < limit(1)) = limit(1);
    record(iter) = fym;%最大值记录
%     x0 = 0 : 0.01 : 20;
%     plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
%     pause(0.1)
    iter = iter+1;
end
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
hold off
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值：',num2str(fym)]);
disp(['变量取值：',num2str(ym)]);