@TangWill 2019-06-21T13:12:46.000000Z 字数 6470 阅读 1305

北京二环路立交桥桥面限流问题的研究

`数学建模`

摘要

本文探究的是在立交桥面两端设置交通信号灯控制机动车进出立交桥这一方案，对缓解北京二环路的拥堵问题的可行性。通过收集北京二环开放交通数据，并对该措施建立立交桥的红绿灯调节模型进行分析，从而得出结论。

问题一，首先从北京交通发展研究院公布的官方数据获得了2017年主要道路交通流量，并通过收集两天该机构公布的实时路况数据，对北京二环路工作日的平均机动车流量进行模型预估和测试，并根据交通指数获得出现道路拥堵的时段信息。

问题二，在对典型立交桥环境建立交通模型和修改后，根据问题二建立恰当的数学模型。对问题一收集到的北京二环路高峰时期数据进行预处理，在问题一的模型基础上，建立新的交通流量与速度的数学模型，从而求得交通信号灯控制限流对立交桥桥面交通流量和拥堵时间段的影响。

问题三，在问题二的基础上，对北京二环路个拥堵的立交桥两端实施交通信号灯控制机动车进出的问题可以等价于在无交通信号灯控制机动车进出的环境下，增加一个有交通信号灯的立交桥模型，即在求得问题二结果下再次使用问题二的模型，并求得新环境对立交桥桥面交通流量和拥堵时段的影响。

问题四，在前三个问题的探究过程中，交通流量与机动车行驶速度的数学模型是探究交通信号灯对立交桥桥面限流有着重要意义。在解决前三个问题的基础上，对上述模型进行修改，进而得到立交桥限流对与北京二环路相连通的其他道路拥堵情况的影响。

关键词：立交桥限流，交通指数，交通限流、速度、密度

一、问题重述

城市道路交通问题是一个复杂的社会系统工程，它不仅与市民的生活密切相关，而且关系到经济的发展和社会的进步。随着经济的高速发展和城市化进程的加快，机动车拥有量急剧增加。道路交通拥挤已成为众所周知的“都市顽疾”。为解决这一问题，在城市规划的过程中，立交桥开始出现，这在一定程度上缓解了拥堵状况。但近年来，车辆激增的速度更快，全面性的拥堵变得非常普遍，交通高峰时候的拥堵更是不可避免。现在我们就北京二环路的交通现状，应用数学建模的方法提出、分析并探讨在立交桥面两端设置交通信号灯控制机动车进出立交桥这一方案对缓解道路交通拥堵问题的可行性。

下图是立交桥的组成示意图，在本文要解决的环境下，在下图模型所示的立交桥入口和出口处各添加一个红绿信号灯。

图1-1 立体交叉口组成示意图

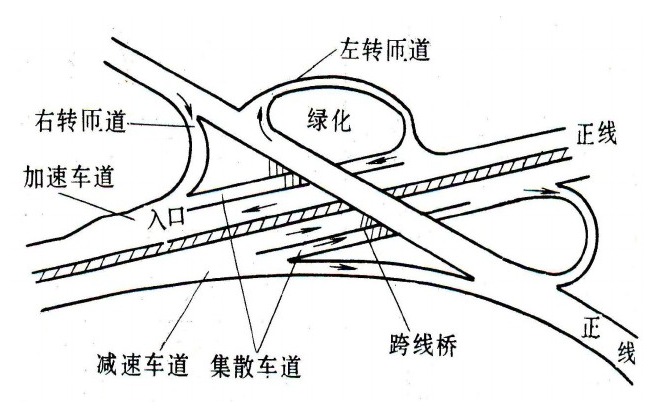
本文在上述环境中解决下列问题：
(1) 根据北京二环路交通数据，给出北京二环路工作日的平均机动车流量和出现道路拥堵的时段；
(2) 在对上述交通模型作添加红绿信号灯的修改后，预估工作日的平均机动车流量和出现道路拥堵的时段会发生的变化；
(3) 对北京二环路上两个拥堵的立交桥进行问题(2)的模型修改，并重复问题(2)工作；
(4) 研究修改后的交通模型对二环路其他道路的影响。

二、模型假设

(1) 假设车的平均长度为当前行驶速度的安全车距，且车的长度对交通没有影响；
(2) 假设所有的司机都遵守交通规则，没有交通事故发生；
(3) 不考虑汽车发动时间和制动时间的影响；
(4) 不考虑天气和车辆状况的影响；
(5) 汽车在立交桥上匀速行驶
(6) 假设汽车之间间距以及汽车均为标准小汽车；(7)汽车行驶速度在每十五分钟的变化都是均匀的。

三、问题分析

3.1 交通拥堵的概念

交通拥堵是指一定时间内道路的承载能力不能满足车辆的通行要求，即道路上的车流量大于道路的最大车流量，是超出部分滞留在路上的交通现象。

下面为交通资源占用情况的数学模型

$\begin{align}R=k \times T\tag 1\end{align}$

其中， $k$ 为车身长度加车间安全距离， $T$ 为车辆在行车道上行驶的平均总时间。我们可以从中得出结论，解决拥堵的方式可归结为两种：(1) 减少资源占用时间；(2) 合理增加资源总量。立交桥也是为满足以上两点而产生的。

3.2 立交桥的地位

城市人口的急剧增加使车辆日益增多，平面立交的道口造成车辆堵塞和拥挤。需要通过修建立交桥和高架道路形成多层立体的布局，以提高车速和通过能力。广泛应用于高速公路和城市道路中的交通繁忙地段。在一定程度上缓解了交通的拥堵情况。

但立交桥也有线路迂回较长，行车方案可选择性较少等缺点。尤其是在近年来机动车拥有量急剧增加，其无流量控制的缺点显得尤为突出，城市道路交通拥堵问题亟待解决。为此，可以在立交桥两端加红绿灯，从而实现流量控制。

3.3 红黄绿信号灯转换方法

以北京市朝阳区某4个连续交叉口为研究对象，在调查数据的基础上，平峰时等比例将个交叉口的信号配时方案调整为100s，高峰时等比例将各交叉口的信号配时方案调整为120s。按照此信号灯转换方法，对立交桥桥面两端红绿灯转换机制进行设计。

四、符号说明

表4-1 符号说明

符号	解释
$Q$	流量，辆/h
$K$	密度，辆/公里
$V$	区间平均速度，km/h
$N$	车辆数，辆
$L$	路段长度，km
$V_1$	入口速度，km/h
$V_2$	出口速度，km/h
$n$	车辆最大并排数，辆
$l$	车辆间距加长度
$t$	时间段，每15分钟（单位时间）
$K_j$	交通拥堵时的车流量密度,辆/公里
$V_f$	畅通行驶时的车速，km/h
$T$	红绿灯周期，s
$t_1$	绿灯时长，s
$V_3$	其他道路的入口处的车速，km/h
$V_4$	其他道路出口处的车速,km/h

五、模型的建立与求解

模型一、通过行车速度的数学期望与车辆密度预估平均机动车流量

交通流量、速度、密度是描述交通流基本特征的三个主要参数，它们之间相互联系、相互制约。交通流近似看作是由交通体组成的一种粒子流体，同其他流体一样，可以用交通流量、速度和密度三个基本参数来描述。

$\begin{align}Q=K \times V\tag 2\end{align}$
式中，

$Q——$ 流量，辆/h，

$K——$ 密度，辆/公里，

$V——$ 区间平均速度，km/h。

图5-1

$Q=K \times V$ 交通流模型曲线图

首先，在北京交通发展研究院发布的《2018年北京交通发展年报》中，获得如下数据：

表5-1 2017年主要道路交通流量（部分）

路段	全天路段平均流量（标准车）	高峰时段（7-9点）路段平均流量（标准车）
东二环路	229707	28908
西二环路	231969	28016

同时，对北京交通发展研究院公布的实时路况数据进行收集（数据每15分钟更新），共收集两个工作日的有效数据，如下：

图5-2 2019年4月28日、4月29日北京二环路平均速度统计

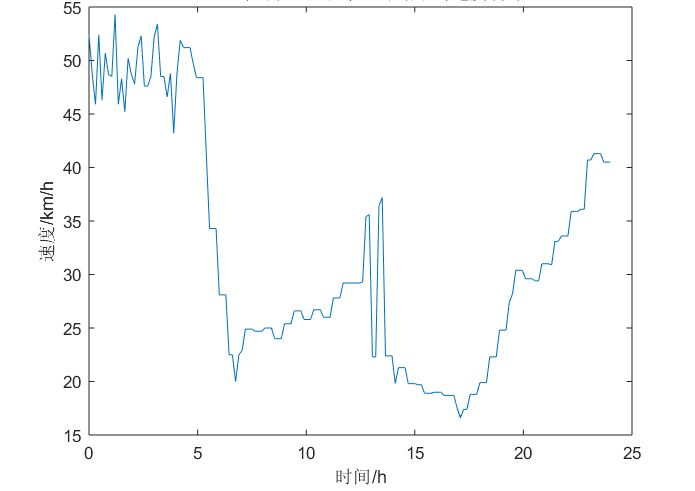
$\qquad \quad$ untitled.png-20.2kB

对收集到的数据筛选、处理，得到如下结果：

表5-2 数据预处理结果

速度 $(km/h)$	频数	频率	相对安全距离(m)
$\leq20$	26	0.161491	10
$20\sim 40$	90	0.559006	30
$40\sim 50$	32	0.198758	50
$50 \sim 60$	13	0.080745	80

（注：区间划分依据：不同速度的相对安全距离不同）

由

$\begin{align}E(x)=\sum^\infty_{k=1}x_kp_k\tag 3\end{align}$
求得北京二环路工作日的机动车速度期望为

$31.77km/h$ 。查表可知，车身长度及车间安全距离近似为

$30.5$ 米，标准车平均宽度

$2.3$ 米。根据官方数据，北京二环路长

$32.7$ 公里，平均宽度

$24.4$ 米，由

$\begin{align}K=\frac{N}{L}\tag 4\end{align}$
计算得工作日北京二环路单位长度车道上某一瞬间所存在的车辆数为

$K \approx298.84$ 辆。

最后，根据之前建立的模型，对北京二环路工作日的平均机动车流量进行预估，得到结果 $Q=9494.091$ （辆/小时），则全天路段平均流为227858.2辆，与2017北京交通发展研究院公布的2017年统计数据基本一致。

此外，在这里我们引入交通指数的概念，交通指数是道路交通运行指数（也成道路交通）的简称交通运行指数是综合反映道路网交通运行情况的指标。它是通过分布在城市各条道路的运行车辆实时、动态地获得每一条道路在该时刻的行程速度，并通过无线通信网络实时上报数据处理中心；数据处理中心从全路网（覆盖五环内的主城区）整体的角度出发，按照道路上通过的车辆越多则其在全路网评价中权重越大的原则，通过对每一条道路加权集成，得出路网整体或者交通走廊、重点功能区的交通拥堵特征数据；再根据出行者对交通拥堵的感知判断，依据大量现场调查数据的聚类分析，将交通拥堵特征数据转换为单一化的交通指数。

表5-3 交通指数

指数	说明
0~2	畅通：交通运行状况良好，基本没有道路拥堵
2~4	基本畅通：交通运行状况较好，有少量道路拥堵
4~6	轻度拥堵：交通运行状况较差，部分环路、主干路拥堵
6~8	中度拥堵：交通运行状况差，大量环路、主干路拥堵
8~10	严重拥堵：交通运行状况很差，全市大部分道路拥堵

通过对北京二环路和全路网交通指数的收集，得到如下结果。

图5-3 2019年4月28日交通指数统计结果

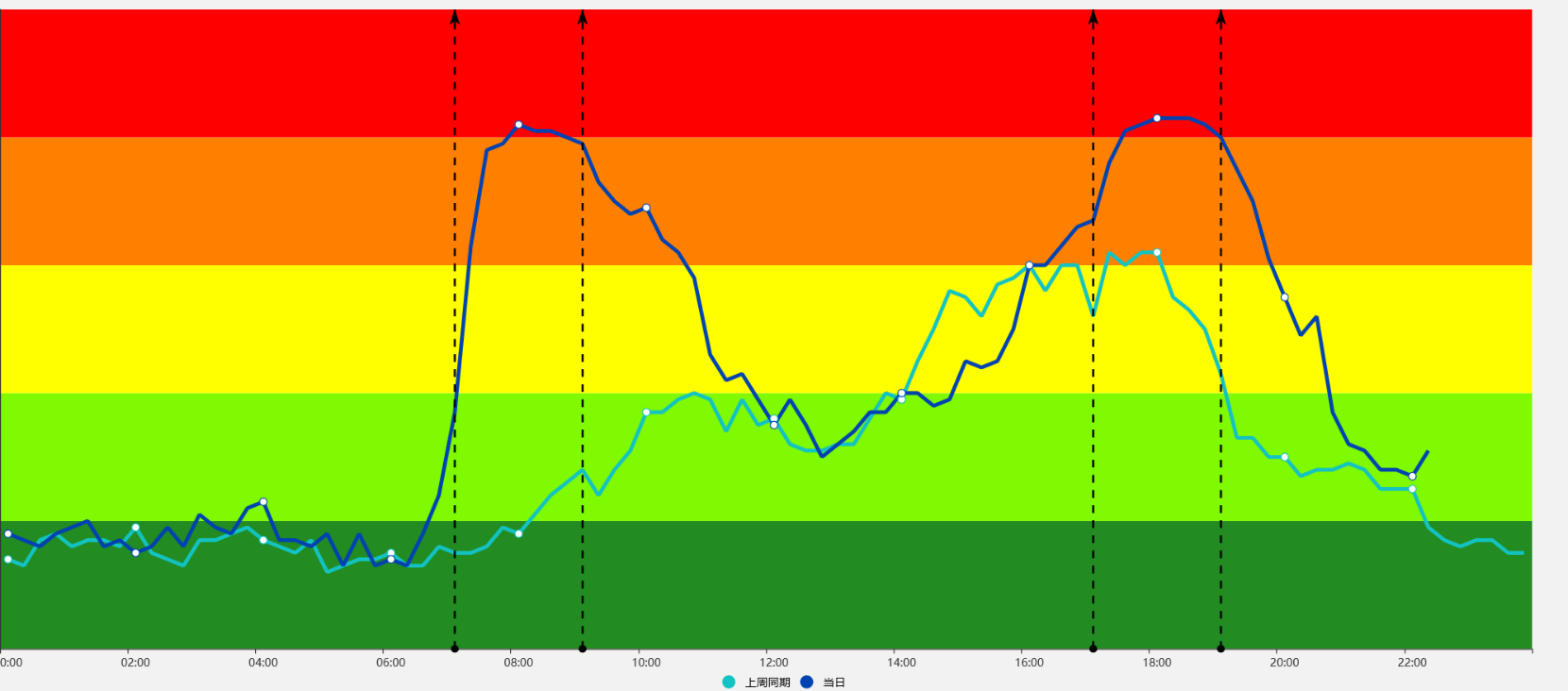
echarts (1).png-120.5kB

从而得出发生拥堵的时间段为早高峰7时到9时和晚高峰17时到19时。

模型二、加入红绿灯后汽车立交桥高峰时段以及车流量的变化

未加红绿灯前：

$\begin{align}Q=K_j\times (V-\frac{V^2}{V_f})\tag 5\end{align}$
由交通指数可知

$V_f=30km/h;K_j=n\times1000m/l$ ;在道路拥挤时，由安全距离可知

$l=10m$ 。

相邻两个点

$\begin{align}Q[i]-Q[i-1] = (\frac{n}{l})\times(V_1-V_2)\tag 6 \end{align}$
即表示单位时间内立交桥上车辆数变化。

加入红绿灯后：

立交桥上车辆数变化

$\begin{align}\Delta Q=(\frac{n}{l})\times(V_1\times \frac{t_1}{T} - V_2) \tag 7\end{align}$

$V_1\times \frac{t_1}{T}——$ 相当于红灯时速度与绿灯时速度的加权平均，红灯时速度为0，绿灯时为

$V_1$ 。

利用c++程序对采集到的数据早高峰7时到9时进行数据模拟，可以得知，立交桥拥堵将持续一个小时，即拥堵时间段为7时到8时，同理，晚高峰为15时到16时。

模型三、加入两个红绿灯对立交桥限流后汽车立交桥高峰时段以及车流量的变化

由(5),(6),(7)可得

$\begin{align}\Delta Q=\frac{n}{l}\times(\frac{t_1}{T}-1)\times V_1 +K_j\times(V_i-\frac{V_i^2}{V_f}-V_{i-1}+\frac{V_{i-1}}{V_f}) \tag 8\end{align}$

由模型可得，对两个立交桥进行交通信号灯限流，并不影响立交桥拥堵时段，即拥堵时间段为7时到8时和晚高峰为15时到16时。

模型四、通过拥堵时段的行车速度均值与交通流量预估立交桥限流对与二环路相连通道路的影响

将整个二环路看成一个圆，而立交桥是圆上的一截，而其他道路可视作圆上除去这一截的部分，立交桥的入口处等价于其他道路的出口，立交桥的出口等价于其他道路的入口，所以探究设置红绿灯对其他道路的影响，可以视作在其他道路的出口处设置红绿灯机制。

而这种设置与第（2）问的模型假设有相似之处，即设置红绿灯的路段的车流速度按照加权平均，红灯时车速为0，则

$\begin{align}v'=\frac{(v\times t_1+0\times t_2)}{T}=\frac{v\times t_1}{T}\tag 9\end{align}$

则

$\begin{align}v3=v2\tag {10} \end{align}$

$\begin{align}v4=v1\tag {11}\end{align}$

（ ） （ ）

$Q[i+1]-Q[i]=\frac{n}{L}\times（V_3-V_4）=\frac{n}{L}\times（V_2-V_1）\tag {12}$

设置红绿灯后

$Q[i+1]-Q[i]=\frac{n}{L}\times(V_2-\frac{t_1}{T}\times V_1) \tag{13}$

这样求解出来的斜率实际上是第二问的相反数，即每一单位时间段的斜率都是对应时间段中第二问的斜率的相反数，即当立交桥设置红绿灯后，相当于其他路段的出口被设置了红绿灯限制出行，但其他路段的入口车辆照常行驶，这使得其他路段的变得比设置红绿灯前更拥堵。

六、模型评价

在模型一中，以官方公布的数据为样本数据，收集到的工作日数据作为测试数据，并将机动车类比为微观粒子，从而将收集到的速度数据与流量建立数学模型。但是，由于收集到的有效测试数据较少，缺乏对模型进行完善的指标。

在模型二中，很好的建立起交通流量与速度的关系，便于求解交通流量的变化，由于数据的离散型，不易给出准确的数值变化。

在模型三中对模型二进行修改和进一步的探究，有助于解决问题。

在模型四中，由于数据的缺少，暂时不能验证模型的准确定，可以作为进一步的研究工作。

参考文献

[1]北京交通发展研究院.道路交通系统运行[J].2018年北京交通发展年报,2018,1:51-54.

附录

程序1

import itchat
import re
import urllib.request
import time
import chardet
itchat.login()
def getHtm(url):
    page = urllib.request.urlopen(url)
    html = page.read()
    return html
i = 0
def getImg1(html):
    reg1 = r'<td>+(?!&nbsp)(.+)</td>+'
    imgre1 = re.compile(reg1)
    imglist1 = re.findall(imgre1, html)
    for line in imglist1:
        if line.startswith("&"):
            imglist1.remove(line)
    return imglist1
def getImg2(html):
    reg2 = r"([0-9]+:[0-9]+-[0-9]+:[0-9]+)&nbsp;&nbsp;"
    imgre2 = re.compile(reg2)
    imglist2 = re.findall(imgre2, html)
    return imglist2
while (True):
    html = getHtm(r'http://www.bjjtw.gov.cn/uservice/app/congestion/serviceCongestion')
    encode_type = chardet.detect(html)
    html = html.decode(encode_type['encoding'])  
    list2 = getImg2(html)
    i = 0
    for a in list2:
        data = str(a)
    for line in list1:
        if ((i + 1) > 4 and (i + 1 < 9)):
            line + ','
            if ((i + 1) % 4 == 0):
                itchat.send(data, 'filehelper')
            itchat.send(line + ',', 'filehelper')
        i += 1;
    time.sleep(300)

程序2

#include <iostream>
#include <cmath>
using namespace std;
int main() {
    double a[36]={19.7,18.9,18.9,18.9,19,19,19,18.7,18.7,18.7,18.7,17.5,16.6,17.4,17.4,18.8,18.8,18.8,19.9,19.9,19.9,22.3,22.3,22.3,24.8,24.8,24.8,27.4,28.2,30.4,30.4,30.4};
    double b[35];
    double sum=30;
    for(int i=1;i<35;i++) {
        b[i - 1] =-1/15*(a[i]+a[i-1])/2+1600*(a[i]-a[i-1])+160/3*(pow(a[i-1],2)-pow(a[i],2));
    }
    for(int i=1;i<35;i++)
    {
        if(sum<22) {
            cout << i;
            break;
        }
        sum+=b[i];
    }
    return 0;
}