Theorem and Algorithm

DiscreteMathematicalStructures

---

Theorem

---

Chapter 1

---

Theorem 1

If A,B and C are finite sets, then
$|A\bigcup B|=|A|+|B|-|A\bigcap B|$
$|A\bigcup B \bigcup C|=|A|+|B|+|C|-|A\bigcap B|-|B \bigcap C |-|A \bigcap C|+|A\bigcap B \bigcap C|$

Theorem 2

$f_{A \bigcap B}(x)=f_A(x)\cdot f_B(x)$
$f_{A \bigcup B}(x)=f_A(x)+f_B(x)-f_A(x)\cdot f_B(x)$
$f_{A \bigoplus B}(x)=f_A(x)+f_B(x)-2f_A(x)\cdot f_B(x)$

Theorem 3

If A, B, and C are Boolean matrices of compatible sizes, then
$(A\bigodot B)\bigodot C=A\bigodot (B\bigodot C)$

---

Chapter 2

---

key word:Tautology、Contradiction、Contingency

Theorem 1

$p \iff q \equiv(p\implies q)\bigwedge(q \implies p)$
$p\iff q\equiv (\sim p \bigvee q)\bigwedge (\sim q \bigvee p)$
$p\iff q \equiv (p\bigwedge q )\bigvee (\sim q \bigwedge \sim p)$

---

Chapter 4

---

Theorem 1

If both A and B are finite sets then
$| A\times B | = | A | \times | B |$

Theorem 2

Let R and S be relations from A to B. If R(a)=S(a) for all a in A, then R=S.

Theorem 3

A relation R is transitive if and only if it satisfies the following property: If there is a path of length greater than 1 from vertex a to vertex b, there is a path of length 1 from a to b (that is, a is related to b). Algebraically stated, R is transitive if and only if $R^n\subseteq R$ for all $n\geq 1$.

Theorem 4

Let P be a partition of a set A. Recall that the sets in P are called the blocks of P . Define the relation R on A as follows:
aRb if and only if a and b are members of the same block.
Then R is an equivalence relation on A.

Theorem 5

Let R be an equivalence relation on A, and let P be the collection of all distinct relative sets R(a) for $a\in A$. Then P is a partition of A, and R is the equivalence relation determined by P .

Theorem 6

Suppose R and S are relations from A to B.
If $R \subseteq S$,then $R^{-1}\subseteq S^{-1}$
If $R \subseteq S$,then $\bar{S}\subseteq \bar{R}$
$(R \bigcap S)^{-1}=R^{-1}\bigcap S^{1}$ and $(R\bigcup S)^{-1}=R^{-1}\bigcup S^{-1}$
$\over{R \bigcap S}$$=$$\bar R \bigcup \bar S$ and $\over{R \bigcup S}$$=$$\bar R \bigcap \bar S$

Theorem 7

Let R and S be relations of a set A.
If R is reflexive, so is $R^{-1}$.
If R and S are reflexive, then so are $R\bigcap S$ and $R \bigcup S$.
R is reflexive if and only if $\bar R$ is irreflexive.

Theorem 8

Let R be a relation on a set A. Then
R is symmetric if and only if $R=R^{-1}$.
R is antisymmetric if and only if $R\bigcap R^{-1}\subseteq \Delta$.
R is asymmetric if and only if $R \bigcap R^{-1}=Ø$.

Theorem 9

R is reflexive if and only if $\Delta \subseteq R$.
R is irreflexive if and only if $R \bigcap \Delta =Ø$.
R is transitive if and only if $R^2 \subseteq R$.
R is transitive if and only if $R^n \subseteq R$, for any $n \geq1$.

Theorem 10

Let R and S be relations on A.
If R is symmetric, so are $R^{-1}$ and R.
If R and S are symmetric, so are $R \bigcap S$ and $R \bigcup S$.

Theorem 11

Let R and S be relations on A.
$(R \bigcap S)^2\subseteq R^2\bigcap S^2$
If R and S are transitive, so are $R \bigcap S$.
If R and S are equivalence relations, so are $R\bigcap S$.

If R and S have the properties	$\bar R$	$R^{-1}$	$R \bigcap S$	$R \bigcup S$	S◦R
Reflexive	Irreflexive	1	1	1	1
Irreflexive	Reflexive	1	1	1	0
Symmetric	1	1	1	1	0
Antisymmetric	1	1	1	1	0
Transitive	0	1	1	0	0
Equivalence	0	1	1	0	0

Theorem 12

Let R be a relation from A to B, and let S is a relation from B to C. Then if $A_1$ is any subset of A, we have

$$(S◦R)(A_1)=S(R(A_1))$$

Theorem 13

Suppose that A, B, C, and D are sets, R is a relation from A to B, S is a relation from B to C ,and T is a relation from C to D. Then

$$T◦(S◦R) = (T◦S)◦R$$

Theorem 14

Suppose that A, B and C are sets, R is a relation from A to B, and S is a relation from B to C. Then

$$(S◦R)^{-1} = R^{-1}◦S^{-1}$$

Theorem 15

If R and S are equivalence relations on a set A, then the smallest equivalence relation containing both R and S is $(R \bigcup S)^\infty$

---

Chapter 5

---

Theorem 1

Let f : $A\to B$ be a function.
Then $f^{-1}$ is a function from B to A if and only if f is one to one.
Let f : $A\to B$ be a function. If $f^{-1}$ is a function, then
the function f -1 is also one-to-one.
$f^{-1}$ is everywhere defined if and only if f is onto.
$f^{-1}$ is onto if and only if f is everywhere defined .

Theorem 2

Let f : $A\to B$ be a function.
$1_B◦ f=f$
$f◦1_A=f$

Theorem 3

If f : $A\to B$ is a one-to-one correspondence between A and B, then
$f^{-1}◦f=1_A$
$f◦f^{-1}=1_B$

Theorem 4

Let f : $A\to B$ and g : $BA$ be functions such that g◦f =1_A$ and f◦g=1B. Then f is a one-to-one correspondence between A and B, g is a one-to-one correspondence between B and A, and each is the inverse of the other.

Let f : $A\to B$ and g : $B\to C$ be invertible. Then g◦f is invertible, and $( g◦f )^{-1}=f^{ -1}◦g^{ -1}$.

---

Chapter 6

---

Theorem 1

If $(A, \leq)$ and $(B, \leq)$ are posets, then $(A \times B, \leq)$ is a poset, with the partial order $\leq$ defined by

$$(a, b)\leq(a’, b’)$$
if $a\leq a’$ in A and $b\leq b’$ in B

Theorem 2

Let A be a finite nonempty poset with partial order $\leq$. Then A has at least one maximal element and at least one minimal element

Theorem 3

A poset has at most one greatest element and at most one least element.

Theorem 4

Let $(A, \leq)$ be a poset. Then a subset B of A has at most one LUB and at most one GLB.

---

Chapter 7

---

Theorem 1

Let $(T, v_0)$ be a rooted tree. Then
There are no cycles in T .
$v_0$ is the only root of T.

Theorem 2

Let R be a symmetric relation.
The following statements are equivalent.
(a) R is an undirected tree.
(b) R is connected and acyclic.
(c) R is acyclic, and if any undirected edge is added to R, the new relation will not be acyclic.
(d) R is connected, and if any undirected edge is removed from R, the new relation will not be connected.

Theorem 3

Let R be a symmetric relation on a set A, |A|=n is finite.
The following statements are equivalent.
(a) R is an undirected tree.
(b) R is connected and has n-1 edges.
(c) R is acyclic and has n-1 edges.

---

Chapter 8

---

Theorem 1

(a) A graph G has an Eulerian circuit if and only if G is connected and every vertex has even degree.
(b) A graph G has an Eulerian path if and only if either all, or all but two vertices, the two endpoints, have an even degree.

Theorem 2

simple graph with n vertices $(n \geq 3)$ is Hamiltonian if each vertex has degree n/2 or greater

Theorem 3

A graph with n vertices $(n \geq 3)$ is Hamiltonian if, for each pair of non-adjacent vertices, the sum of their degrees is n or greater .

Theorem 4

Let the number of edges of G be m. then G has a Hamiltonian circuit if $m\geq \frac{(n^2-3n+6)}{2}$.

---

Algorithm

---

Warshall's Algorithm

1.CLOSURE $\leftarrow$ MAT
2.FOR K=1 THRU N
$\quad$a. FOR I = 1 THRU N
$\qquad$1. FOR J = 1 THRU N
$\qquad \quad$a. CLOSURE[I,J]$\leftarrow$CLOSURE[I,J]$\bigvee$ (CLOSURE[I,K] $\bigwedge$ CLOSURE[K,J])

Warsheall算法直观应用

• 第k次
  
  • 第k行不为0元素所在列画直线，
  • 第k列不为0元素所在行画直线，
  • 直线相交位置如果为0，则改为1

topology ordering Algorithm

For finding a topological sorting of a finite poset $(A,\leq)$

Step 1 Choose a minimal element a of A
Step 2 Make a the next entry of SORT and replace A with A-{a}.
Step 3 Repeat steps 1 and 2 until A ={}

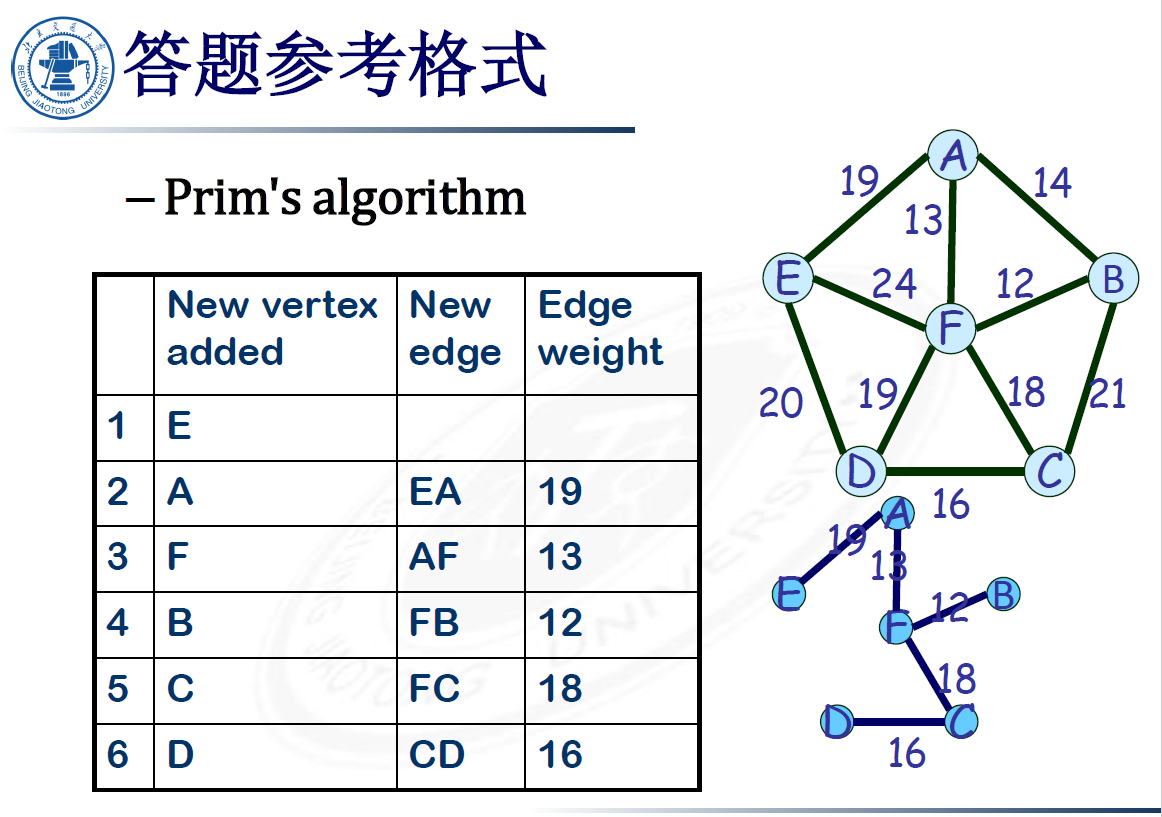
Prim’s Algorithm

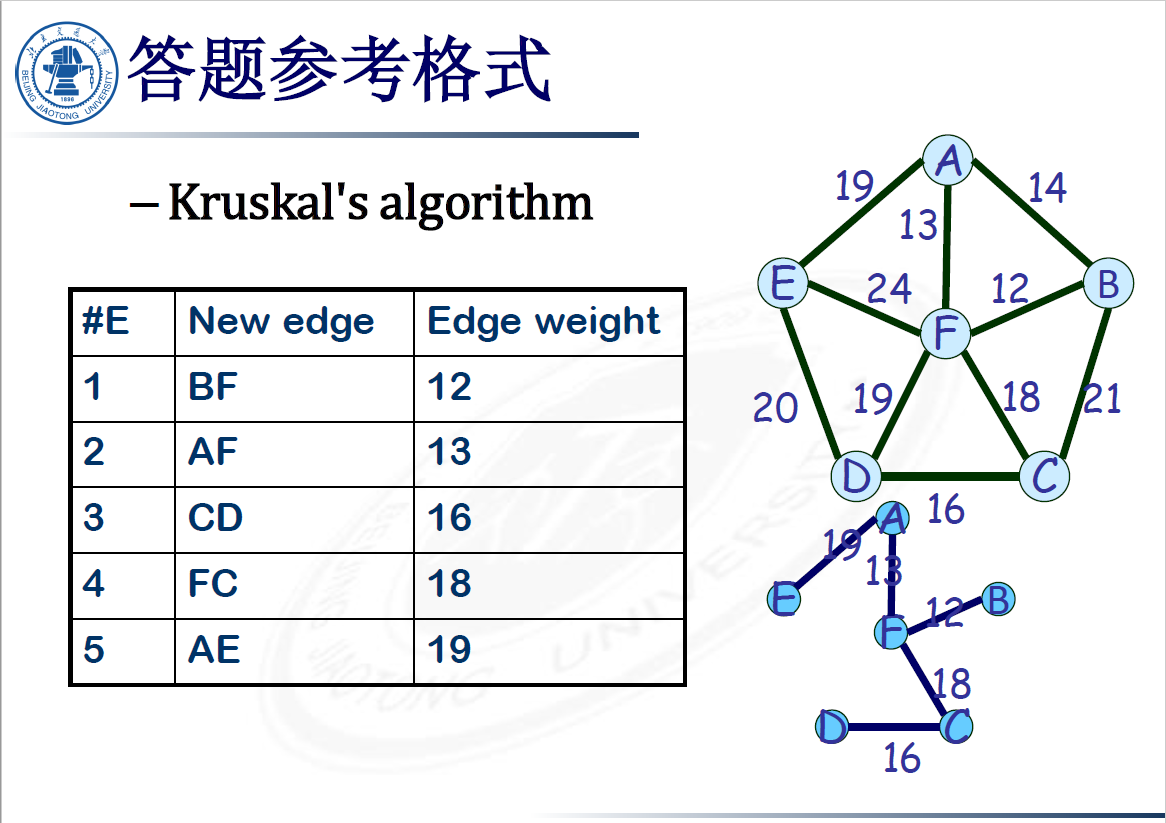
Kruskal’s Algorithm

Dijkstra’s Algorithm

T(v) = min{ T(u)+|uv| } for all $u\in V$ and u is adjacent to v.

Fleury's Algorithm

We start with a vertex of odd degree—if the graph has none, then start with any vertex.

At each step we move across an edge which is not a bridge, unless we have no choice, then we delete that edge.

At the end of the algorithm there are no edges left, and the sequence of edges we moved across forms an Eulerian circuit if the graph has no vertices of odd degree or an Eulerian path if there are two vertices of odd degree.

Welsh–Powell algorithm

order the vertices according to their degrees as $v_1,\cdots,v_n$ and assigns to $v_i$ the smallest available color not used by $v_i’s$ neighbours among $v_1,\cdots, v_i-1$, adding a fresh color if needed.