相机标定和结构光编码

大创

---

1、相机标定

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

---

1.1、相机模型

---

摄像机的光学原理成像最早见于春秋时期《墨子》一书，书中提到“景到，在午有端，与景长。说在端。”“景。光之人，煦若射，下者之人也高；高者之人也下。足蔽下光，故成景于上；首蔽上光，故成景于下。在远近有端，与于光，故景库内也。” 该段文字简单的描述了光沿直线传播，在通过一个小孔以后可以在背面成像的事实。中国古代对很多方面自然科学都有记载和描述（例如力学上的胡克定律等），可惜的是很多都没有形成系统的科学。之后就是意大利的波尔塔在《自然魔术》的书中的描述的利用暗箱来写生的时期，其实就是简单的小孔成像模型，但是当时没有成像的介质，所以只能用手工的形式进行记录。所以之后摄像机的演变大都是在记录介质上的改善，从涂有感光性沥青的锡基底版，到溴化银感光材料涂制的干版，到我们熟悉的胶卷，到现在普遍使用的 CCD 感光阵列，摄像机的发展经历大概三个阶段。

摄像机成像原理就是利用光沿直线传播的光学特性来对物体进行成像的。下面将简单的介绍小孔成像模型：

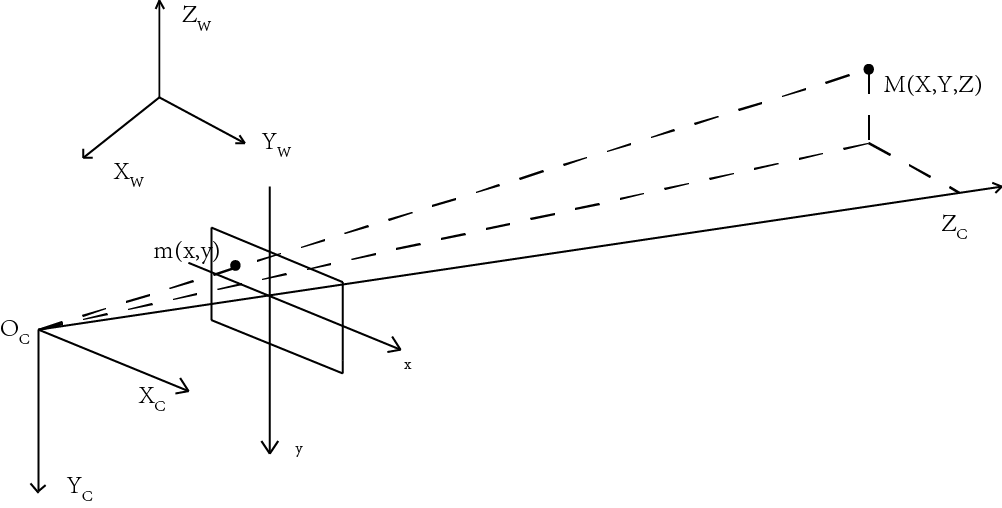
一般计算机视觉中都会假设摄像机的模型为针孔模型，针孔模型即为三维世界中的物体通过一个针孔投影在成像平面上，根据几何成像关系能够得出：像平面距离光心的距离，即为摄像机的焦距，摄像机的焦距将是之后我们求取的重要的参数。如下图所示。能够得出：在摄像机坐标系下空间中的一点M（X,Y,Z）投影到图像坐标系上的一点m（x，y）是满足相似关系的，这种相似关系是我们下面推导的基础。

---

1.2、相机标定

---

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。

无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

标定相机后通常是想做两件事：一个是由于每个镜头的畸变程度各不相同，通过相机标定可以校正这种镜头畸变矫正畸变，生成矫正后的图像；另一个是根据获得的图像重构三维场景。

---

1.3、相机参数

16个单目相机的参数：

10个内部参数（只与相机有关）

• 5个内部矩阵参数$K:f,dx,dy,u_0,v_0$（也可视作4参数$f_x,f_y,u_0,v_0$）。
• 5个畸变参数$D:k_1,k_2,k_3,p_1,p_2$。

6个外部参数（取决于相机在世界坐标系的位置）

• 3个旋转参数R
• 3个平移参数T

---

1.4、坐标系介绍

为了说明白，建议先介绍图像的坐标系，再逐步推广到世界坐标系，最后说明各个坐标系是如何变化的，从而给出相机的内参和外参。

---

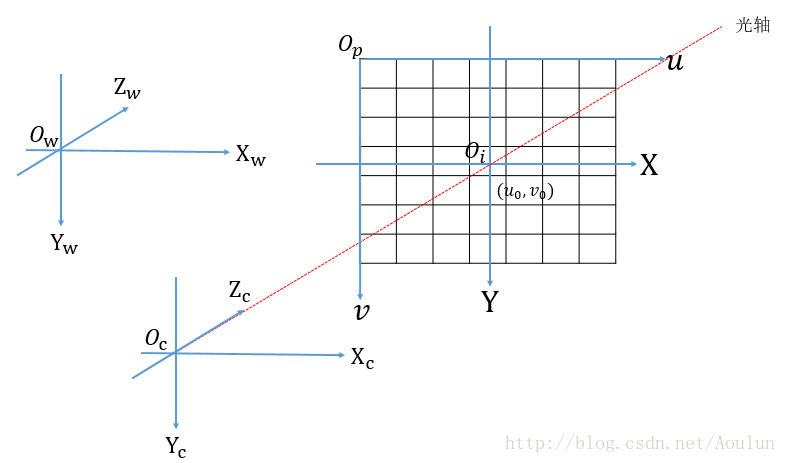
1.4.1、像素坐标系

像素坐标就是像素在图像中的位置。一般像素坐标系的左上角的顶点就是远点，水平向右是u轴，垂直向下是v轴。

例如，在上图中，任意一个像素点的坐标可以表示为$(u_i,v_i)$。

---

1.4.2、图像坐标系

在像素坐标系中，每个像素的坐标是用像素来表示的，然而，像素的表示方法却不能反应图像中物体的物理尺寸，因此，有必要将像素坐标转换为图像坐标。

将像素坐标系的原点平移到图像的中心，就定为图像坐标系的原点，图像坐标系的x轴与像素坐标系的u轴平行，方向相同，而图像坐标系的y轴与像素坐标系的v轴平行，方向相同。

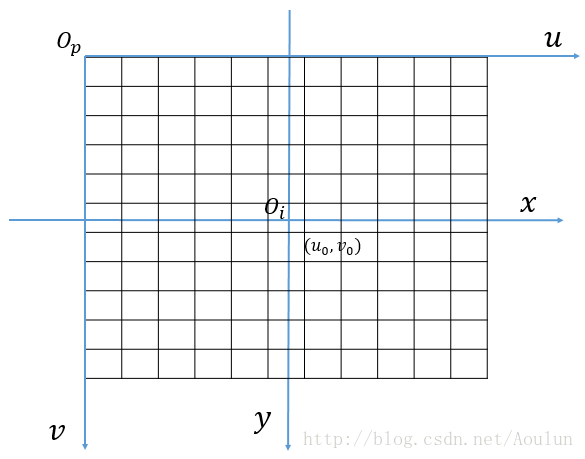
在图中，假设图像中心的像素坐标是$(u_0,v_0)$，相机中感光器件每个像素的物理尺寸是$dx * dy$，那么，图像坐标系的坐标$(x,y)$与像素坐标系的坐标$(u,v)$之间的关系可以表示为：

$$\begin{cases} x=udx-u_0dx \\[2ex] y=vdy-v_0dy \end{cases}$$

写成矩阵的形式就为：

$$\begin{bmatrix} x \\ y \\ \end{bmatrix}=\begin{bmatrix}dx & 0\\0 & dy\end{bmatrix}\begin{bmatrix} u\\ v \\ \end{bmatrix} +\begin{bmatrix} -u_0dx \\ -v0d_y \\ \end{bmatrix}$$

改写为齐次坐标的形式：

$$\begin{bmatrix} x \\ y \\1\\ \end{bmatrix}=\begin{bmatrix}dx & 0&0\\0 & dy&0\end{bmatrix}\begin{bmatrix} u\\ v \\0\\ \end{bmatrix} +\begin{bmatrix} -u_0dx \\ -v0d_y \\ \end{bmatrix}=\begin{bmatrix}dx & 0&-u_0dx\\0 & dy&-v_0dy\\0&0&1\end{bmatrix}\begin{bmatrix} u\\ v \\ 1\end{bmatrix}$$

---

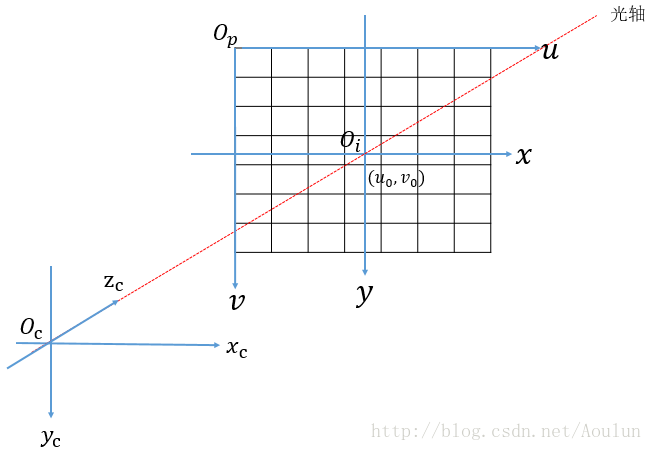
1.4.3、相机坐标系

相机坐标系是以相机的光轴作为Z轴，光线在相机光学系统的中心位置就是原点$O_c$（实际上就是透镜的中心）,相机坐标系的水平轴$X_c$与垂直轴$Y_c$分别与图像坐标系的$X$轴和$Y$轴平行。在图中，相机坐标系的原点与图像坐标系的原点之间的距离$O_cO_i$之间的距离为$f$(也就是焦距)。

上图中，如果有一个物体成像到图像坐标系，则可以用下图来表示（B点是相机坐标系中物体的点坐标，P是图像坐标系中成像的坐标）：

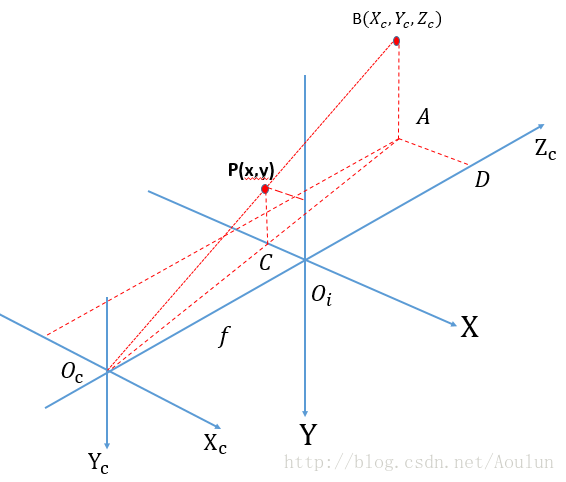
可以知道相机坐标系与图像坐标系的关系为：

$$\frac{O_cO_i}{O_cD}=\frac{O_i}{DA}=\frac{PC}{BA}=\frac{O_cC}{O_cA}\implies\frac{f}{Z_c}=\frac{x}{X_c}=\frac{y}{Y_c}\implies X_c=\frac{xZ_c}{f}\implies Y_c=\frac{yZ_c}{f}$$
$$\implies \begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix}=\begin{bmatrix}\frac{z_c}{f}&0&0\\0&\frac{z_c}{f}&0\\0&0&Z_c\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}$$

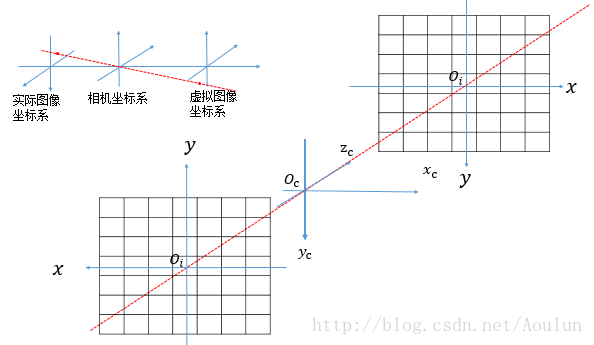
好了，那么为什么$O_cO_i$这个距离是焦距呢？下面做一些推导。大部分的文章在介绍这一点的时候，也有欠缺，为什么像素坐标系会在相机坐标系的前面呢，按道理说，相机坐标系是以相机的透镜中心为原点，那像素坐标系和图像坐标系为什么不在后面呢？这里做一个说明。

（1）本文的第一个图就是小孔成像的原理图。像平面就是成像的位置，这个是用户自己设定的，就是CCD传感器的位置，而焦平面就是镜头的焦距所在平面。当像平面刚好和焦平面重合时，此时所成的像是最清晰的。所以，这也就是为什么上面的公式中相机坐标系的原点到图像坐标系的原点的距离就是焦距。（实际上，由于物理条件的限制，像平面和焦平面是不可能完全重合的。）

（2）同样是本文的第一个图，我们可以看到像平面在光学系统的右面，而在推导相机标定的坐标系关系时，却认为光线先通过成像平面，再在相机坐标系上汇聚到一个点，实际上，如果用下图来说明，可能就更清楚一点。就是推导的时候，把像平面用虚拟像平面代替了。

---

1.4.4、世界坐标系

世界坐标系是图像与真实物体之间的一个映射关系。如果是单目视觉的话，主要就是真实物体尺寸与图像尺寸的映射关系。如果是多目视觉的话，那么就需要知道多个相机之间的关系，这个关系就需要在同一个坐标系下进行换算。在下图中，世界坐标系的原点是$O_w$,而$X_w,Y_w,Z_w$轴并不是与其他坐标系平行的，而是有一定的角度，并且有一定的平移。

当对相机坐标系安装一定的参数，分别绕着$X，Y，Z$轴做平移和旋转后，就得到在世界坐标系中的坐标。
平移表示：

$$\begin{cases} X_w=X_c+t_x \\[2ex]Y_w=Yc+t_y\\[2ex]Z_w=Z_c+t_z \end{cases}$$

而对于旋转，可以采用如下的方法，给定一个基本旋转矩阵和基本矩阵

$$R=\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta \end{bmatrix}$$

$$\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$$

对于三坐标轴旋转，当绕着X轴旋转时，保持基本矩阵的第1列不变，有如下的旋转矩阵：

$$\begin{bmatrix}X_w&Y_w&Z_w&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&cos\alpha&sin\alpha&0\\0&-sin\alpha&cos\alpha&0\\0&0&0&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}R_x$$

当绕着Y轴旋转时，保持基本矩阵的第2列不变，有如下的旋转矩阵：

$$\begin{bmatrix}Z_w&Y_w&X_w&1\end{bmatrix}=\begin{bmatrix}Z_c&Y_c&X_c&1\end{bmatrix}\begin{bmatrix}cos\beta&0&sin\beta&0\\0&1&0&0\\-sin\beta&0&cos\beta&0\\0&0&0&1\end{bmatrix}$$ $$\implies\begin{bmatrix}X_w&Y_w&Z_w&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}\begin{bmatrix}cos\beta&0&-sin\beta&0\\0&1&0&0\\sin\beta&0&cos\beta&0\\0&0&0&1\end{bmatrix}$$ $$=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}R_y$$

当绕着Z轴旋转时，保持基本矩阵的第3列不变，有如下的旋转矩阵

$$\begin{bmatrix}X_w&Y_w&Z_w&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}\begin{bmatrix}cos\gamma&sin\gamma&0&0\\-sin\gamma&cos\gamma&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}R_z$$

那么，整个相机坐标系到世界坐标系的变换公式为

$$\begin{bmatrix}X_w&Y_w&Z_w&1\end{bmatrix}=\begin{bmatrix}X_c&Y_c&Z_c&1\end{bmatrix}\begin{bmatrix}R&0\\T&1\end{bmatrix}$$
$$R=R_xR_yR_z$$
$$T=\begin{bmatrix}t_x&t_y&t_z\end{bmatrix}$$

---

1.5、相机的内参和外参

---

通过前面的几个步骤，我们已经得到了各个坐标系之间的相互转换关系，进一步的就可以得到从像素坐标系到世界坐标系的变换关系：

$$\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}=\color{red}{\begin{bmatrix}R&T \\0&1\end{bmatrix}}\color{blue}{\begin{bmatrix}\frac{Z_cdx}{f}&0&\frac{-Z_cu_0dx}{f}\\0&\frac{Z_cdy}{f}&\frac{-Z_cv_0dx}{f}\\0&0&Z_c\\0&0&1\end{bmatrix}}\begin{bmatrix}u\\v\\1\end{bmatrix}$$

公式中，红色的框就表示相机的外参，可以看到，外参就是相机相对于世界坐标系的旋转和平移变换关系。内参是相机固有的属性，实际上就是焦距，像元尺寸。同时还可以看到，公式中有一个$Z_c$，它表示物体离光学中心的距离。这也就说明，在标定的时候，如果物体在距离相机的不同位置，那么我们就必须在不同的位置对相机做标定。简单点来理解就是，当物体离相机远的时候，在图像上就很小，那么一个像素代表的实际尺寸就大，当物体离相机近的时候，那么成像效果就大，一个像素代表的实际物体尺寸就小。因此，对于每一个位置都需要去标定。

---

1.6、齐次坐标系

---

在介绍坐标系变换理论的时候，为什么要用齐次坐标呢？网上很多的文章在这一点上没有说明白，导致读者在看的时候糊里糊涂，莫名其妙。有的人就会问了，不就是为了使得表达的方便吗？那我只能说，太片面了啊，因为我之前在这里也有很多的困惑。所以在这里，我就按照自己的理解做一些推导。我相信，如果耐心的读者能够读到这里，希望我们都有一些启发，毕竟是我个人的理解，至于没有读到这里的，那就只能有缘再见了。

先说一说什么叫齐次坐标系：能够明显的区分点与向量，并且便于计算机做图形处理时进行仿射变换的坐标系。

在欧式空间，两条平行线是不会相交的（可以想象成两条平行的光线）。但是，再想象一下或者我们经常看到的例子，比如平行的火车轨道，如果我们站在火车轨道的正中间，向很远处观察两条轨道，是不是感觉两条轨道在很远处相交了，这就是透视空间。透视的英文单词是perspective，英文单词的解释是：the art of creating an effect of depth and distance in a picture by representing people and things that are far away as being smaller than those that are nearer the front。仔细的揣摩一下就类似于坐在那个地方画画，怎么表达轨道是无限往前走的呢，这就是一种透视的原理。

例如，在欧式空间，表示一个三维的点和一个三维的向量可以采用如下的方法：

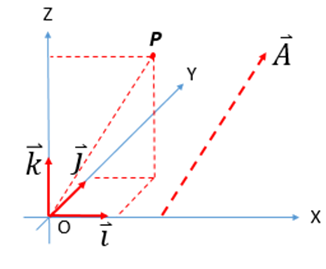
点坐标：

$$P=(x,y,z)$$ 向量： $$\overrightarrow{A}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$$

由于向量只有方向和大小，如何只给出（x,y,z）,无法知晓这到底是向量还是点。好了，如何来做呢。

$P$可以看做是一个点相对于原点的位移，那么

$$P-\overrightarrow{O}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\implies P=\overrightarrow{O}+x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$$

通过矩阵的变换

$$p=\begin{bmatrix}\overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}&\overrightarrow{o}\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}$$
$$A=\begin{bmatrix}\overrightarrow{i}&\overrightarrow{j}&\overrightarrow{k}&\overrightarrow{o}\end{bmatrix}\begin{bmatrix}x\\y\\z\\0\end{bmatrix}$$

可以看到，点和向量区分的方式是最后一个数值是否为1。

即：
(1) 从普通坐标系变换到齐次坐标系如果是点$(x,y,z)$则变换为$(x,y,z,1)$，如果是向量$(x,y,z)$则变换为$(x,y,z,0)$；
(2) 从齐次坐标系变换到普通坐标系如果是点$(x,y,z,1)$则变换为$(x,y,z)$，如果是向量$(x,y,z,0)$则变换为$(x,y,z)$。

---

1.7、相机模型小结

---

(1). 图像坐标系到素转化
由于相机的像素具有物理尺寸，设每个为由于相机的像素具有物理尺寸，设每个为$dx$和$dy$，则任意像 ，则任意像素在像素坐标系和图像坐标系的关系如下所示：

$$u=\frac{x}{dx}+u_0$$
$$v=\frac{y}{dy}+v0$$

写成矩阵形式为：

$$\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx}&0&u_0\\0&\frac{1}{dy}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}$$

其中$(x,y)$和$(u,v)$分别为物体的图像坐标和像素坐标，$(u_0,v_0)$为图像坐标系原点在像素坐标系下的摄像机光轴与平面相交处。理论位于图像中心。

(2). 相机坐标系到图像转化
设相机坐标系下物体为$(x_c,y_c,z_c)$，图像坐标为$x,y$.根据相似三角形原理可知：

$$x=\frac{f}{z_c}x_c$$
$$y=\frac{f}{z_c}y_c$$

写成矩阵形式为：

$$\begin{bmatrix}x\\y\\1\end{bmatrix}=\frac{1}{z_c}\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}$$

(3). 世界坐标系到相机转化
设世界坐标系下物体坐标为$(x_w,y_w,z_w)$，相机坐标系下坐标为$(x_c,y_c,z_c)$，二者具有线性转化关系。在齐次坐标系下二者可用下面等式转化：

$$\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}=\begin{bmatrix}R&t\\0&1\end{bmatrix}\begin{bmatrix}x_w\\y_w\\z_c\\1\end{bmatrix}$$

其中，$R$为3*3正交旋转矩阵，$t$为平移向量。

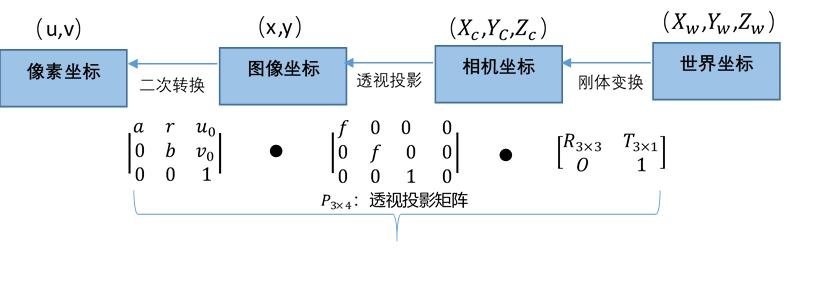
综上，坐标转化可写为

$$z_c\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx}&0&u_0\\0&\frac{1}{dy}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix}$$
$$=\begin{bmatrix}a_x&0&u_0&0\\0&a_y&v_0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}R&t\\0&1\end{bmatrix}\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix}$$
$$=KM\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix}$$

$$\begin{bmatrix}u\\v\\1\end{bmatrix}=\lambda KM\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix}=\lambda K\begin{bmatrix}r_1&r_2&r_3&t\end{bmatrix}\begin{bmatrix}x_w\\y_e\\z_w\\1\end{bmatrix}$$

当物体在世界坐标系下的$z_w$坐标为0时，上面的式子可简化为：

$$\begin{bmatrix}u\\v\\1\end{bmatrix}=\lambda K\begin{bmatrix}r_1&r_2&r_3&t\end{bmatrix}\begin{bmatrix}x_w\\y_w\\0\\1\end{bmatrix}=\lambda K\begin{bmatrix}r_1&r_2&t\end{bmatrix}\begin{bmatrix}x_w\\y_w\\1\end{bmatrix}=H\begin{bmatrix}x_w\\y_w\\1\end{bmatrix}$$

由于矩阵$K$只由相机本身决定，所以称为相机内参矩阵，$M$为外参矩阵，H为单应性矩阵。由于计算的坐标系为齐次坐标系，所以$H$的自由度为8。

---

1.8、张正友标定法

张氏标定方法是张正友在 1998 年提出的基于一个平面的棋盘格标定的方法。

简单的介绍一下张氏标定算法的主要流程：
1. 打印一张棋盘格，将其贴在一个平面上，作为参考平面。
2. 通过旋转、移动参考平面，利用摄像机拍取一组照片。
3. 从照片当中提取角点。
4. 估算在没有畸变的情况下的内参数和外参数。
5. 利用最小二乘算法计算径向畸变。
6. 利用极大释然估计，重新再修正所有的参数。

---

1.8.1、预备知识

从像素坐标系$(u,v)$到世界坐标系$(X_w,Y_w,Z_w)$

公式如下：

$$\frac{1}{Z_c}\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\frac{f}{S_x}&r&u_0\\0&\frac{f}{S_y}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}R_{3\times 3}&T_{3\times 1}\\O&1\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}=K_{3\times 3}\begin{bmatrix}R_{3\times 3}&T_{3\times 1}\\O&1\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}$$

$$s\begin{bmatrix}u\\v\\1\end{bmatrix}=P_{3\times 4}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}$$

$K_{3\times 3}$：摄像机内参矩阵（含5个内参）
$P_{3\times 4}$：透视投影矩阵
$s=\frac{1}{Z_c}$：未知的尺度因子

为了和张正友教授的论文(A flexible new technique for camera calibration Z. Zhang) 相统一，现在把公式符号统一一下。

$$s\begin{bmatrix}u\\v\\1\end{bmatrix}=P_{3\times 4}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}\implies s\begin{bmatrix}u\\v\\1\end{bmatrix}=A\begin{bmatrix}R_{3\times 3}&t_{3\times 1}\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}$$

令$\tilde{m}=[u,v,1]^T,\tilde{M}=[X,Y,Z,1]^T,s\tilde{m}=A\begin{bmatrix}R &t\end{bmatrix}\tilde{M}$,
且$K_{3\times 3}\implies A=\begin{bmatrix}\alpha&\gamma&u_0\\0&\beta&v_0\\0&0&1\end{bmatrix},R_{3\times 3}=\begin{bmatrix}r_1&r_2&r_3\end{bmatrix}$

在推导中，需有以下数学基础：

• 第一点：旋转向量$R$为正交矩阵，所以有以下的性质：
  
  • $r_1^{T}r_2=0$
  • $r_1^{T}r_1=r_2^{T}r_2=1$
• 第二点：$s$是尺度因子，它的出现只是为了方便运算，而且对于齐次坐标，尺度因子不会改变坐标值 。

---

1.8.2、公式推导

(1)、标定平面到图像平面的单应性(Homography)

因为张氏标定是一种基于平面棋盘格的标定，所以想要搞懂张氏标定，首先应该从两个平面的单应性(Homography)映射开始着手。
单应性(Homography) ： 在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先看一下，图像平面与标定物棋盘格平面的单应性.

因为标定物是平面，所以我们可以把世界坐标系构造在 Z = 0 的平面上。然后进行单应性计算。令 Z = 0 可以将上式转换为如下形式：

$$s\begin{bmatrix}u\\v\\1\end{bmatrix}=A\begin{bmatrix}r_1&r_2&r_3&t\end{bmatrix}\begin{bmatrix}X\\Y\\0\\1\end{bmatrix}=A\begin{bmatrix}r_1&r_2&t\end{bmatrix}\begin{bmatrix}X\\Y\\1\end{bmatrix}$$

$$s\tilde{m}=H\tilde{M},H=A\begin{bmatrix}r_1&r_2&t\end{bmatrix}$$

H就是单应性矩阵，即

$$s\begin{bmatrix}u\\v\\1\end{bmatrix}=H\begin{bmatrix}X\\Y\\1\end{bmatrix},令H=\begin{bmatrix}h_1&h_2&h_3\end{bmatrix}$$

H 是一个$3\times 3$的矩阵，并且有一个元素作为齐次坐标。因此，H有8个未知量待解（可以分析一下，A 有5个未知量，后面的$[r_1,r_2,t]$有三个未知量，一共8个）。

$(X,Y)$作为标定物的坐标，可以由设计者人为控制，是已知量 。$(u,v)$ 是像素坐标，我们可以直接通过摄像机获得。一组对应的 $(X,Y) - (u,v)$ 我们可以获得两组方程。

现在有8个未知量待求，所以至少要8个方程。所以至少需要4组对应的点。所以有4组$(X,Y) - (u,v)$就可以算出，图像平面到世界平面的 单应性矩阵H，这也是张正友标定采用四个角点的棋盘作为标定物的一个原因（笔者推测）。

(2)、利用约束条件求解内参矩阵$A$
由(1)可知，应用4个点我们可以获得单应性矩阵H。但是H是内参矩阵和外参矩阵的合体。我们想要最终分别获得内参和外参。所以需要想个办法，先把内参求出来。然后外参也就随之解出来了。

$$\begin{bmatrix}h_1&h_2&h_3\end{bmatrix}=\lambda A\begin{bmatrix}r_1&r_2&t\end{bmatrix}$$

其中，$\lambda$是任意的标量。由所学知识(正交矩阵的性质)且$r_1$和$r_2$是正交的可知

$$h_1^TA^{-T}A^{-1}h_2=0$$
$$h_1^TA^{-T}A^{-1}h_1=h_2^tA{-T}A^{-1}h_2$$

上式中的$h_1,h_2$是通过求解单应性矩阵$H$ 求出来的，所以未知量只剩下内参矩阵$A$。$A$中含有5个参数，如果需要完全解出来这5个未知量，则需要3个不同的单应性矩阵H（因为3个不同的单应性矩阵$H$在2个约束条件下可以产生6个方程），那么如何得到3个不同的单应性矩阵$H$呢？那就是3张不同的标定平面的照片，我们大多是通过改变摄像机与标定板间的相对位置来获得不同的标定照片（如果用2张照片进行标定，就要舍去一个内参 r=0）。

当然这只是张正友标定法不断变换标定板方位的 第一个原因 。第二个原因 是张正友提到的 最大似然估计 。

令

$$B=A^{-T}A^{-1}\equiv\begin{bmatrix}B_{11}&B_{12}&B_{13}\\B_{21}&B_{22}&B_{23}\\B_{31}&B_{32}&B_{33}\end{bmatrix}$$
$$=\begin{bmatrix}\frac{1}{\alpha^2}&-\frac{\gamma}{\alpha^2\beta}&\frac{v_0\gamma-u_0\beta}{\alpha^2\beta}\\-\frac{\gamma}{\alpha^2\beta}&\frac{\gamma^2}{\alpha^2\beta^2}+\frac{1}{\beta^2}&-\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2}\\\frac{v_0\gamma-u_0\beta}{\alpha^2\beta}&-\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2}&\frac{(v_0\gamma-u_0\beta)^2}{\alpha^2\beta^2}+\frac{v_0^2}{\beta^2}+1\end{bmatrix}$$

可以看出 矩阵$B$是一个对称矩阵，有效的元素只有6个，所以定义一个6维的向量

$$b=[B_{11},B_{12},B_{13},B_{22},B_{23},B_{33}]^T$$

假设$H$的第$i$列向量为$h_i=[h_{i1},h_{i2},h_{i3}]^T$，然后我们可以得到

$$h_1^T=Bh_j=v_{ij}^Tb$$
式中$v_{ij}=[h_{i1}h_{j1},h_{i1}h_{j2}+h_{i2}h{j1},h_{i2}h_{j2},h_{i3}h_{j1}+h_{i1}h_{j3},h_{i3}h_{j2}+h_{i2}h_{j3},h_{i3}h_{j3}]^T$,于是，两个基本约束式可以写为齐次式
$$\begin{bmatrix}v_{12}^T\\(v_{11}-v_{22})^T\end{bmatrix}$$

如果观测了n张图片，迭代可以得到

$$Vb=0$$

式中$V$是一个$2n\times 6$矩阵。若$n \geq 3$,通常会得到一个唯一解$b$。若$n=2$，令倾斜约束参数$\gamma=0$，即$[0,1,0,0,0,0]b=0$,这作为额外的方程代入上面的等式中，得到的解是被熟知的与最小奇异解相关的特征向量$V^TV$.

一旦$b$被解出来，就可以计算内参矩阵$A$。

$$B=\lambda A^{-T}A$$
$$v_0=\frac{B_{12}B_{13}-B_{11}B_{23}}{B_{11}B_{22}-B_{33}^2}$$
$$\lambda=B_33-\frac{[B_{33}+v_0(B_{12}B_{13}-B_{11}B_{23})]}{B_{11}}$$
$$\alpha=\sqrt\frac{\lambda}{B_{11}}$$
$$\beta=\sqrt{\frac{\lambda B_{11}}{(B_{11}B_{12}-B_{12}^2)}}$$
$$\gamma=-\frac{B_{12}\alpha^2}{\lambda}$$
$$v_0=\gamma\frac{ v_0}{\alpha}-B_{13}\frac{\alpha^2}{\lambda}$$

一旦$A$已知，就可以求解出外参矩阵：
由

$$\begin{bmatrix}h_1&h_2&h_3\end{bmatrix}=\lambda A\begin{bmatrix}r_1&r_2&r_3\end{bmatrix}$$

得

$$\begin{cases}r_1=\lambda A^{-1}h_1\\[2ex]r_2=\lambda A^{-1}h_2\\[2ex]r_3=r_1\times r_2\\[2ex]t=\lambda A^{-1}h_3\end{cases},\lambda=\frac{1}{||A^{-1}h_1||}=\frac{1}{||A^{-1}{h_2}||}$$

---

1.9、张正友标定法小结

---

相机标定 分为两步，第一步通过同幅图片中的对应点计算单性矩阵，第一步通过同幅图片中的对应点计算单性矩阵，二步利用不同图片提供的约束求解内参和外数。这里我们令$Z_w=0$。

(1)单应性矩阵计算

$$H=\lambda K\begin{bmatrix}r_1&r_2&t\end{bmatrix}=\begin{bmatrix}h_1&h_2&h_3\end{bmatrix}=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix}$$

由于$H$的自由度为8，所以我们可以令$h_{33}=1$，根据世界坐标系与像素坐标系的关系：

$$\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&1\end{bmatrix}\begin{bmatrix}x_w\\y_w\\1\end{bmatrix}$$

我们可以得到两个方程：

$$\begin{cases}h_{31}x_wu+h_{32}y_wu+u=h_{11}y_w+h_{12}y_w+h_{13}\\[2ex]h_{31}x_wv+h_{32}y_wv+v=h_{21}x_w+h_{22}y_w+h_{23}\end{cases}$$

将其写为矩阵形式：

$$\begin{bmatrix}x_w&y_w&1&0&0&0&-ux_w&-uy_w&-u\\0&0&0&x_w&y_w&1&-vx_w&-vy_w&-v\end{bmatrix}\begin{bmatrix}h_{11}\\h_{12}\\h_{13}\\h_{21}\\h_{22}\\h_{23}\\h_{31}\\h_{32}\\1\end{bmatrix}=Sh=0$$

该方程的未知参数有8个，因此确定4个点的世界坐标与像素对应关系即可求解该方程。我们通常取同一张图片的多个点求该方程的最小二乘解，解得的$h$为$S^TS$的最小特征值对应的特征向量 。

(2)内外参数计算
上面的方法计算的单应性矩阵与真实单应性矩阵可能相差一个比例因子。即：

$$\begin{bmatrix}h_1&h_2&h_3\end{bmatrix}=\lambda K\begin{bmatrix}r_1&r_2&r_3\end{bmatrix}$$

由于$r_1$和$r_2$为正交的单位向量，因此得到两个约束$r_1^Tr_2=0$,$||r_1||=||r_2||=1$。

又因为$r_1=\frac{1}{\lambda}K^{-1}h_1,r_2=\frac{1}{\lambda}K^{-1}h_2$，故：

$$h_1^TK^{-T}K^{-1}h_2=0$$
$$h_1^TK^{-T}K^{-1}h_1=h_2^TK^{-T}K^{-1}h_2$$

令$B=K^{-T}K^{-1}$，$B$为对称矩阵。其中：

$$K=\begin{bmatrix}\alpha_x&\gamma&u_0\\0&a_y&v_0\\0&0&1\end{bmatrix},K^{-1}=\begin{bmatrix}\frac{1}{a_x}&-\frac{\gamma}{a_xa_y}&\frac{\gamma v_0-a_yu_0}{a_xa_y}\\0&\frac{1}{a_y}&-\frac{v_0}{a_y}\\0&0&1\end{bmatrix}$$

$$K^{-T}K^{-1}=\begin{bmatrix}\frac{1}{a_x}&0&0\\-\frac{\gamma}{a_xa_y}&\frac{1}{a_y}&0\\\frac{\gamma v_0-a_yu_0}{a_xa_y}&-\frac{v_0}{a_y}&1\end{bmatrix}\begin{bmatrix}\frac{1}{a_x}&-\frac{\gamma}{a_xa_y}&\frac{\gamma v_0-a_yu_0}{a_xa_y}\\0&\frac{1}{a_y}&-\frac{v_0}{a_y}\\0&0&1\end{bmatrix}$$
$$=\begin{bmatrix}\frac{1}{a_x^2}&-\frac{\gamma}{a_x^2a_y}&\frac{\gamma v_0-a_yu_0}{a_x^2a_y}\\-\frac{\gamma}{a_x^2a_y}&\frac{\gamma^2}{a_x^2a_y^2}+\frac{1}{a_y^2}&-\frac{\gamma(\gamma v_0-a_yu_0)}{a_x^2a_y^2}-\frac{v_0}{a_y^2}\\\frac{\gamma v_0-a_yu_0}{a_x^2a_y}&-\frac{\gamma(\gamma v_0-a_yu_0)}{a_x^2a_y^2}-\frac{v_0}{a_y^2}&\frac{(\gamma v_0-a_yu_0)^2}{a_x^2a_y^2}+\frac{v_0^2}{a_y^2}+1\end{bmatrix}$$

上面的$K^{-T}K^{-1}$由于是对称矩阵，因此共有6个未知矩阵元素，这6个未知量由内参的5个子参数构成。

令：

$$b=\begin{bmatrix}B_{11}&B_{12}&B_{22}&B_{13}&B_{23}&B_{33}\end{bmatrix}^T$$
$$v_{ij}=\begin{bmatrix}h_{i1}h_{j1}&h_{i1}h_{j2}+h_{i2}h_{j1}&h_{i1}h_{j3}+h{i3}h_{j1}&h_{i2}h_{j3}+h_{i3}h_{j2}&h_{i3}h_{j3}\end{bmatrix}^T$$

则有：

$$\begin{cases}h_1^TK^{-T}K_{-1}h_2=0\\[2ex]h_1^TK^{-T}K^{-1}h_1=h_2^TK^{-T}K^{-1}h_2\end{cases}\iff\begin{bmatrix}v_{12}^T\\(v_{11}-v_{22})^T\end{bmatrix}b=0$$

每张图片的单应性矩阵可以提供两个方程，3张图片即可解出所有的$B$参数，从而解出内参。

当内参矩$K$和单应性矩$H$均已知后，外参由下面方程求得：

$$r_1=\frac{1}{\lambda} K^{-1}h_1$$
$$r_2=\frac{1}{\lambda} K^{-1}h_2$$
$$t=\frac{1}{\lambda} K^{-1}h_3$$
$$r_3=r_1\times r_2$$
$$||r_1||=||r_2||=1$$

通过张氏标定，我们并不能得到：焦距(f)和像素的物理尺寸$(S_x,S_y)$两个参数。因为我们在求解内参阵A时，求解出的是α和β($\alpha=\frac{f}{S_x},\beta= \frac{f}{S_y}$,分别代表焦距长度上，x轴和y轴像素的个数)。

虽然，没有求得焦距，但这并不影响，我们在三维坐标恢复时，进行三角运算。因为彼时，我们的计算中用到的也是α和β。

---

1.10、双目相机标定

---

对于双目立体视觉，我们有两个摄像头。它们就像人的一双眼睛一样，从不同的方向看世界。两只眼睛中的图像的视差，让我们对世界有了三维的认识。

那么，想要知道视差，首先应该知道双目视觉系统中两个摄像头之间的相对位置关系。我们可以通过同时对两个摄像头进行标定，分别得到二者相对同一坐标系的旋转矩阵和平移矩阵。获得这两个矩阵的过程，就是立体标定的过程。也即是：从张氏标定走向立体标定！

双目视觉中不仅需要标定两个相机各自的参数，还需要标定两个摄像机之间的旋转平移关系。设两个摄像机外参和矩阵分别为$R_1,T_1,R_2,T_2$，三维空间中一点P的世界坐标为$P_w$，该点在两个相机的世界坐标分别为$P_1,P_2$，则有：

$$\begin{cases}P_1=R_1P_w+T_1\\[2ex]P_2=R_2P_w+T_2\end{cases}$$

两个方程消去$P_w$

$$P_2=R_2R_1^{-1}(P_1-T_1)+T_2=R_2R_1^{-1}P_1+T_2-R_2R_1^{-1}T_1$$

设由第一个摄像机转化到第二个摄像机的旋转和平移矩阵分别为$R,T$，则

$$\begin{cases}R=R_2R_1^{-1}\\[2ex]T=T_2-R_2R_1^{-1}T_1\end{cases}$$

---

1.11、标定投影仪

---

将传统的双目视觉系统中的一个摄像机替换成投影仪主要是为了解决双目视觉当中比较难以解决的对应点匹配问题

由于投影仪只是一个信息的发射设备，不具备接受信息的能力。所以投影仪的标定过程一般都需要借助结构光系统当中的摄像机来完成。在多数情况下，一般都将投影仪当成了一个逆光路的摄像机。那么利用就可以对投影仪采用和摄像机相同的非线性畸变的数学模型。

三维重建系统是利用摄像机采集的二维图像来获取物体的三维信息，摄像机摄取的二维图像上的每一点都有空间物体表面上的某一点与其对应，摄像机和投影仪模型就是来确定这些对应点之间的位置关系。

针孔模型是最简单的摄像机模型，这个模型也是目前应用最广泛的。其原理类似于小孔成像原理，摄像机针孔模型如图所示。

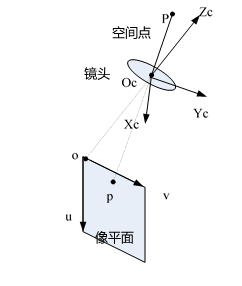
$Oc$ 是摄像机坐标系原点，即摄像机光心，$P( x_c, y_c, z_c)$是空间中的一点，$p (x_u , y_u )$ 是点$P( x_c,y_c,z_c)$透过摄像机透镜中心后在像平面上形成的一点。

摄像机和投影仪模型如图下所示，以 $Oc$为坐标原点，光轴方向为 $Z_c$ 轴建立的摄像机坐标系，$P$ 为空间中某一点，$P_c$ 点为点 $P$ 在摄像机相片中的像点，摄像机的相片中的像点一定有一个空间点与之对应。

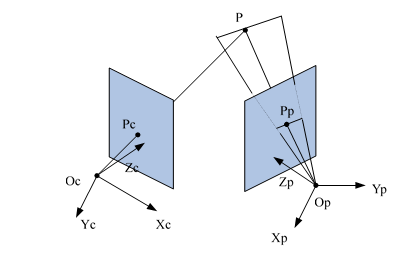
投影仪模型可以认为是一个反向的摄像机模型，摄像机模型是光穿过摄像机在相片上形成像点，投影仪模型则是投影仪发出的光穿过投影仪相片投射至空间。

在获得摄像机的参数后，同样需要对投影仪进行相似的标定，投影仪标定与摄像机标定方法是一致的，也是利用空间点坐标与图像像素坐标的相应位置关系，获得投影仪的内外部参数，从而得到整个系统的标定参数。

对投影仪的标定是通过使其投射标准图像来完成的，标准图像包含已知图像像素坐标的标识点。在投影仪标定中，通过已知标识点的图像像素坐标就可以得到其空间世界坐标，再由该点在世界坐标系与投影仪图像像素坐标系的坐标的变换关系，就能得到投影仪的内外部参数。

投影仪的标定原理如图所示，可以直观的看到校正板上的四个标识点 $A、B、C、D$ 组成一个矩形。$Oc$ 为摄像机光心，$Op$ 为投影仪光心。

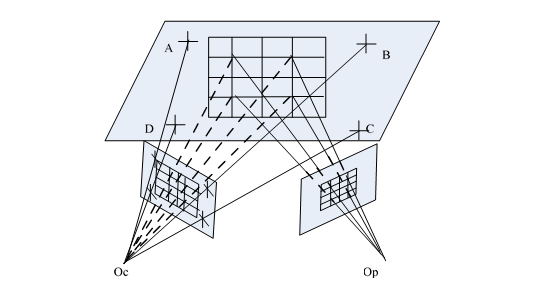
利用投影仪将投影图案投射到标定平面上，使用摄像机对其拍摄，投影仪标定平面如图所示。

摄像机标定是在已知某平面上的点的世界坐标的前提下，根据摄像机摄取的不同位置的图像来获取每幅图像的旋转矩阵 R 和平移矩阵T。为实现摄像机标定，利用四个标识点获取标定平面的 $R$ 和 $T$ 矩阵，进而得到校正平面的方程。同时，投影的图像点在摄像机的图像素坐标通过选取的投影图像点获得，接着根据得到摄像机中心 $Oc$ 到投影图像点的直线方程，结合校正平面方程就能得到投影的图像点在世界坐标系的坐标进而得到摄像机的标定参数。

投影仪投射的标准图案如图所示，投影仪将其投射到校正板上，利用摄像机摄取到的如图所示的投影平面，只需找到投影图案中的标识点就可以得到投影点的图像像素坐标。

令校正平面的旋转矩阵$R=\begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix}$，，平移矩阵$T=\begin{bmatrix}t_1\\t_2\\t_3\end{bmatrix}$，由$R$计算所得到的图像的平面法向量$n=\begin{bmatrix}r_{13}&r_{23}&r_{33}\end{bmatrix}^T$，设摄像机的平面原点的坐标为$o=\begin{bmatrix}t_{1}&t_{2}&t_{3}\end{bmatrix}^T$,从而计算得到平面点所在平面的方程为：

$$ax+by+cz+d=0$$

因此，我们可以通过得到的透过摄像机光心的各投影点的射线$L=\begin{bmatrix}l_{x}&l_{y}&l_{z}\end{bmatrix}^T$，结合坐标系变换关系有

$$s\begin{bmatrix}u\\v\\1\end{bmatrix}=H\begin{bmatrix}l_{x}\\l_{y}\\l_{z}\\1\end{bmatrix}$$

$$\begin{bmatrix}l_{x}\\l_{y}\\l_{z}\\1\end{bmatrix}=H^{-1}\begin{bmatrix}su\\sv\\s1\end{bmatrix}$$

其中，$H$为变换矩阵。结合上式与平面方程可以得到

$$al_x+bl_y+cl_z+d=0$$

由上式可以看出，通过求解方程，求出$s$就能得到投影点的坐标，然后再结合其图像坐标和空间坐标的相应的关系就得到投影仪标定的结果。

---

2、结构光编码

---

编码结构光三维重构测量技术是一种主动式三角测量技术，该技术以激光三角测量原理为理论基础，并融合了计算机测量技术、数字图像处理技术和相机标定技术等多种技术。编码结构光三维重构测量系统主要由工业摄像机、投影仪和计算机组成，其基本原理是：由投影仪将结构光编码图案投影到被测物体的表面，然后摄像机在另外一个角度对结构光图像进行同步拍摄，再将捕获的结构光图像输入计算机，进行解码处理，最后再根据系统标定的结果来计算特征点的三维坐标，从而完成被测物体表面的三维重构。

编码结构光三维重构技术主要由图像获取、结构光编码、结构光解码、系统标定和三维坐标计算等5个关键技术组成。

---

2.1、点云

---

三维图像是一种特殊的信息表达形式，其特征是表达的空间中三个维度的数据，表现形式包括：深度图（以灰度表达物体与相机的距离），几何模型（由CAD软件建立），点云模型（所有逆向工程设备都将物体采样成点云）。和二维图像相比，三维图像借助第三个维度的信息，可以实现天然的物体——背景解耦。点云数据是最为常见也是最基础的三维模型。点云模型往往由测量直接得到，每个点对应一个测量点，未经过其他处理手段，故包含了最大的信息量。这些信息隐藏在点云中需要以其他提取手段将其萃取出来，提取点云中信息的过程则为三维图像处理。

点云是在同一空间参考系下表达目标空间分布和目标表面特性的海量点集合，在获取物体表面每个采样点的空间坐标后，得到的是点的集合，称之为“点云”（Point Cloud）。

根据激光测量原理得到的点云，包括三维坐标（XYZ）和激光反射强度（Intensity），强度信息与目标的表面材质、粗糙度、入射角方向，以及仪器的发射能量，激光波长有关。
根据摄影测量原理得到的点云，包括三维坐标（XYZ）和颜色信息（RGB）。
结合激光测量和摄影测量原理得到点云，包括三维坐标（XYZ）、激光反射强度（Intensity）和颜色信息（RGB）。

---

2.2、编码结构光

---

主要的编码方法有时序编码、直接编码和空间编码三种。

时间编码优点是空间分辨率和测量精度高，但重构速度慢，不适合动态物体三维重构；直接编码理论上分辨率也比较高，但是解码相当困难，重构的精度也不高；空间编码只需投影一幅编码图像，重构速度快，适合动态测量，所以成为近年研究的热点。

---

2.3、时间编码

---

时序编码方法是按时间的先后顺序，将多张不同的编码图案投影到被测物体表面，该方法的优点在于多次投影使其具有重构精度较高的优点，但每次三维坐标的计算都需要多幅图像，所以不能对高速运动物体进行瞬时三维重构，通常也只能结合运动补偿的方法对低速运动物体进行局部表面三维重构，重构效率较低。在时序编码的发展过程中，其编码技术主要有以下几类：二值编码、n-ary编码、相位编码和混合编码等。

根据结构光测量原理知能否精确地确定扫描角$\alpha$ 是整个测量系统的关键，点结构光和线结构光系统是通过转镜等机械装置计算和确定扫描角，而图像编码及解码的意义就在于确定编码结构光即面结构光系统的扫描角。以两灰度级三位二进制时间编码简要说明时间编码的编码及解码原理。应用投射器向被测景物连续投射，如图所示的三幅图案，三幅图案中分别用亮暗两灰度将投射空间分为 8 个区域，显然每个区域对应各自的投射角，其中亮区域对应编码“1”，暗区域对应编码“0”。将投射空间中景物上一点在三幅编码图案中的编码值按投射次序组合，得到该点的区域编码值，由此确定该点所在区域进而解码获得该点的扫描角。

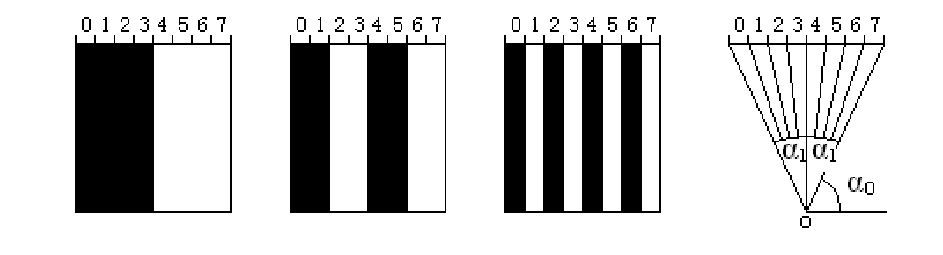
例如被测景物上一点 P处于第四区域内，在三幅图案中的编码值分别是 “0”、“1”、“1”，则该点的区域编码值为“011”，将二进制编码“011”转化为十进制编码，得到该点对应的区域序号为 k=3，其中 K的取值范围是 0 至 7 的整数。假设$\alpha_0$和$\alpha_1$已经被标定，其值是确定的常数，由于采用等宽条纹图案进行编码，根据几何关系，则点P 所在位置的扫描角可由下列公式确定：

$$\alpha =\alpha_0+arctan \begin{bmatrix}(2^{n-1}-k)\times \frac{tan\alpha_1}{2^{n-1}}\end{bmatrix}$$

其中 n 为强度图像总数，将$\alpha$代入系统的数学模型公式即可得到点 P 的三维坐标。

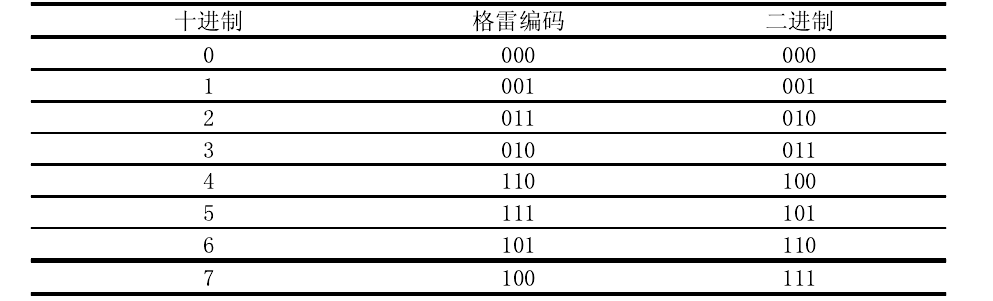
目前，在结构光测量中时间编码主要采用二进制编码(Binary Encoding)和格雷(Gray)编码两种。
如图所示，是投射的二进制编码，以投射三幅二进制编码图案为例，三幅图案的最小条纹周期依次减半，条纹图案投射到物体表面将其分成8个区域，每个区域代表一个周期。其中，黑色条纹二进制码值记为0；白色条纹二进制码值记为1，则可由一个三位二进制编码表示，获得1/8的分辨率。这样在每次投射中,图像的每个像素就可以获得一个唯一的二进制数“0”或“1”，待投射图案全部完成后，将像素所获得二进制数顺序组合起来,具有相同编码的像素构成了一个窄的带状区域,这样被测物空间就相应被分割成众多由二进制编码唯一确定的窄带状区域，最终三维图像的转换精度取决于条纹图案投射的密度。如图中P点，其在三幅投射图案中条纹分别是“黑”、“白”、“黑”，因此，其二进制编码为010。

通过对二进制编码图案进行观察，我们可以发现，如果某一点在第一幅编码图案的图像中处于黑白交界处，那么在接下来的编码图案投射图中也必然处于黑白交界的地方，例如，当十进制数由“3”变为“4”时，采用二进制码，则其编码将由“011”变为“100”，此时，三位二进制状态都发生变化，虽然我们看到的是同时转变，但从硬件的角度来看，设备的每一位状态并不是同时发生改变的，如第一位先转变成1，则数字暂时成为111，虽然很快第二位和第三位就会变成0，但是111这个暂时的状态很有可能会造成控制系统的不稳定。也就是说，尽管最终的结果是从3变到4，但出现了错误的中间转换过程。若不采用其他措施禁止这些中间错误结果输出，则将使设备产生较大的误差。因此其码值可能多位被误判，若误判存在于高位则解码误差较大。这样会大大增加计算机产生误判而导致解码错误的概率，为了解决这这一问题减少解码过程中的累计误差，格雷编码被引入时间编码方法中。

若采用格雷码，就不会产生这种较大的误差。因为当十进制数由“3”变为“4”时，其对应的格雷码将从“010”变为“110”，只有一位二进制数发生改变，也就无中间暂态出现，如表所示。因此，格雷编码相比二进制编码更为可靠。

下面给出三幅格雷编码图案，以便和二进制编码图案相比较，如图所示。格雷编码图案把测量空间分成8个区域，如果某一点在其中一幅的编码图案中处于黑白交界处，那么在其它几幅编码图案中该点必然不处于黑白交界处，也就是说，在投射的几幅格雷编码图案中任意一点作为黑白变化边界的机会最多只有一次。而在二进制编码图案中，如果某一点在当前图案中处于黑白交界处，那么在后面投射的图案中必然也处于黑白交界处。因此，相对于二进制编码，格雷码编码在解码的时候，能够大大减少出现解码错误的机会。图中和二进制编码图案相同位置的p点，其对应的格雷编码为011。

值得注意的是：由于摄像机拍摄到的图像是灰度值在0到255之间的灰度图像，并不是理想的黑白二值图像。因此，需要根据判据进行二值化处理,然后再由计算机将所得到的条纹图案进行黑白二值化处理，将图像中白色条纹区域的像素标记为“1”，黑色条纹区域的像素标记为“0”。

从图中我们还可以看出除了第一幅编码图案以外，格雷编码图案和二进制编码图案都不相同，在这些不同的图案中，相同投射次序的格雷编码图案周期是二进位编码图案周期的两倍，这样在编码图案相同的情况下格雷编码图案的制作精度更高。而在相同的制作精度下，格雷编码图案数更多。由此可见，采用格雷编码不仅能降低解码的出错率还能降低投射图案的制造误差，提高投射图案条纹精度。

---

2.4、空间编码

---

空间编码法与时序编码、直接编码相比，优点在于可以该编码可以用于动态物体三维重构，它只需一幅图像按某种方式来进行编码，图案中每个特征点的码字根据其周围邻近特征点的颜色信息、强度信息或者几何特性信息得到，因此可在复杂环境下对运动物体三维重构。空间编码可以分为：非线性编码，DeBruijn序列编码和M-arrays编码等。

Debruijn序列

数学中存在这样一个序列，它充满魔力，在实际工程中也有一部分的应用。今天就打算分享一下这个序列，它在 Google S2 中是如何使用的以及它在图论中，其他领域中的应用。这个序列就是德布鲁因序列 De Bruijn。

一. 从一个魔术开始说起

有这样一个扑克牌魔术。魔术师手上拿着一叠牌，给5个人(这里的人数只能少于等于32，原因稍后会解释)分别检查扑克牌，查看扑克牌的花色和点数是否都是不同的，即没有相同的牌。

检查完扑克牌，没有重复的牌以后，就可以给这5个人洗牌了。让这5个人任意的抽一叠牌从上面放到下面，即切牌。5个人轮流切完牌，牌的顺序已经全部变化了。

接着开始抽牌。魔术师让最后一个切牌的人抽走这叠牌最上面的一张，依次给每个人抽走最上面的一张。这时候抽走了5张牌。魔术师会说，“我已经看透了你们的心思，你们手上的牌我都知道了”。然后魔术师会让拿黑色牌的人站起来(这一步很关键！)。然后魔术师会依次说出所有人手上的牌。最后每个人翻出自己的牌，全部命中。全场欢呼。

二. 魔术原理揭秘

在整个魔术中，有三个地方比较关键。第一个是参与的人数只能少于等于32。一副完整的扑克牌中，总共有54张牌，但是除去2张鬼牌(因为他们花色只有2种)，总共就52张牌。在上述魔术中，所有的牌都用二进制进行编码，要想任意说出任意连续的5张牌，那么必须这副牌具有全排列的特性。即枚举所有种组合，并且每个组合都唯一代表了一组排列。

如果窗口大小为5，5张连续的扑克牌。二进制编码 25 = 32 ，所以需要32张牌。如果窗口大小为6，6张连续的扑克牌，二进制编码 26 = 64，需要64张扑克牌。总共牌只有52张，所以不可能到64张。所以32个人是上限了 。

第二个关键的地方是，只有让拿黑色的牌的人或者拿红色的牌的人站出来，魔术师才能知道这5个人拿到的连续5张扑克牌究竟是什么。其实魔术师说“我已经知道你们所有人拿到的是什么牌”的时候，他并不知道每个人拿到的是什么牌。

扑克牌除了点数以外，还有4种花色。现在需要32张牌，就是1-8号牌，每号牌都有4种花色。花色用2位二进制编码，1-8用3位二进制编码。于是5位二进制正好可以表示一张扑克牌所有信息。

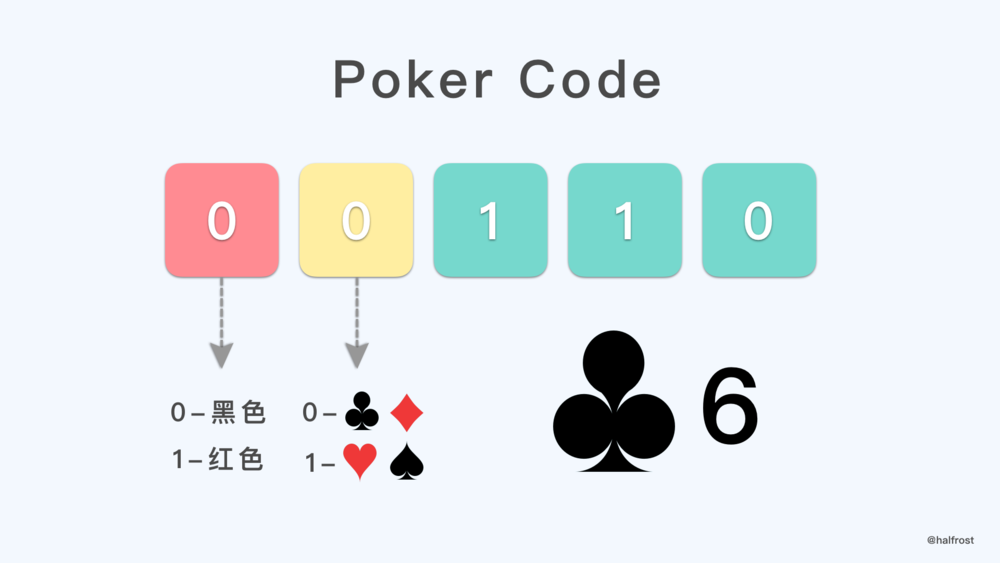
如上图，00110 表示的就是梅花6 。11000 表示的是红桃8（因为没有 0 号牌，所以000就表示8）。

第一步将扑克牌编码完成以后，第二步就需要找到一个序列，它必须满足以下的条件：由 $2^{n-1}$个1和$2^{n-1}$个0构成的序列或者圆排列，是否能存在在任意 n 个位置上0，1序列两两都不同。满足这个条件的序列也称为 n 阶完备二进圆排列。

这个魔术中我们需要找的是 5 阶完备二进圆排列。答案是存在这样一个满足条件的序列。这个序列也就是文章的主角，德布鲁因序列。

上述序列就是一个窗口大小为5的德布鲁因序列。任意连续的5个二进制相互之间都是两两不同的。所以给观众任意洗牌，不管怎么洗牌，只要最终挑出来是连续的5张，这5张的组合都在最终的结果之中。

将窗口大小为5的德布鲁因序列每5个二进制位都转换成扑克牌的编码，如下：

所以32张牌的初始顺序如下：
梅花8，梅花A，梅花2，梅花4，黑桃A，方片2，梅花5，黑桃3，方片6，黑桃4，红桃A，方片3，梅花7，黑桃7，红桃7，红桃6，红桃4，红桃8，方片A，梅花3，梅花6，黑桃5，红桃3，方片7，黑桃6，红桃5，红桃2，方片5，黑桃2，方片4，黑桃8，方片8。

上面这32张牌的初始顺序魔术师是要记在心里的。

将所有的排列组合列举出来，如上图。当魔术师让黑色或者红色的牌的人出列的时候，就能确定到具体是哪一种组合了。于是也就可以直接说出每个人手上拿的是什么牌了。

这个魔术中选取的德布鲁因序列也非常特殊，是可以通过一部分的递推得到。

这个特殊的序列，任意取出其中一个窗口，即5个连续的二进制，5个二进制的第一位和第三位，或者倒数第三位和倒数第五位相加，加法遵循二进制规则，即可得到这个窗口紧接着的下一位。

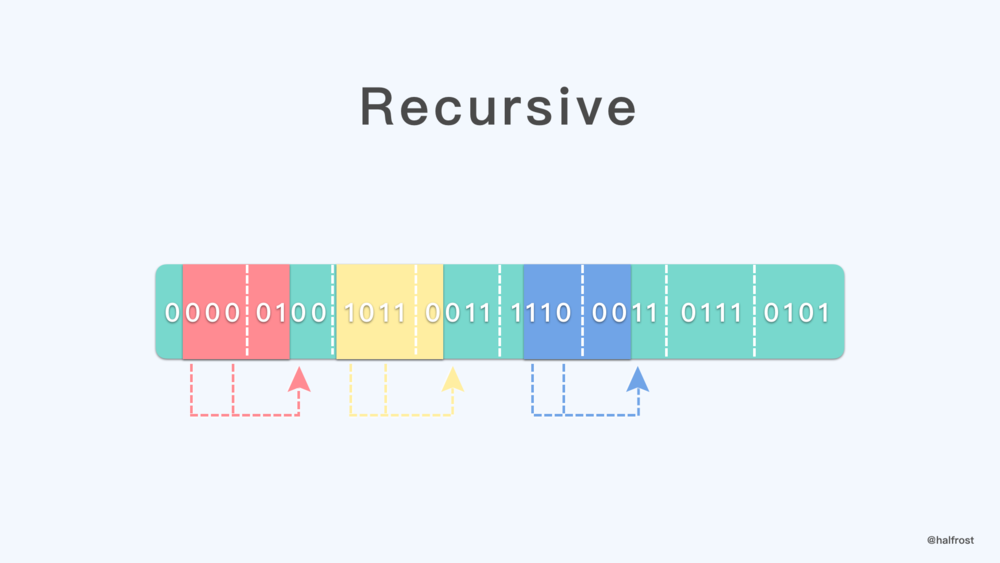
如上图的例子，假设当前窗口里面的五位是 00001，左数第一位加上第三位，或者右数第三位加上第五位，得到的是0，那么这个窗口紧接着的后一位就是0 ，即 000010 。再举一个例子，当前窗口里面是 11000 ，左数第一位加上第三位为1，所以紧接着的下一位是1，即 110001 。

最后一个关键的地方就在切牌的手法上。由于德布鲁因序列是一个循环的序列，为了维护这个序列，切牌只能把上面的牌切到下面去，不能乱切。只有上面的牌切到下面，因为循环的原因，这样才不能影响德布鲁因序列。

魔术能成功实施，必要条件就是要先记住32张牌的初始位置。然后切牌的时候暗示观众牌是洗过的。最后根据观众拿了黑色花色的牌(梅花和黑桃)举手，快速定位到5个连续的牌位于32张牌的哪个窗口，然后说出这5张牌的花色和点数。

三. 德布鲁因序列的定义和性质

• 定义

德布鲁因序列(De Bruijn sequence)，记为$B(k, n)$，是 k 元素构成的循环序列。所有长度为 n 的 k 元素构成序列都在它的子序列（以环状形式）中，出现并且仅出现一次。

例如，序列 00010111 属于B(2,3)。 00010111 的所有长度为3的子序列为000,001,010,101,011,111,110,100，正好构成了 {0,1} 3 的所有组合。

• 长度

德布鲁因序列的长度为 $k^n$。

注意到，所有长度为 n 的 k 元素构成的序列总共有 $k^n$。而对于德布鲁因序列中的每个元素，恰好构成一个以此元素开头长度为 n 的子序列。所以德布鲁因序列的长度为 $k^n$ 。

• 数量

德布鲁因序列的数量 $B(k,n)$ 的数量为 $\frac{(k!) ^ {k^{n-1}}}{k^n}$ 。

在德布鲁因图中的汉密尔顿回路 即为 德布鲁因序列。

目前使用这种序列的三维重建原理是，利用该序列可以生成一组足够长的颜色编码，在某个长度之上的片段的颜色构成是唯一的。以彩色条纹作为基 本编码元素构成的De Bruijn序列空间编码图案中。由于在一定的窗口（空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此，某个点的编码值可以通过其临域获得。其中，包含一个完整的空间编码的像素数量（窗口大小）就决定了重建的精度）内的连续的条纹颜色组成的序列是唯一性的，只要在单幅图像正确提取出子窗口内条纹的色彩信息及排列的顺序，就可实现条纹的位置的解码。

利用De Brujin序列产生的彩色条纹，由于要解决摄像机获得的变形条纹与投影条纹的对应问题。因此，在设计彩色条纹序列时需要注意相邻条纹不能是同样的颜色。如果存在相邻条纹是颜色相同，条纹宽度根据计算机的显示分辨率确定。摄像机摄取的变形条纹上两个相邻的颜色相同的条纹宽度也许跟一个单独的条纹宽度是一样的，在此情形下，后续的解码工作无法确保能顺利进行。

由于彩色图像由R、G、B三种颜色分量构成，为准确识别条纹的颜色，只取某种颜色成分为0或1，即RGB三个颜色分量每个使用0或1两个亮度等级。这样利用二进制的方式能够构成彩色条纹的颜色为$p_i=(p_i^r,p_i^g,p_i^b)\in \{0,1\}^3$，共有8种颜色。若投影的颜色条纹序列为$P=(p_0,p_1,\cdots,p_N)$ ，共有$N+1$个颜色条纹。所有可能的颜色集合用二进制表示为$\{000,001,\cdots ,111\}$。

结构光编码过程中，由于要求相邻条纹颜色至少一个分量发生变化，则前一种颜色与二进制集合$\{001,010,\cdots ,111\}$的一项逐位进行异或（xor）可以保证产生的De Brujin序列中相邻条纹发生颜色改变。例如前一种颜色为010 表示绿色，与元素100 异或后为110 表示黄色。即

$$p_{i+1}=p_iXORd_i,d_i\neq [0,0,0]$$

条纹宽度根据计算机的显示分辨率确定。此外，影响编码图像质量的一个重要因素是条纹的粗细，投影的条纹越多，条纹越细，获得的物体三维信息就越多，物体重建精度也就越高。而条纹过细，信息不断增加也会使计算复杂，抵抗环境光噪声的能力越差，耗时长等问题。若要增加分辨率，需要通过使用更多颜色增加条纹编码图案的密度，这样按指定的7 种颜色构成De brujin 序列。

取n=7,窗口长度m=3，条纹总数为343，单位彩色条纹宽度为8个像素。如图所示为本实验条件下生成的基于7 元3 阶De Bruijn序列的彩色结构光编码图案，其中所有相邻条纹颜色不同，在得到的彩色条纹编码图案中，每相邻3 个条纹组成的子条纹序列在整个条纹序列中是唯一的。这样在在随后的解码过程中，根据一定窗口内连续条纹颜色组成的序列的唯一性来进行条纹匹配，实现解码。由于De Bruijn序列具有一定的随机性，因此生成的颜色序列并不唯一。

---

2.5、结构光编码小结

---

时间编码方案能够获得较高的空间分辨率和测量精度，但由于需要投影多幅图案，因而仅适用于静态场景的三维重建。

空间编码往往只需要投影一幅图案，可用于动态场景的三维重建，但空间分辨率相对较低。直接编码一般只需要投影一幅图案，并能达到较高的空间分辨率，但投影仪颜色带宽、测量表面颜色或深度的变化、摄像机误差及噪声敏感性能会制约系统的测量精度和应用场合。当只投影一幅图案时，可实现动态场景的实时三维重建，这时研究的主要目标则是图像细节信息的精确提取和定位，减少噪声干扰并提高解码精度与速度。降低投影过程的复杂程度与三维重建的精度一直都是矛盾的。也就是说，越精确的三维重建需要越多的投影图案。目前结构光编码方案的研究方向是在保证或提高精度和鲁棒性的前提下，进一步减少投影图案数目和提高算法解码精度与速度。

---

参考资料

---

【1】麻呱智能 相机参数标定（camera calibration）及标定结果如何使用 2018年01月24日
【2】祥知道 [图像]摄像机标定(2) 张正友标定推导详解 2015年03月30日
【3】Daisey_tang 点云概念与点云处理 2018年12月14日
【4】EasyGOOO 格雷码结构光的编码 2015年3月11日
【5】一缕殇流化隐半边冰霜 神奇的德布鲁因序列
【6】David LEE伊卡洛斯 结构光综述 2019年1月13日
【7】David LEE伊卡洛斯 第五讲：相机与图像 2018年2月4日
【8】龚亚非 基于编码结构光的三维重建系统研究 2014年5月29日
【9】白宏运 基于空间编码结构光的高精度三维重构关键技术研究 2018年3月
【10】叶于平 自动扫描系统中点云配准、融合以及纹理重建问题研究 2016年4月
【11】杨东学 标定原理总结 2019年1月29日