曼哈顿Manhattan距离 和 欧氏Euclidean距离

数学

---

0. 各种距离及python实现

1.曼哈顿距离

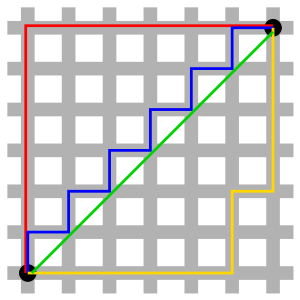
首先介绍一下曼哈顿，曼哈顿是一个极为繁华的街区，高楼林立，街道纵横，从A地点到达B地点没有直线路径，必须绕道，而且至少要经C地点，走AC和 CB才能到达。

由于街道很规则，ACB就像一个直角3角形，AB是斜边，AC和CB是直角边，根据毕达格拉斯(勾股)定理，或者向量理论，都可以知道用AC和CB 可以表达AB的长度。

在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的距离，则必须要进 行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

因此，计算机图形学就借用曼哈 顿来命名这一表示方法。
在我们常用的平面CAD中，都会有格点，他是基本单位，定义了格点大小后，就可以使用整数来表示和运算，不会引入计算误差，又快又精确。

如图：
$$

$$若已知 a 点 (x_1, y_1) 和 b 点 （x_2, y_2） 那么曼哈顿距离d就是$$

$$d = |x_1-x_2| + |y_2 - y_1|$$

2.欧式距离

其实就是直接算两点之间的距离，和来源于勾股定理的面积证明。

$$若已知 a 点 (x_1, y_1) 和 b 点 （x_2, y_2） 那么曼欧式距离d就是$$

$$d = \sqrt{ (x_1-x_2)^2 + (y_2 - y_1)^2 }$$

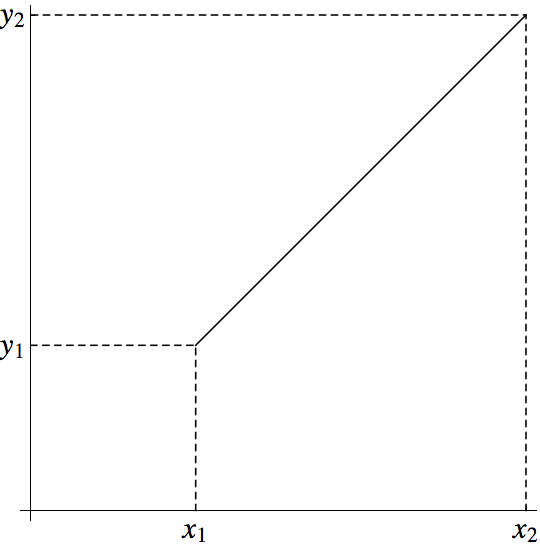
如果你有什么疑问，欢迎联系我哈，我会给大家慢慢解答啦~~~怎么联系我？ 笨啊~ ~~ 你留言也行
你关注微信公众号1.听朕给你说：2.tzgns666，3.或者扫那个二维码，后台联系我也行啦！

我祝各位帅哥，和美女，你们永远十八岁，嗨嘿嘿~~~

终于写完了，赞赏一下下嘛！

（爱心.gif） 么么哒~么么哒~么么哒
爱心从我做起，贫困山区捐衣服，为开源社区做贡献！

码字不易啊，如果你觉得本文有帮助，三毛也是爱！真的就三毛，呜呜。。。