排序

java

一、内排序

内排序是指所有的数据都已读入内存， 在内存中进行排序的算法。排序过程中不需要对磁盘进行读写。同时，内排序也一般假定所有用到的辅助空间也可以直接存入内存中。

1.归并（Merge Sort)

思想：归并排序是典型的分治思想。将线性数据结构分成两个部分，分别对这两个部分进行排序，排序完成后，再将各自排好序的部分合成一个有序的数组。

实例代码：

    public void sort(int[] array, int[] helper, int left, int right) {
        if(left >= right)
            return ;
        //防止溢出
        int mid = left + (right - left) / 2;
        sort(array, helper, left, mid);
        sort(array, helper, mid + 1, right);
        //合并左右两部分
        int helperLeft = left;
        int helperRight = mid + 1;
        int cur = left;
        for(int i = left; i <= right; i++) {
            helper[i] = array[i];
        }
        while(helperLeft <= mid && helperRight <= right) {
            if(helper[helperLeft] <= helper[helperRight]) {
                array[cur++]  = helper[helperLeft++];
            }else {
                array[cur++] = helper[helperRight++];
            }
        }
        while(helperLeft <= mid) {
            array[cur++] = helper[helperLeft++];
        }
    }

空间复杂度：需要一个helper[n]的辅助空间，故为O(n)

时间复杂度：每一趟归并的时间复杂度为O(n), 共需要进行log2n, 因此复杂度为O(nlogn)

动画演示参见右边连接: Comparison Sorting Algorithms

2.快速排序（Quick Sort)

思想：快速排序也是一种分治思想。它是随机选择一个元素作为轴值，利用该轴值将数组分为左右两部分，左边的元素都比轴值小，右边的都比轴值大，但它们是不完全排序的。在此基础上，再分别对分出来的左右两部分递归以上操作。

实例代码：

public void sort(int[] array, int left, int right) {
        if(left >= right)
            return ;
        int index = partition(array, left, right);
        sort(array, left, index - 1);
        sort(array, index + 1, right);
    }
    private int partition(int[] array, int left, int right) {
        int pivot = array[right];
        while(left != right) {
            while(array[left] < pivot && left < right) 
                left++;
            if(left < right) {
                int temp = array[right];
                array[right] = array[left];
                array[left] = temp;
                right--;
            }
            while(array[right] > pivot && right > left) {
                right--;
            }
            if(right > left) {
                int temp = array[left];
                array[left] = array[right];
                array[right] = temp;
                left++;
            }
        }
        array[left] = pivot;
        return left;
    }

空间复杂度：由于quick sort是递归的，需要借助一个工作栈来保存每一层递归调用的信息，其容量与递归调用的最大深度一致。最好情况下为O(log2_(n+1)), 最坏情况下为O(n), 平均情况下，栈的深度为O(log2_n)

时间复杂度：快速排序的运行时间与划分是否对称有关。最坏情况下发生在两个区域分别包含n-1个元素和0个元素，即对应初始排序就是基本有序或者逆序的状态，为O(n^2)。最好的情况下，就是划分后左右两部分大小都不大于n/2, 复杂度为O(nlog2_n)

动画演示参见右边连接: Comparison Sorting Algorithms

拓展: 利用快速排序思想，实现quick select。在平均复杂度为O(n)时间内从一个无序数组中返回第k大的元素

快速排序中，并不产生有序子序列，但每一趟排序，都会将一个元素放到他的最终位置上

实例代码：

public int selection(int[] array, int left, int right, int k) {
        if(left >= right)
            return array[left];
        int index = partition(array, left, right);
        int size = index - left + 1;
        if(size == k)
            return array[left + size - 1];
        else if(size > k) {
            return selection(array, left, index - 1, k);
        }else 
            return selection(array, index + 1, right, k - size);
    }

3.桶排序（Bucket Sort)

思想：桶排序是事先知道了待排序数组的一些基本信息（最大，最小范围），然后将数组放入有限的桶中，然后再分别对每个桶进行排序。然后再从桶中取出，形成有序序列。

下面给出一个例子，示意图来源：bubkoo的博客

设有数组 array = [29, 25, 3, 49, 9, 37, 21, 43]，那么数组中最大数为 49，先设置 5 个桶，那么每个桶可存放数的范围为：0~9、10~19、20~29、30~39、40~49，然后分别将这些数放人自己所属的桶。

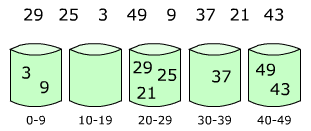
然后，分别对每个桶里面的数进行排序，或者在将数放入桶的同时用插入排序进行排序。最后，将各个桶中的数据有序的合并起来，如下图：

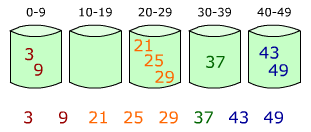
实例代码：以最简单的方式，每个桶就放一个数

    public void sort(int[] array, int n, int max) {
        int tempArray[] = new int[n];
        int i;
        for (i = 0; i < n; i++)
            tempArray[i] = array[i];
        int[] count = new int[max];
        for (i = 0; i < n; i++) { // 将元素放入桶中
            count[array[i]]++;
        }
        for (i = 1; i < max; i++) {
            count[i] = count[i - 1] + count[i]; 
            // count[i] 存的是 i+1 的值在原数组中开始的索引位置
        }
        for (i = n - 1; i >= 0; i--)
        //tempArray[i]的值在原数组中的下标应该是count[tempArray[i]] - 1
            array[--count[tempArray[i]]] = tempArray[i];
    }

空间复杂度：本例中就是O(max + n)

时间复杂度：桶排序的时间复杂度取决于各个桶之间数据进行排序的时间复杂度，即为O(n)

4.基数排序(Radix Sort)

思想：简单来说，基数排序就是对每一位数，都做一遍桶排序。

实例代码

    public void sort(int[] array, int n, int digits, int radix) {
        int radixModulo = 1; // radix modulo
        int[] tempArray = new int[n];
        int[] count = new int[radix];
        int digit;
        for(int i = 1; i <= digits; i++) {
            //每次初始化桶    
             for (int j = 0; j < radix; j++)
                    count[j] = 0;      
            //put the element into bucket
            for(int j = 0; j < n; j++) {
                digit = (array[j] / radixModulo) % radix;
                count[digit]++;
            }
            //桶排序
            for(int j = 1; j < radix; j++) {
                count[j] = count[j - 1] + count[j];
            }
            for(int j = n - 1; j >= 0; j--) {
                digit = (array[j] / radixModulo) % radix;
                count[digit]-= 1;
                tempArray[count[digit]] = array[j];
            }
            for(int j = 0; j < n; j++) {
                array[j] = tempArray[j];
            }
            radixModulo *= radix;
        }
    }

动画演示参见右边连接: RadixSort

二、外排序

内存中无法保存全部数据，需要进行磁盘访问，每次读入部分数据到内存中进行排序。

思想： 假设文件需要分成K块读入， 需要从小到大排列

1. 依次读入每个文件块，在内存中应用恰当的算法对当前文件块排序。此时，每个文件块相当于一个有小到大排列的序列。
2. 在内存中建立一个最小值堆，读入每块文件的队头。
3. 弹出堆顶元素，如果元素来自第i块，则从第i块文件中补充一个元素到最小值堆。弹出的元素暂时存在数组中。
4. 当临时数组写满时，将数组写到磁盘里，并清空数组内容。
5. 重复3，4步，直到所有文件块读取完毕。

堆排序

• 关于堆：这里我们是指二叉堆这种数据结构。二叉堆是一种完全二叉树，它的特点是对于除了根节点的节点i, A[parent] >= A[i]或者 A[parent] <= A[i]

• 堆排序：如何利用堆这种数据结构进行排序

  • 将A构成一个大顶堆（即保证根节点值大于孩子节点值）
  • 此时根节点为最大值，取出根节点
  • 将剩下的数组元素重新建立成大顶堆， 返回上一步，直到所有元素都取完

实例代码

建立大顶堆

//构造一个初始大顶堆, 从第一个非叶子结点开始
    private void maxHeapify(int[] array, int index) {
        //求下标从0开始的左右孩子下标
        int left = 2 * index + 1;   
        int right = 2 * index + 2;
        int max = 1;            //the init index
        if(left <= heapSize - 1 && array[left] > array[index]) {
            max = left;
        }else
            max = index;
        if(right < heapSize - 1 && array[right] > array[max]) {
            max = right;
        }
        //交换
        if(max != index) {
            int temp = array[max];
            array[max] = array[index];
            array[index] = temp;
            maxHeapify(array, max);
        }
    }

堆排序
为了使取出堆顶操作不破坏堆结构， 就将堆顶元素与数组最后一个元素交换。这样数组的第n个位置为有序，前n-1个位置为无序，然后再对无序的部分进行调整即可。

public void sort(int[] array) {
        for(int i = array.length - 1; i >= 1; i--) {
            int temp = array[i];
            array[i] = array[0];
            array[0] = temp;
            heapSize--;
            maxHeapify(array, 0);
        }
    }

空间复杂度：O(1)
时间复杂度：建堆时间是O(n), 每次调整的时间复杂度为O(h)。平均时间复杂度为O(nlogn)