机器学习——回归模型

机器学习

---

本文是一个机器学习新手对当前热门的机器学习的算法等的认识。

一、关于回归分析（Regression Analysis）

wiki上对于回归分析是这样描述的：回归分析是一种统计学分析数据的方法，目的在于了解两个或多个变数间是否相关、相关方向与强度，并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。

回归在数学上来说就是给定一个点集合，能够用一条曲线去拟合。根据曲线的差异也就分为线性回归，二次回归，Logistic回归等。

我们用Andrew Ng机器学习课程中给出的例子来说明一下回归。
我们给出一部分房屋的销售数据

Living area(feet^2)	Price
2104	400
1600	330
2400	369
...	...

下面是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。下面是回归模型的算法运行过程：

---

二、线性回归

回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面
1. 单个变量

$$y = ax + b$$

根据给出的样本，我们可以做个样本的分布图：

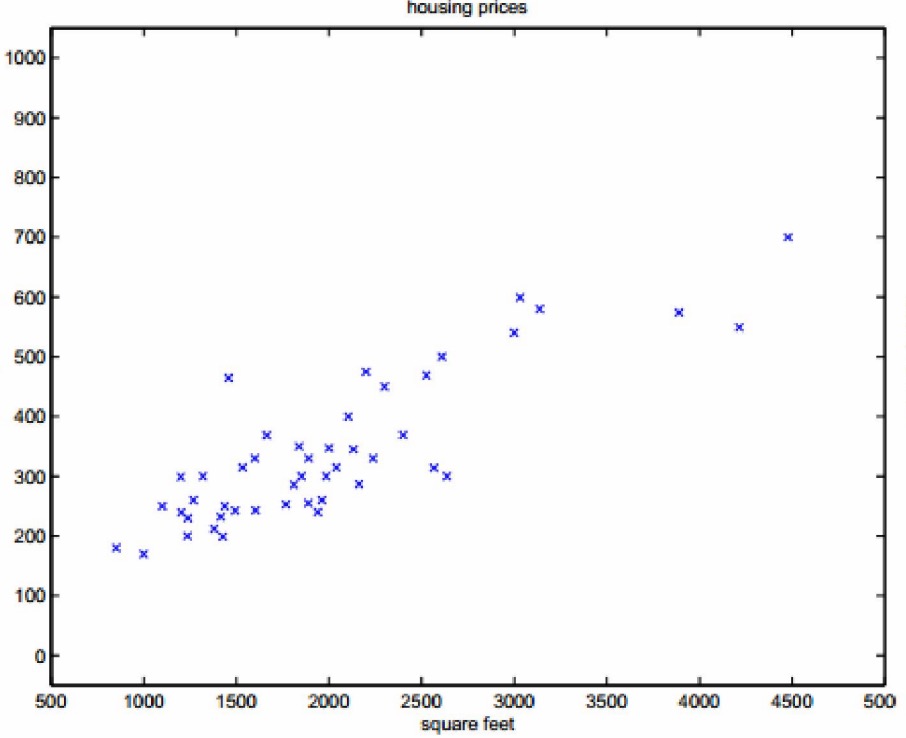
我们根据样本，可以估计拟合出一条曲线：

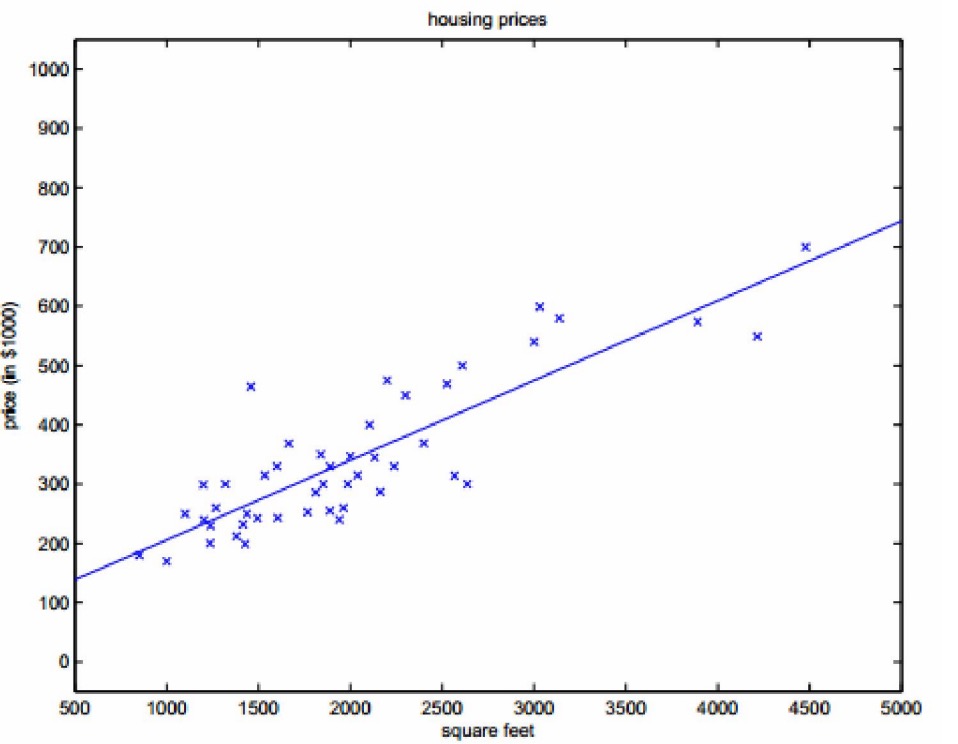
1. 考虑多个变量的情形

Living area(feet^2)	badrooms	Price
2104	3	400
1600	3	330
2400	2	369
...	...	...

我们给出线性拟合曲线如下，实际上是拟合了一个曲面

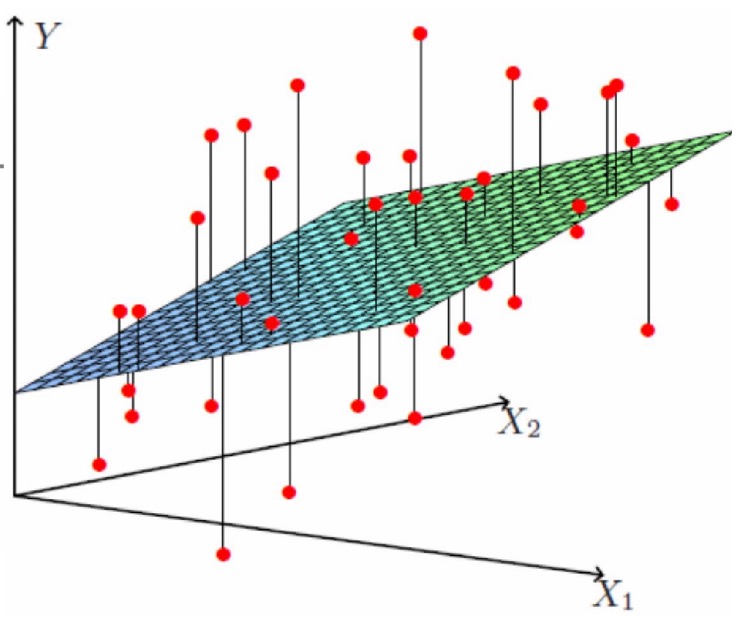
就此我们可以做出一个估计函数：

$$h_{\theta}(x) = \theta_{0} + \theta_{1}x + \theta_{2}x + \cdots + \theta_{n}x = \sum_{i = 1}^{n}\theta_{i}x_{i} = \theta^Tx(向量表示)$$

这样就给出了一个x与y的估计函数。现在我们假设第i个样本与真实值y之间存在一个误差，于是可以这样写：

$$y^i = \theta^Tx^i + \epsilon^i$$
现假设ϵ是独立同分布的， 服从与均值为0， 方差为σ2的正态分布（高斯分布）。
那么关于ϵ的概率密度函数就是：
$$\rho(\epsilon^i) = \frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(\epsilon^i)^2}{2\sigma^2}} = \frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(y^i - \theta^Tx^i)^2}{2\sigma^2}}$$

这样我们可以看成根据第i个样本来估计y的分布是怎样的：

$$\rho(y^i|x^i;\theta) = \frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(\epsilon^i)^2}{2\sigma^2}} = \frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(y^i - \theta^Tx^i)^2}{2\sigma^2}}$$

一个样本的概率密度是上面的公式， 那么M个样本的概率密度函数就是

$$L(\theta) = \prod_{i=1}^{m}\rho(y^i|x^i;\theta) = \prod_{i=1}^{m}\frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(y^i - \theta^Tx^i)^2}{2\sigma^2}}$$

上面的函数式子中，x与y都是已知的样本，θ是要学习的参数，因此L(θ)就是θ的似然函数。
下一步就是θ取什么值时，似然函数最大，也就是求极大似然函数
观察上面的公式， 直接取对数求驻点是计算量非常大的，因此我们把似然函数先取对数：

$$\iota(\theta) = logL(\theta)\\ = log\prod_{i=1}^{m}\frac{ 1 }{\sqrt{2\pi}\sigma} e^{-\frac{(y^i - \theta^Tx^i)^2}{2\sigma^2}}\\ = \sum_{i=1}^mlog\frac{ 1 }{\sqrt{2\pi}\sigma}e^{-\frac{(y^i - \theta^Tx^i)^2}{2\sigma^2}}\\ = mlog\frac{ 1 }{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\centerdot\frac{1}{2}\sum_{i=1}^m(y^i - \theta^Tx^i)^2$$

上面的公式取极大值，也就是下面的函数取极小值：

$$J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2$$

我们得到的这个函数称为代价函数（cost function），用来对h函数进行评估，描述h函数的不好程度。这个代价函数是对x(i)的估计值与真实值y(i)差的平方和作为代价函数。

下面我就求cost function的最小值

1.最小二乘法

对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

1. 用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
2. 用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
3. 最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

因此上面的损失函数cost function实际上就是最小二乘法， 即：

$$J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2$$

假设M个N维样本组成矩阵X，其中X的每一行对应一个样本共M个样本。
目标函数即为：

$$J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2\\ = \frac{1}{2}(X\theta - y)^T(X\theta - y)$$

要求这个目标函数的最小值，首先求其梯度：

$$\bigtriangledown_{\theta} J(\theta) = \bigtriangledown_{\theta}(\frac{1}{2}(X\theta - y)^T(X\theta - y))\\ =\bigtriangledown_{\theta}(\frac{1}{2}(\theta^TX^T-y^T)(X\theta - y)\\ =\bigtriangledown_{\theta}(\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty) \\ = \frac{1}{2}(2X^TX\theta-X^Ty-(y^TX)^T)\\ = X^TX\theta-X^Ty$$

让后求其驻点就可以得到解， 即：

$$X^TX\theta-X^Ty = 0$$
即得到
$$\theta = (X^TX)^{-1}X^Ty$$
以上就是利用最小二乘法得到的参数的解析式， 这样我们就可以根据给出得样本进行求解。

补充说明：

• 若XTX不可逆或防止过拟合，可以增加λ扰动
  

  $$\theta = (X^TX + \lambda I)^{-1}X^Ty$$
  因为XTX是一个半正定矩阵， 则对于任意λ>0, XTX+λI 肯定是正定矩阵。正定矩阵肯定是可逆的，因此使式子有意义。

• 实际上为了防止过拟合，可以在目标函数加上一个惩罚因子即：
  

  $$J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2 + \lambda\sum_{i=1}^m\theta_{i}^2$$
  把上面的式子通过梯度的计算，即可得到：
  $$\theta = (X^TX + \lambda I)^{-1}X^Ty$$

---

2.梯度下降(gradient descent)

实际过程中利用最小二乘法求解问题的时间复杂度太高，因此实际中使用有局限性，这个时候可以用梯度下降的方法。

梯度下降实际上就是沿着梯度下降的方向求解极小值得过程，同理也可以沿着梯度上升的方法求极大值

利用梯度下降法求解目标函数的过程：

$$J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2$$

1. 首先初始化θ， 可以随机初始化，也可以让θ为一个零向量
2. 改变θ的值，使目标函数按照梯度下降的方向进行值减小， 即首先对J(θ)对θ求一个偏导，然后沿着这个方向走一个减小的步长，即：
   $$\theta_{j} := \theta_{j} - \alpha\frac{\partial}{\partial\theta_{j}}J(\theta)$$

根据上面的目标函数，我们对一个样本求一下θ一阶偏导：

$$\frac{\partial}{\partial\theta_{j}}J(\theta) = \frac{\partial}{\partial\theta_{j}}\frac{1}{2}(h_{\theta}(x) - y)^2\\ = 2 \centerdot\frac{1}{2}(h_{\theta}(x) - y)\centerdot\frac{\partial}{\partial\theta_{j}}(h_{\theta}(x) - y)\\ =(h_{\theta}(x) - y)\centerdot\frac{\partial}{\partial\theta_{j}}(\sum_{i=0}^m\theta_ix_i - y)\\ =(h_{\theta}(x) - y)x_j$$

接下来我们给定一个学习率α来迭代更新θ的值，这里有两种策略

1. 批处理梯度下降
   批处理方式顾名思义，就是对全部样本求完后下降一次，即
   $$\theta_{j} := \theta_{j} - \alpha\sum_{i=1}^m(h_{\theta}(x^i) - y^i)x_j^i$$
2. 随机梯度下降
   对于随机梯度下降就是每扫描一个样本都更新一次θ，即
   $$Loop\ \ \{ \\ for \ \ i \ \ =\ \ 1\ \ to \ \ m,\ \ \{ \\ \ \ \ \ \ \ \ \ \theta_{j} := \theta_{j} - \alpha(h_{\theta}(x^i) - y^i)x_j^i \ \ \}\\ \}$$

补充说明
对于梯度下降方法，从某个初始点开始，沿着梯度下降（上升）得到是一个局部最小值（最大值），而不一定能得到全局的最值。然而对于凸(convex)函数，则一定能够收敛到一个全局最值上。对于线性回归而言，它的目标函数是一个二次函数，因此可以用梯度下降求解问题

---

3.实验

三、Logistic回归

利用Logistic解决分类问题

四、SoftMax回归