树的常见算法（一）

java

一、二叉树（Binary Tree)

二叉树的基本知识

• 二叉树是一种树形结构，其特点是每个结点至多只有两颗子树，并且二叉树的子树有左右之分。
• 非空二叉树叶子结点数等于度为2的结点的个数加1，即N0 = N2 + 1
• 非空二叉树上第K层上至多有2^(k-1)个结点。
• 高度为H的二叉树至多有2^H - 1个结点

二叉树定义：

public class TreeNode<T> {
    TreeNode<T> left;
    TreeNode<T> right;
    TreeNode<T> parent; //可以没有
    T element;
    public TreeNode(T element) {
        this.element = element;
        left = null;
        right = null;
        parent = null;
    }
}

以上是一个简单的二叉树结点的定义。

二叉树的遍历：

• 前序遍历（递归）：

public void preOrder(TreeNode<T> node) {
        if(node == null)
            return;
        print(node);
        preOrder(node.left);
        preOrder(node.right);
    }

• 前序遍历（非递归）：

public void preOrederNotRecursive(TreeNode<T> node) {
    TreeNode<T> cur = node;
    LinkedList<TreeNode<T>> stack = new LinkedList<TreeNode<T>>();
    while(node != null || !stack.isEmpty()) {
        while(cur != null) {
            //print
            print(cur);
            stack.push(cur);
            cur = cur.left;
        }
        if(!stack.isEmpty()) {
            cur = stack.pop();
            cur = cur.right;
        }
    }
}

为了得到前序的这种遍历顺序，利用辅助栈实现。
前序周游的非递归实现实际是在指针迭代的时候去打印结点。

• 中序遍历（递归）：

public void inOrder(TreeNode<T> node) {
    if(node == null)
        return ;
    inOrder(node.left);
    //print
    print(node);
    inOrder(node.right);
}

• 中序遍历（非递归）：

public void inOrderNotRecursive(TreeNode<T> node) {
    TreeNode<T> cur = node;
    LikedList<TreeNode<T>> stack = new LikedList<TreeNode<T>>();
    while(cur != null || !stack.isEmpty) {
        while(cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        if(!stack.isEmpty()) {
            //print stack top
            cur = stack.pop();
            print(cur);
            cur = cur.right;
        }
    }
}

中序遍历的非递归实现方法与前序的代码结构基本相同，但是中序实际上是打印栈顶元素。

• 后序遍历（递归）：

public void postOrder(TreeNode<T> node) {
    if(node == null)
        return ;
    postOrder(node.left);
    postOrder(node.right);
    //print
    print(node);
}

• 后序遍历（非递归）：

public void postOrderNotRecursive(TreeNode<T> node) {
    TreeNode<T> cur = node;
    //设置一个标记结点，用来确定是第几次访问栈顶元素
    TreeNode<T> flag = null;
    LinkedList<TreeNode<T>> stack = new LinkedList<TreeNode<T>>();
    while(cur != null || !stack.isEmpty()) {
        if(cur != null ) {
            stack.push(cur);
            cur = cur.left;
        }else {
            cur = stack.peek();
            //判断栈顶元素是否是第一次出现，以压入其右子树
            if(cur.right != null && cur.right != flag) {
                cur = cur.rigth;
                stack.push(cur);
                //return to left
                cur = cur.left;
            }else {
                cur = stack.pop();
                //print
                print(cur);
                flag = cur;
                cur = null;
            }
        }
    }
}

后序遍历的非递归实现：对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还为被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

一、二叉搜索树（Binary Search Tree)

二叉搜索树的基本知识

二叉查找树或者是一颗空树，或者是一颗具有以下特性的非空二叉树：

• 若左子树非空，则左子树所有结点关键字值均小于根结点关键字的值
• 若右子树非空，则右子树所有结点关键字值均小于根结点关键字的值
• 左，右子树本身也是一个二叉搜索树（BST）

BST相关算法

算法一：判断一个树是否为BST

思路：中序遍历一个BST会得到一个有序的递增序列，可以利用此性质判断一颗二叉树是否为BST。

private int compare(T e1, T e2) {
        return e1.compareTo(e2);
    }
public boolean isBST(TreeNode<T> root, T max, T min) {
        return isBSTHelper(root, max, min);
    }

利用一个辅助函数，引入最大值最小值思想：

• 左子树的所有结点值在min与根结点之间
• 右子树的所有结点值在根与max之间

public boolean isBSTHelper(TreeNode<T> root, T max, T min) {
        if(root == null)
            return true;
        if(   compare(root.element, max) < 0 || (compare(root.element, max) == 0 && root.right == null)
           && compare(root.element, min) > 0 || (compare(root.element, min) == 0 && root.left == null)
           && isBSTHelper(root.left, root.element, min)
           && isBSTHelper(root.right, max, root.element)) {
            return true;
        }
        return false;
    }

算法二：BST的插入（insert），删除（delete），查找（search）

• Insert: BST的插入过程是一个递归过程，如果插入结点值比插入位置结点值小，则插入到左子树。反之则插入到右子树中。若插入位置结点的左子树或者右子树为空，则直接插入。

public void insert(TreeNode<T> node, T ele) {
        if(ele.compareTo(node.element) == -1) {
            if(node.left != null) {
                insert(node.left, ele);
            }else {
                node.left = new TreeNode<T>(ele);
            }
        }else {
            if(node.right != null) {
                insert(node.right, ele);
            }else {
                node.right = new TreeNode<T>(ele);
            }
        }
    }

• Delete: BST的删除结点后为了扔保证是BST, 需要分为3种情况处理：
  1.如果被删除结点是叶子结点，则直接删除。

  2.如果被删除结点p只有一颗左子树或者右子树，则让该结点p的子树直接变成其父节点的孩子。例如：
  
  删除结点18， 根据以上描述，应变为
  

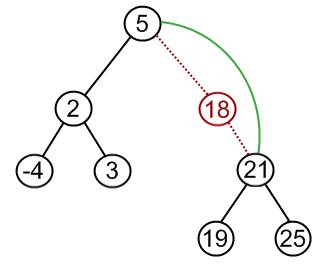
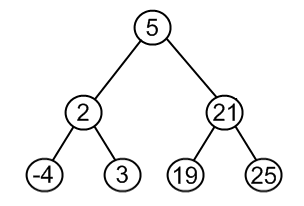
3.如果被删除结点p有左、右两颗子树，则让p的右子树上中序第一个子女，也就是右子树上的最小值来填补p。这样就装换成了第1种和第2种情况了。例如：
删除结点12，这个结点存在左右孩子

找到右子树的最小值，来替代被删除结点，转而删除这个替代的结点即可

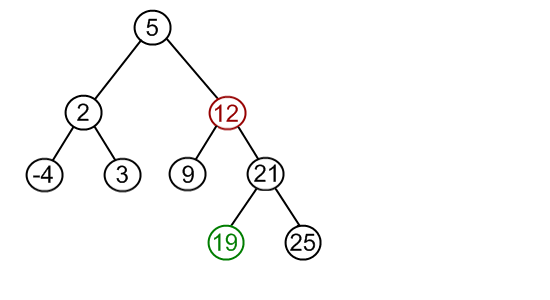
递归找到替代结点，删除即可，又变成了第1或者第2种情况。

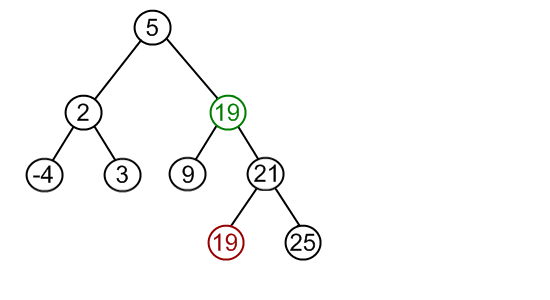
public void delete(T val) {
        root = delete(root, val);
}

/**
     * @param the node that the root  
     * @param the item to remove
     * @return the new root
     */
    public TreeNode<T> delete(TreeNode<T> node, T val) {
        if(node == null)
            return node;
        else {
            if(val.compareTo(node.element) < 0) {
                node.left = delete(node.left, val);
            }else if(val.compareTo(node.element) > 0) {
                node.right = delete(node.right, val);
            }else {
                //two children
                if(node.left != null && node.right != null) {
                    node.element = findMin(node.right).element;
                    node.right = delete(node.right, node.element);
                }else {
                    node = (node.left != null) ? node.left : node.right;
                }
            }
        }
        return node;
    }

//find min node
    public TreeNode<T> findMin(TreeNode<T> node) {
        if(node.left == null)
            return node;
        else 
            return findMin(node.left);
    }

• search: 根据bst的顺序性质，只需要遍历bst即可：

public boolean search(T val)    {
        TreeNode<T> r = root;
        while(val.compareTo(r.element) != 0) {
            if(val.compareTo(r.element) < 0) {
                r = r.left;
            }else {
                r = r.right;
            }
            if(r == null)
                return false;
        }
        return true;
    }

算法三：判断一颗二叉树或者一颗bst是否是平衡树

思路：考虑平衡树的一些特点

• 空树也是平衡树。
• 左子树和右子树的高度差绝对值不超过1
• 左子树和右子树也是平衡的

public boolean isBanlanced(TreeNode<T> root) {
        if(root == null) 
            return true;
        int res = Math.abs(height(root.left) - height(root.right));
        return res < 2 && isBanlanced(root.left) && isBanlanced(root.right);
    }

//return the tree's height
public int height(TreeNode<T> root) {
        if(root == null)
            return 0;
        return Math.max(height(root.left), height(root.right)) + 1;
    }

另外给出一种判断平衡树的优化做法:
isBanlancedHelper返回当前结点的高度， 将计算结果自底向下向上传递,确保每个结点只被计算一次。O(n)

public boolean isBanlancedEffective(TreeNode<T> root) {
        return (-1 != isBanlancedHelper(root));
    }
private int isBanlancedHelper(TreeNode<T> root) {
        if(root == null)
            return 0;
        int lheight = isBanlancedHelper(root.left);
        if(lheight == -1)
            return -1;
        int rheight = isBanlancedHelper(root.right);
        if(rheight == -1)
            return -1;
        if(Math.abs(lheight - rheight) > 1) {
            return -1;
        }
        return Math.max(lheight, rheight) + 1;
    }

算法四：将一个sortArray 转化为bst

用java做还是比较容易的

算法五：Find Next

分别给出preOrder, inOrder, postOrder, levelOrder的后继结点的求出方法。

InOrderSuccessor: 若该结点的右子树存在，则它的后继就是其右子树中最左边的结点，也就是右子树中最小的结点。
遍历bst，找到该结点，则第一个比它大的即为后继结点

public TreeNode<T> inOrderSuccessor(TreeNode<T> node) {
        if(node == null)
            return null;
        if(node.right != null) {
            return leftMostNode(node.right);
        }
        TreeNode<T> successor = null;
        TreeNode<T> cur = root;
        while(cur != null) {
            if(node.element.compareTo(root.element) < 0) {
                successor = cur;
                cur = cur.left;
            }else {
                cur = cur.right;
            }
        }
        return successor;
    }

    private TreeNode<T> leftMostNode(TreeNode<T> node) {
        if(node == null) 
            return null;
        while(node.left != null) {
            node = node.left;
        }
        return node;
    }

preOrderSuccessor 大体思路：
主要问题就是要求后继的结点是一个叶子结点的话，需要提前知道它的祖先结点

• 如果这个结点有左子树，那么successor是它的左孩子
• 如果这个结点有右子树，那么successor是它的右孩子
• 如果这个结点是一个叶子结点，那么successor是它最近祖先结点的右孩子，并且此右孩子是未被访问过的。

    public TreeNode<T> preOrderSuccessor(TreeNode<T> node) {
        //null node
        if(node == null)
            return null;
        TreeNode<T> cur = root;
        TreeNode<T> ancesor = null;
        while(cur != null && node.element.compareTo(cur.element) != 0) {
            if(node.element.compareTo(cur.element) < 0) {
                if(cur.right != null) {
                    ancesor = cur;
                }
                cur = cur.left;
            }else {
                cur = cur.right;
            }
        }
        //can't find this node
        if(cur == null)
            return null;
        if(cur.left != null)
            return cur.left;
        if(cur.right != null)
            return cur.right;
        if(ancesor != null)
            return ancesor.right;
        return null;
    }

postOrderSuccessor 大体思路：后序遍历找当前结点p的后继时，p的下面的结点都在p的前面顺序出现，因此只需要关注p结点的parent结点即可。

• 如果p结点不是parent结点的右孩子，那么successor就是右子树中最左边的结点leftmost
• 如果p结点是parent的右孩子，那么parent结点就是successor

public TreeNode<T> postOrderSuccessor(TreeNode<T> node) {
        if(node == null)
            return null;
        if(node == root)
            return null;
        TreeNode<T> cur = root;
        TreeNode<T> parent = null;
        while(cur != null && node.element.compareTo(cur.element) != 0) {
            parent = cur;
            if(node.element.compareTo(cur.element) < 0) {
                cur = cur.left;
            }else {
                cur = cur.right;
            }
        }
        //find the node
        if(parent.right == cur) {
            return parent;
        }else {
            return leftMostNode(parent.right);
        }
    }

算法六：LCA，Lowest Common Ancestor

就是在一颗树中寻找两个结点p, q的公共祖先，例如下图：

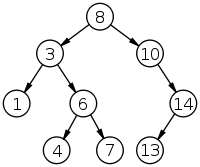
结点3， 10的公共祖先就是8。结点1， 13的公共祖先也是8

算法思路: 如果结点p, q都在某个结点左子树或者右子树，即在同一边上，那么它们的LCA也一定在左子树或者右子树上。这样就可以分解成相同的小规模去解决问题，运用递归。如果p, q在某个结点的两边，那么这个结点即为LCA

    public TreeNode<T> lowestCommonAncetor(TreeNode<T> root, TreeNode<T> p, TreeNode<T> q ) {
        if(lcaHelper(root.left, p) && lcaHelper(root.left, q)) {
            return lowestCommonAncetor(root.left, p, q);
        }
        if(lcaHelper(root.right, p) && lcaHelper(root.right, q)) {
            return lowestCommonAncetor(root.right, p ,q);
        }
        return root;
    }
    //判断结点p是否是某个在某个子树中
    private boolean lcaHelper(TreeNode<T> root, TreeNode<T> p) {
        if(root == null) {
            return false;
        }
        if(root == p)
            return true;
        return lcaHelper(root.left, p) || lcaHelper(root.right, p);
    }

算法七-：print Range

给定一个区间值，打印BST中所有在这个区间的结点的值
思路：bst运用中序遍历

//the range [start, end]
    public void printRange(TreeNode<T> root, T start, T end) {
        //assert start <= end 
        if(root == null)
            return ;
        //inOrder
        if(start.compareTo(root.element) < 0) {
            printRange(root.left, start, end);
        }
        if(start.compareTo(root.element) <= 0 && end.compareTo(root.element) >= 0) {
            System.out.print(root.element + " ");
        }
        if(end.compareTo(root.element) > 0) {
            printRange(root.right, start, end);
        }
    }