[关闭]
@pastqing 2016-03-18T13:41:15.000000Z 字数 4933 阅读 2509

树的常见算法（二）

java

一、前缀树（字典树）（Trie）

Trie根据wiki上定义，它是一种hash树的变种。典型应用在统计和排序大量字符串（但不仅限于字符串中），所以经常被用于搜索引擎中的统计词频。它的特点是最大限度地减少无谓的字符串比较，查询效率比较高。

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

它有3个基本性质：

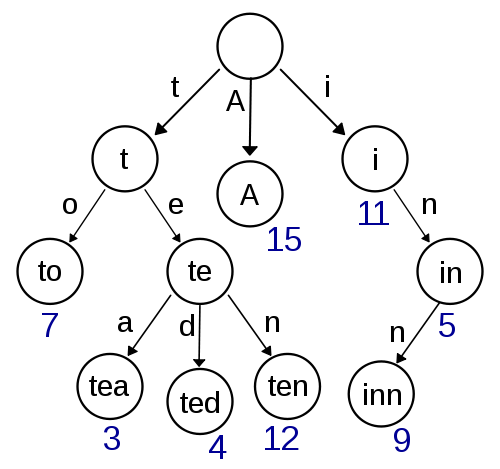
Trie的实现可以用数组和链表。使用数组的好处是对子结点查询快，但是每次都要分配26大小的数组空间，非常浪费。使用链表需要保存每个结点的兄弟结点的连接。使用链表可以很好的节约空间，但是查找效率不高。

下面使用数组实现一个简单的trie

Trie的数据结构定义

  1. private class TrieNode {
  3.         char content;
  5.         boolean marker;             //marker的作用是判断是否是这个单词的末尾
  6.         TrieNode[] child;
  8.         public TrieNode() {
  9.             content = ' ';
  10.             marker = false;
  11.             child = new TrieNode[26];
  12.         }
  13.     }

成员marker的作用是标记单词结尾，这样的作用是确保某个单词的子串不会被搜索到，在它未被插入trie树前。例如trie树已经插入单词manly, 但是man没被插入，这样可以保证man在搜索时不被搜索到。

Trie的简单实现

Insert(String s):

  1. public void insert(String s) {
  3.         TrieNode cur = root;
  4.         //empty string
  5.         if(s.isEmpty()) {
  6.             cur.marker = true;
  7.             System.out.println("String is empty");
  8.             return ;
  9.         }
  10.         for(int i = 0; i < s.length(); i++) {
  12.             char c = s.toLowerCase().charAt(i);
  13.             if(cur.child[c - 'a'] == null) {
  14.                 cur.child[c - 'a'] = new TrieNode(c - 'a');
  15.             }
  16.             cur = cur.child[c - 'a'];
  18.             if(i == s.length() - 1) {
  19.                 cur.marker = true;
  20.             }
  21.         }
  22.         System.out.println("Insert word: " + s);
  23.     }

search(String t):

  1. public boolean search(String t) {
  2.         if(t.isEmpty()) {
  3.             return false;
  4.         }
  5.         TrieNode cur = root;
  6.         while(cur != null) {
  7.             for(int i = 0; i < t.length(); i++) {
  8.                 char c = t.toLowerCase().charAt(i);
  9.                 if(cur.child[c - 'a'] == null) {
  10.                     return false;
  11.                 }else {
  12.                     cur = cur.child[c - 'a'];
  13.                 }
  14.             }
  15.             return cur.marker;
  16.         }
  17.         return false;
  18.     }

delete(String s):

  1. public boolean delete(String t) {
  2.         if(t.isEmpty())
  3.             return false;
  5.         TrieNode cur = root;
  6.         //TrieNode lastMarker = null;
  7.         if(root != null) {
  8.             ArrayList<TrieNode> temp = new ArrayList<TrieNode>();
  9.             for(int i = 0; i < t.length(); i++) {
  10.                 cur = cur.child[t.charAt(i) - 'a'];
  11.                 temp.add(cur);
  12.                 if(cur.marker && i != t.length() - 1) {
  13.                     temp.clear();
  14.                 }
  15.             }
  16.             for(TrieNode tr : temp) {
  18.                 tr.content = ' ';
  19.                 tr.marker = false;
  20.             }
  21.             temp.clear();
  22.             temp = null;
  23.         }
  24.         return false;
  25.     }

二、红黑树（RED-BLACK BST）

以下红黑树的知识介绍采用july的红黑树文章中的描述。

红黑树是一种自平衡的二叉搜索树（BST），本质上来说他是一个BST，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)

但它是如何保证一棵n个结点的红黑树的高度始终保持在h = logn的呢？这就引出了红黑树的5条性质：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。

正是红黑树的这5条性质，使得一棵n个结点是红黑树始终保持了logn的高度，从而也就解释了上面我们所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论的原因。

补充：如果每一条从根到null结点的路径都包含b个黑色结点，则树必须至少包含2^b - 1个黑色结点。又因为根也是黑色的，而且在路径上不能有两个连续的红色结点，因此红黑树的高度最多为2log(N+1)

红黑树的插入

红黑树的插入与bst的插入思路是一样的，即要插入一个结点p首先找到插入结点的位置，然后进行插入。具体做法请见我上一篇文章bst的插入

红黑树的插入相当于在二叉查找树插入的基础上，为了重新恢复平衡，继续做了插入修复操作。通常总是将新项作为叶子结点插入树中。如果将新项涂成黑色，则违反了性质5，因为将创建一条更长的黑色结点路径，因此必须将新项涂成红色。如果插入的如果插入的结点的父结点是黑色，由于此不会违反性质2和性质4，红黑树没有被破坏，所以此时也是什么也不做
伪代码如下

  1.    y ← nil[T]  
  2.    x ← root[T]  
  3.    while x ≠ nil[T]  
  4.        do y ← x  
  5.           if key[z] < key[x]  
  6.              then x ← left[x]  
  7.              else x ← right[x]  
  8.    p[z] ← y  
  9.    if y = nil[T]  
  10.      then root[T] ← z  
  11.      else if key[z] < key[y]  
  12.              then left[y] ← z  
  13.              else right[y] ← z  
  14.   left[z] ← nil[T]  
  15.   right[z] ← nil[T]  
  16.   color[z] ← RED  
  17.   INSERT-FIXUP(T, z)

但是遇到下面3种情况时：

下面具体分析每种情况：

插入修复情况1：如果当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色

此时父结点的父结点一定存在，否则插入前就已不是红黑树。
与此同时，又分为父结点是祖父结点的左子还是右子，对于对称性，我们只要解开一个方向就可以了。

在此，我们只考虑父结点为祖父左子的情况。
同时，还可以分为当前结点是其父结点的左子还是右子，但是处理方式是一样的。我们将此归为同一类。

对策：将当前结点的父结点和叔叔结点涂黑，祖父结点涂红，把当前结点指向祖父结点，从新的当前结点重新开始算法。

针对情况1，变化前[当前结点为4结点]：

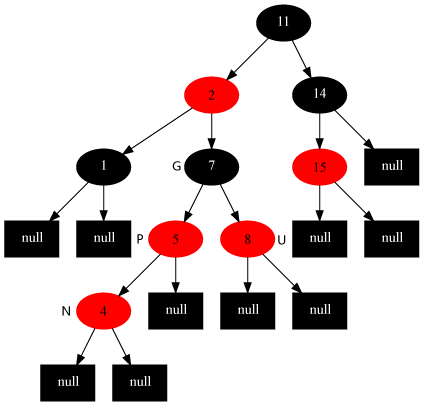
rb_1.png-9kB

变化后：
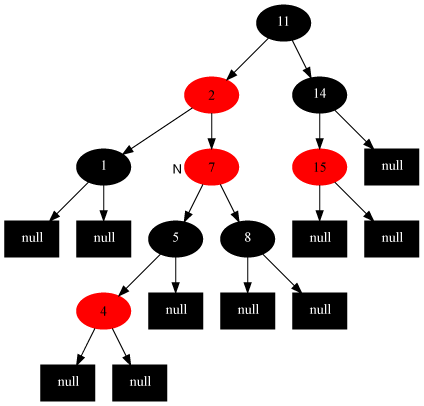
rb_2.png-8.7kB

插入修复情况2：当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的右子

对策：当前结点的父结点做为新的当前结点，以新当前结点为支点左旋

如下图所示，变化前[当前结点为7结点]
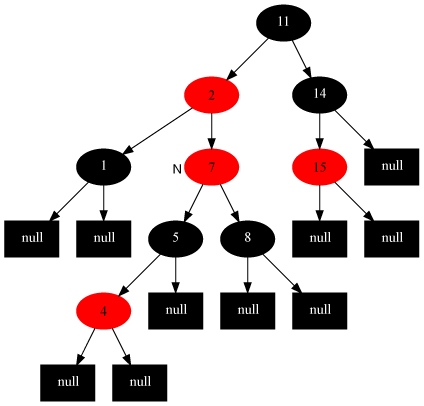
rb_3.png-8.7kB

变化后：
rb_4.png-8.9kB

插入修复情况3：当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的左子

对策：父结点变为黑色，祖父结点变为红色，在祖父结点为支点右旋，操作代码为：
最后，把根结点涂为黑色，整棵红黑树便重新恢复了平衡。
如下图所示[当前结点为2结点]
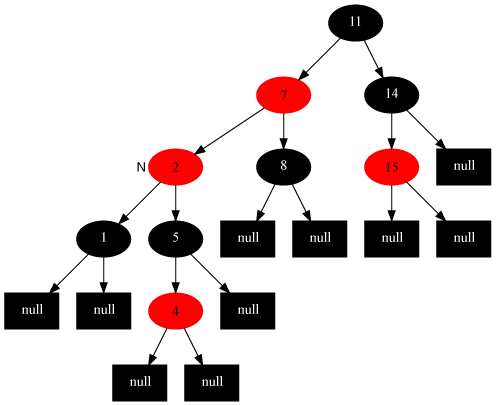
rb_5.png-8.9kB

变化后：
rb_6.png-8.2kB

红黑树的删除

我们删除的结点的方法与常规二叉搜索树中删除结点的方法是一样的，如果被删除的结点不是有双非空子女，则直接删除这个结点，用它的唯一子结点顶替它的位置，如果它的子结点分是空结点，那就用空结点顶替它的位置，如果它的双子全为非空，我们就把它的直接后继结点内容复制到它的位置，之后以同样的方式删除它的后继结点，它的后继结点不可能是双子非空，因此此传递过程最多只进行一次。

对于BST的如何删除，请参见我的上一篇文章bst的删除

下面具体分析红黑树删除的修复

在删除结点后，原红黑树的性质可能被改变，如果删除的是红色结点，那么原红黑树的性质依旧保持，此时不用做修正操作，如果删除的结点是黑色结点，原红黑树的性质可能会被改变，我们要对其做修正操作。那么哪些树的性质会发生变化呢，如果删除结点不是树唯一结点，那么删除结点的那一个支的到各叶结点的黑色结点数会发生变化，此时性质5被破坏。如果被删结点的唯一非空子结点是红色，而被删结点的父结点也是红色，那么性质4被破坏。如果被删结点是根结点，而它的唯一非空子结点是红色，则删除后新根结点将变成红色，违背性质2。

上面的修复情况看起来有些复杂，下面我们用一个分析技巧：我们从被删结点后来顶替它的那个结点开始调整，并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢，我们不是把红黑树的结点加上除红与黑的另一种颜色，这里只是一种假设，我们认为我们当前指向它，因此空有额外一种黑色，可以认为它的黑色是从它的父结点被删除后继承给它的，它现在可以容纳两种颜色，如果它原来是红色，那么现在是红+黑，如果原来是黑色，那么它现在的颜色是黑+黑。有了这重额外的黑色，原红黑树性质5就能保持不变。现在只要恢复其它性质就可以了，做法还是尽量向根移动和穷举所有可能性。

如果是以下情况，恢复比较简单：

但如果是一下情况，

下面具体分析这4种情况

删除修复情况1：当前结点是黑+黑且兄弟结点为红色(此时父结点和兄弟结点的子结点分为黑)。

解法：把父结点染成红色，把兄弟结点染成黑色，之后重新进入算法（我们只讨论当前结点是其父结点左孩子时的情况）。此变换后原红黑树性质5不变，而把问题转化为兄弟结点为黑色的情况(注：变化前，原本就未违反性质5，只是为了把问题转化为兄弟结点为黑色的情况)

变化前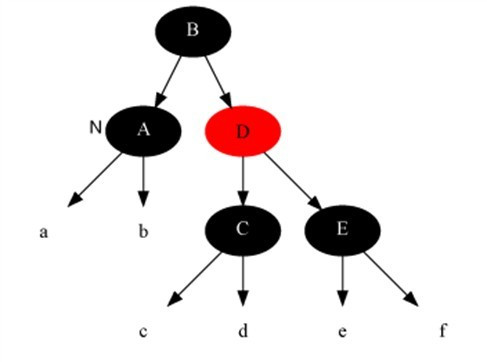：rb_7.jpg-14.3kB

变化后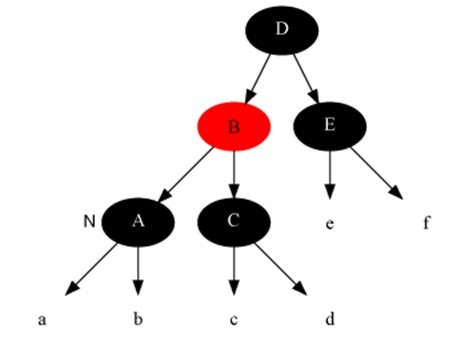：rb_8.jpg-13.3kB

删除修复情况2：当前结点是黑加黑且兄弟是黑色且兄弟结点的两个子结点全为黑色。

解法：把当前结点和兄弟结点中抽取一重黑色追加到父结点上，把父结点当成新的当前结点，重新进入算法

变化前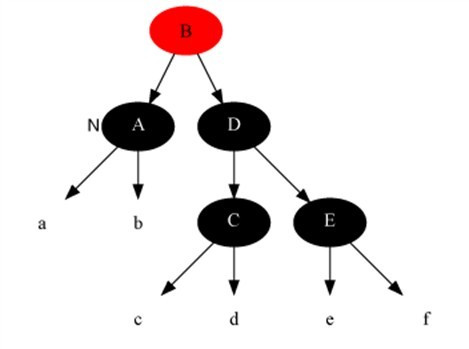：rb_9.jpg-13.3kB

变化后：rb_10.jpg-14.1kB

删除修复情况3：当前结点颜色是黑+黑，兄弟结点是黑色，兄弟的左子是红色，右子是黑色

解法：把兄弟结点染红，兄弟左子结点染黑，之后再在兄弟结点为支点解右旋，之后重新进入算法。此是把当前的情况转化为情况4，而性质5得以保持。

变化前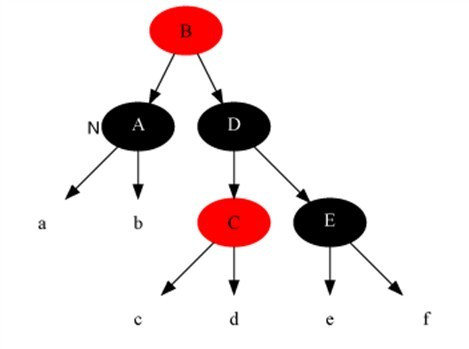：rb_11.jpg-14kB

变化后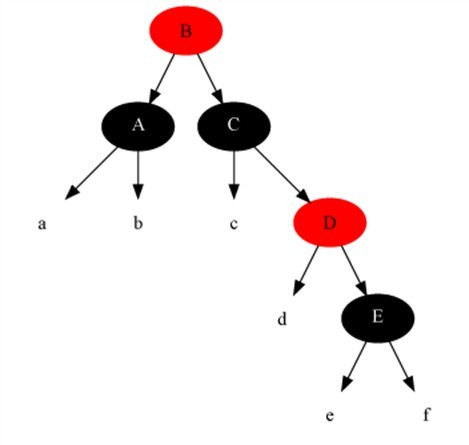：rb_12.jpg-14.7kB

删除修复情况4：当前结点颜色是黑-黑色，它的兄弟结点是黑色，但是兄弟结点的右子是红色，兄弟结点左子的颜色任意。

解法：把兄弟结点染成当前结点父结点的颜色，把当前结点父结点染成黑色，兄弟结点右子染成黑色，之后以当前结点的父结点为支点进行左旋，此时算法结束，红黑树所有性质调整正确。

变化前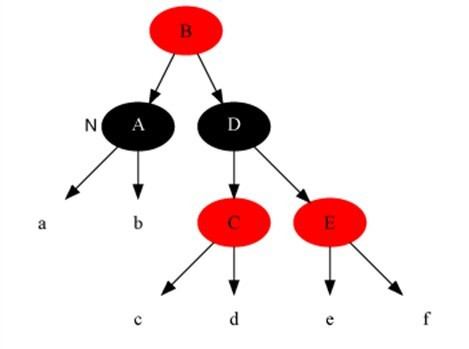：rb_13.jpg-14.8kB

变化后：rb_14.jpg-14.1kB

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注