ch5 特征值与特征向量 ‘线性代数及其应用笔记’

具体数学

---

5.1 特征向量与特征值

A为n维方阵，x为非零向量，若存在数$\lambda$使$Ax=\lambda x$成立，则称$\lambda$为A的特征值，x称为对应于$\lambda$的特征向量。

定理 三角矩阵的主对角线的元素是其特征值。
又一个定理 n维方阵A的各个特征向量组成的集合$\{v_1,v_2,...,v_r\}$线性无关。
证明：
特征向量和差分方程
对于方程$x_{k+1}=Ax_k$，这个方差使用递归来表示x序列，下面我们找出x的显式解，也就是x不依赖A和序列前面的项，而是依赖初始项。利用$Ax=\lambda x$,找出A的一个特征向量$x_0$并令$x_k=\lambda^kx_0$

5.2 特征方程

求特征值的基本思想是利用行列式把含有两个未知数的方程$(A-\lambda I)x=0$转化为只含有$\lambda$的方程。
首先要原方程x有非平凡解，那么$A-\lambda I$就是不可逆矩阵，就是说$A-\lambda I$的行列式为0。

回想一下求行列式方法，利用倍加和交换将其转换为阶梯形，那么行列式等于主对角线乘积乘以$(-1)^r$（r为行交换次数）。

那么很容易发现，阶梯形矩阵主对角线上的元素，如果可逆，那么都是主元，行列式不为0；若不可逆，那么主对角线上必有元素为0，则行列式为0。所以A可逆当且仅当行列式为不为0。再结合三角矩阵的主对角线的元素是其特征值，我们又可以得到可逆矩阵的又2条定理（天哪噜，好多定理了） ：
A是n维方阵，A是可逆的当且仅当：
1. 0不是A的特征值
2. A的行列式不等于零。

顺便我们也来总结下行列式性质：
1. A可逆当且仅当$detA\neq 0$
2. $detAB=(detA)(detB)$
3. $detA^T=detA$
4. 若A是三角形矩阵，则detA是A对角线元素乘积
5. 对A做行倍加不改变行列式，做一次行交换行列式变符号，数乘一行后行列式等于原值乘以此数。

插完回顾，我们得到以下结论：
数$\lambda$是n维方阵A的特征值得充要条件是$\lambda$是特征方程$det(A-\lambda I)=0$的根。
容易得出特征方程左边是n次多项式，称为A的特征多项式。
若特征多项式中$(\lambda - k)$出现n次，则称特征值k有重数 n。
这里插一句，特征值允许有复根，称为复特征值，但是一般我们只考虑实特征根。
下面是特征值的一个用途，相似性

A，B都是n维方阵，若存在可逆矩阵P，使得$P^{-1}AP=B$，则称A相似于B，或A和B是相似的，把A变为$P^{-1}AP$的变换称为相似变换。 相似矩阵有着相同的特征多项式，从而有相同的特征值（和重数）。（通过证明$det(A-\lambda I)=det(B-\lambda I)$得到）

5.3 对角化

利用分解式$A=PDP^{-1}$，我们能在k较大时快速算出$A^k$。D代表对角矩阵，容易得

$$若D=\begin{bmatrix}a &0\\0&b \end{bmatrix} \\则 D^{k}=\begin{bmatrix}a^k &0\\0&b^k \end{bmatrix}$$
那么容易得出 $$A^k=PD^kP^{-1}$$
对角化定理
n维方阵A可对角化的充要条件是A有n个线性无关的特征向量。
换句话说，A可对角化当且仅当有足够特征向量形成$\mathbb{R}^n$的基，我们称这样的基为特征向量基。

在证明过程中我们可以发现，A的对角矩阵D的主对角线元素即为A的特征值，P的列即为A的特征向量。
那么确定一个矩阵可以对角化之后我们看看如何对角化：
对角化步骤
1. 求出A的特征值
2. 求A的线性无关的特征向量
3. 用第2步得到的向量构造矩阵P
4. 用对应的特征值构造矩阵D

在求的时候我们可以看出一个可对角化的充分条件，就是n维矩阵有n个相异的特征值。n个相异的特征值能保证n个线性无关的特征向量。当相异特征值个数小于n时，只要每个特征值$\lambda_k$的特征空间维数等于$\lambda_k$的代数重数，那么也可以保证A可对角化。

这里加一个对角化和线性变换
原来是5.4的内容，但是加在这里更好一点
如果$A=PDP^{-1}$。D为n维对角矩阵，若$\mathbb{R}^n$的基B由P的列向量组成，那么D是变换x->Ax的B-矩阵。

5.4 特征向量与线性变换

线性变换矩阵
设V是n维向量空间，W是m维向量空间，T是V到W的线性变换，B/C分别是V/W的基。 那么有：

$$[T(x)]_C=M[x]_B \\ 其中 M=[[T(b_1)]_C\ ...[T(b_n)]_C]$$
如果不能理解可以看这张图：

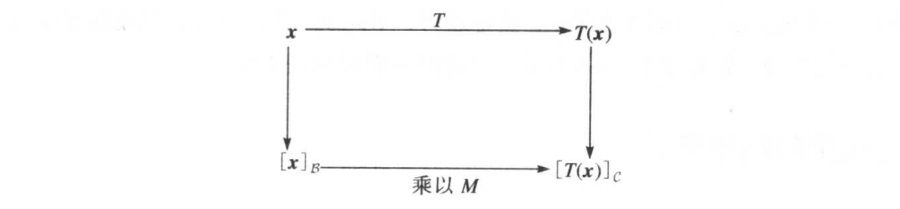
矩阵M是T的矩阵表示，称为T相对于基B和C的矩阵。就坐标向量而言，T对x的作用相当于用矩阵M左乘x。
V到V的线性变化
我们来看看基不变的情况，这时V=W，C=B，M就叫做T的B-矩阵，也就有
$[T(x)]_B=[T]_B[x]_B$
这里我们就是选定了B这组基(●'◡'●)嗯。
矩阵表示的相似性
如果$A=PCP^{-1}$，即A相似于C，若$\mathbb{R}^n$的基B由P的列向量组成，那么C是变换x->Ax的B-矩阵。

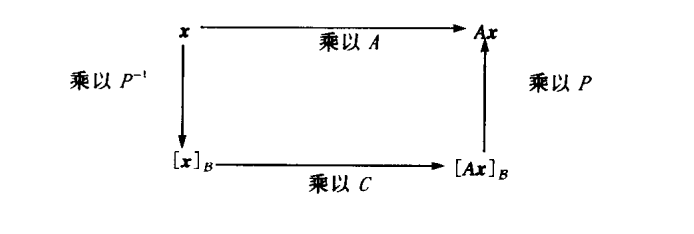
5.5 复特征值*

通过复数的拓展，可以把之前的结论进行推广，开辟新领域，但是我觉得还是看看就好，用到之前没有太大必要深究。
注意一个，一般矩阵如果有复特征值/特征向量，特征值/向量往往是共轭的。即，a+bi和a-bi都是特征。

5.6 离散动力系统* 5.7微分方程中应用 *

注意几个概念
1. 吸引子 对于动力系统$x_{k+1}=Ax_k$，所有轨迹趋向的点。
2. 鞍点 对于动力系统$x_{k+1}=Ax_k$，在某些方向上吸引解，其他方向上又排斥解的点。
3. 基础解系 微分方程$x'=Ax$一定存在含有n个线性无关函数的基础解集，使得每一个解都可以唯一地表示为这n个函数的线性组合。
4. 解耦 仅依赖于元素自身，而不依赖于各元素的组合。 例如函数的导数。

5.8 特征值的迭代估计*

因为在实际应用中，很难能精确得到特征值，但是幸运的是，一个较精确的近似值就可以达到满意的效果。
幂算法 适用于求矩阵A的主特征值（绝对值最大的特征值）

1. 选择一个最大分量为1的初始向量$x_o$
2. 对$k=0,1,..$
   
   • a. 计算$Ax_k$
   • b. 设$\mu_k$是$Ax_k$中绝对值最大的分量
   • c. 计算$x_{k+1}=(1/\mu_k)Ax_k$
3. 几乎对所有选择的$x_0$，序列{$\mu_k$}都近似于主特征值，而序列{$x_k$}近似于对应的特征向量

逆幂法 已知特征值的初步估计后用以对任一特征值近似估值。

错题

补充习题

• 1.l 判断：矩阵A的两个特征向量之和仍是A的特征向量

  正解：错，只有两个对应于同一个特征值的特征向量的和才是。题目没看清就做了QAQ

• 1.v 判断：矩阵A，B均为N维可逆矩阵，则AB相似于BA

  正解：对，因为存在$P=A^{-1}$使$AB=P(AB)P^{-1}$

• 9 证明：当A的所有特征值都小于1时，I-A可逆。

  正解： 反证法， 假设I-A不可逆
  那么$(I-A)x=0$有非零解，则有$Ax=1x$，则有特征值为1，与题设矛盾，所以I-A一定可逆。

心得拾遗

1. 首先注意啦，相似性和行等价是完全不同的两回事，对矩阵做行变换通常会改变特征值。
2. 注意甄别5.4中线性变换和4.7基变换的区别和联系。当5.4中B和C是同一空间V的基时，M就相当于4.7中坐标变换矩阵。Tips线性变换中注意①向量空间是否变化②向量空间是否是欧几里得空间（$\mathbb{R}^n$）③基是否变化
3. 其实5.4这里有点不理解，为啥要把基变换和线性变换搅和到一起去呢？分别来算不是很清楚吗?
   Update： 之前竟然没有认识到编者的用心，其实基变换和线性变换可以说是同源的。对于线性变换，我们可以用矩阵来表示，对向量b实施变换A，就用A乘b，得变换后为Ab。当$A^{-1}$各列线性无关时，$A^{-1}$可以表示一组基，那么将单位基度量的b转换到以$A^{-1}$为基的坐标系中，用的操作也是左乘，即Ab就是b在新坐标系中的坐标。这里，变换是相对的，本质上讲，基变换和线性变换是一样的操作。那么不难发现，所谓的相似矩阵的真相是若两个矩阵相似，那么它们可能是同一个对象在不同坐标系中的描述。这里的对象可以是线性变换（矩阵本身表示变换），也可以是向量的组合（不是向量的集合，因为集合内对象无序）。
4. 一个常见的误区就是，对特征向量的理解，我们平常所见的“求特征向量”，其实是求特征值对应的特征空间的基。特征空间里所有向量都是特征向量，对应每个特征值的特征向量都是无穷的，所以我们要求的是特征空间的基，有了基，只要随便搞搞基搞个基的线性组合，就都是该特征值对应的特征向量。 注意，不同特征值对应的特征向量的线性组合可不是特征向量。
5. 插播一个习题中的概念和结论，5.4的习题中提到矩阵的迹，记作tr(A)，它表示矩阵主对角线元素之和，可以证明，矩阵的迹等于其特征值之和。$tr(A)=\sum\{\lambda|Ax=\lambda x\}$