HiHo一下 Week7 完全背包

HiHo

题目描述

小Ho现在手上有M张奖券，而奖品区有N种奖品，分别标号为1到N，其中第i种奖品需要need(i)张奖券进行兑换，并且可以兑换无数次，为了使得辛苦得到的奖券不白白浪费，小Ho给每件奖品都评了分，其中第i件奖品的评分值为value(i),表示他对这件奖品的喜好值。现在他想知道，凭借他手上的这些奖券，可以换到哪些奖品，使得这些奖品的喜好值之和能够最大。

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第一行为两个正整数N和M,表示奖品的种数，以及小Ho手中的奖券数。

接下来的n行描述每一行描述一种奖品，其中第i行为两个整数need(i)和value(i)，意义如前文所述。

测试数据保证

对于100%的数据，N的值不超过500，M的值不超过10^5

对于100%的数据，need(i)不超过2*10^5, value(i)不超过10^3

输出

对于每组测试数据，输出一个整数Ans，表示小Ho可以获得的总喜好值。

样例输入

5 1000
144 990
487 436
210 673
567 58
1056 897

样例输出

    5940

思路

01背包的变种，完全背包。01背包之所以叫01背包是因为每种物品有0状态-不放进背包和1状态-放进背包。完全背包除了放和不放还要考虑放几个的问题。解决这个问题有个很简单的拆分法，即把同样的物品看成k中不同的物品(但是value和need相同),k即为空背包中能够放的该物品的最大数量。这样就可以把完全背包转化为01背包来做了，这种化归的思想很重要，但是这样的缺点是会导致最高常数级的复杂度提升。
经过思考，我们可以发现的是当你在考虑是否放这类物品的第k件时，需要用到的信息中部分是在考虑是否放k-1件时已经处理过的。假设ans[j]表示负载为j时的最大价值，我们在考虑第k件在负载为j时是否应该放这一件，那么处理上一件时得到的信息ans[j-need]就可以用上了。
状态转移方程依然没变：
ans[j]=max(ans[j],ans[j-need+value)
这里用了空间优化，所以只开了一维数组(因为考虑第i类物品的时候,只需要第i-1类处理完得到的信息，而第i类物品处理完之后可以直接覆盖上去)。
但是需要注意的是因为因为可以放多件物品了，所以在遍历背包容量的时候，我们要正向遍历，即从0~m，而不是从m~need这样递减遍历。如下图

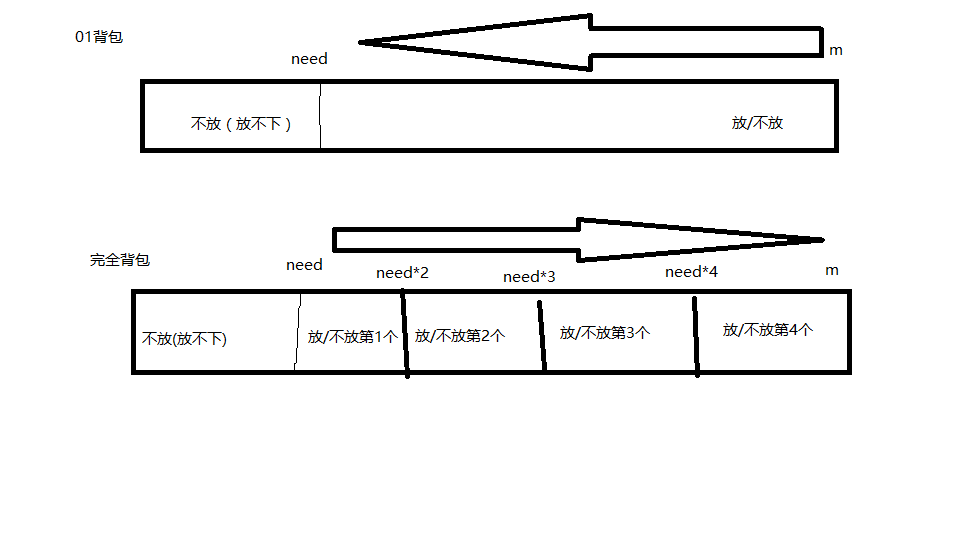
代码

相比上一题代码只需要改动两行

#include<iostream> 
using namespace std;
using namespace std;
int max(int a,int b){
    if(a>b) return a;
    else return b;
}
int main()
{
    int n,m,i,j;
    int need;
    int value;
    int ans[100002]={0};
    cin >> n >>m;
    for (i=0;i<n;i++){
    cin >> need>>value;
    //只需要改动下面两行
    for(int j=need;j<=m;j++)
        ans[j]= max(ans[j],ans[j-need]+value);
    }
        cout <<ans[m];  
    return 0;
}