求职GO：OpenGL与OpenGL-ES面试大全(持续更新)

面试题 0

版本：0
作者：陈小默
声明：禁止商业，禁止转载

一、基本概念

1.1 名词解释

• 图元：
• 凸多边形(convex polygon)：凸多边形满足以下特点：
  
  • 1，所有内角小于180°；
  • 2，内部所有点仅在任意一边延长线的一侧；
  • 3，内部任意两点的连线也在内部。
• 退化多边形(degenerate polygon)：存在共线或者重叠坐标和线段的多边形。
• 图形对象/标准图形对象(graphics object/standard graphics object)：使用一组多边形片面描述的对象。
• 填充区(fill area)：使用某种颜色或图案进行填充的区域。
• 片元：
• 凹多边形(concave polygon)：不是凸多边形的多边形。
• 深度测试：
• 多边形(polygon)：任意有封闭折线边界的平面。
• GPU：
• 光栅化：
• 光栅化单元(rasterizer)：光栅化单元负责对所有的剪切区域内的图元生成片元数据，然后堆每一个生成的片元都执行一个片元着色器。
• 帧缓存：
• 着色器：
• 着色管线装配(shader plumbing)：将应用程序数据与着色器程序的变量关联起来。
• 渲染(render)：表示计算机从模型创建最终图像的过程。
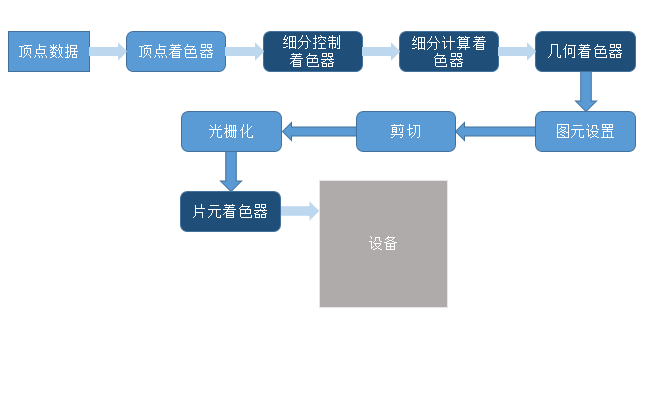
• 渲染管线(rendering pipeline)：它是一系列数据处理过程，并且将应用程序的数据转换到最终渲染的图像。OpenGL首先接收用户提供的几何数据(顶点或几何图元)，并且将他输入到一系列着色器阶段中进行处理，包括：顶点着色、细分着色，以及最后的几何着色，然后它将被送入光栅化单元。
• 像素(pixel)：显示设备上的最小可见单位。
• 裁剪空间：
• 标准多边形(standard polygon)：不存在边界重叠交叉的多边形。
• 模版测试：
• 模型/场景对象：

1.2 简述OpenGL渲染管线过程

• 1、准备向OpenGL传输数据
  OpenGL需要将所有的数据都保存到缓存对象(buffer object)中，它相当于OpenGL服务端维护的一块内存区域。
• 2、将数据传输到OpenGL
  在缓存初始化完成之后，通过调用绘制命令将顶点数据传送到OpenGL服务端。我们可以将一个顶点视为一个需要统一处理的数据包。这个包中的数据可以是我们需要的任何数据。
• 3、顶点着色(vertex shading stage)
  该阶段将接收你顶点缓存中给出的顶点数据。对于绘制命令传输的每个点，OpenGL都会用一个顶点着色器来处理顶点相关的数据(至少会计算出每个顶点经过建模和观察投影变换后在裁剪空间的坐标)。传递着色器会将数据复制并传递到下一个着色阶段。对于复杂的场景也会有相应的着色方式。
• 4、细分着色(tessellation shading stage)
  这是一个可选阶段，与应用程序中显式地指定几何图元的方法不同，它会在OpenGL管线内部生成新的几何体。这个阶段启用之后，会收到来自顶点着色器阶段的输出数据，并且对收到的数据进一步处理。
• 5、 几何着色(geometry shading stage)
  该阶段也是一个可选阶段，假如启用了该阶段，它会收到来自顶点着色或者细分着色(如果它也被启用)的数据，然后在OpenGL管线内部对几乎所有的几何图形进行修改。几何着色器不同于前两个着色器，它不仅仅只能修改输入数据，甚至可以创建新的图元交给后续的流水线处理。该阶段作用于每个独立的几何图元。
• 6、图元装配
  该阶段会将这些顶点与相关的集合图元之间组织起来，准备下一步的剪切和光栅化工作。
• 7、剪切
  该阶段用来保证相关的像素不会在窗口之外进行绘制。也就是说将不能被窗口显示的部分去除。
• 8、光栅化
  图元信息最终被传递给光栅化单元，生成对应的片元。
• 9、片元着色(fragment shading stage)
  这是最后一个可以通过编程控制屏幕显示颜色的阶段。在这个阶段中会使用着色器来计算片元的最终颜色和它的深度值。(顶点着色决定了一个图元应该处于屏幕的什么位置，片元着色决定了某个片元的颜色应该是什么)。
• 10、片元操作
  在该阶段会使用深度测试和模版测试的方式来决定一个片元是否是可见的。如果一个片元成功的通过了所有激活的测试，那么他就可以直接被绘制到帧缓存中了，它所对应的像素的颜色值会被更新，如果开启了融合模式，那么对应的片元颜色会与该像素的颜色相叠加，形成一个新的颜色并写入帧缓存中。

1.3 简述着色器的使用流程

整个着色器的使用流程如下：

• 1，创建着色器对象
• 2，把源码关联到每个着色器对象
• 3，编译着色器
• 4，创建程序
• 5，关联着色器到程序对象
• 6，链接程序
• 7，激活和关闭着色器程序
• 8，删除着色器和程序

更多详细信息请参考OpenGL——使用着色器

1.4 如何使用日志输出着色器错误

OpenGL中提供了日志系统，我们只需要查询日志系统，就可以的到相应的错误信息。对于日志，我们需要查询到日志的长度，然后将日志读到一个字符缓冲区再输出。下面的例子实现了这个过程

    GLint length;
    GLsizei num;
    GLchar *log;
    glGetProgramiv(program,GL_INFO_LOG_LENGTH,&length);
    if(length>0){
        log = (GLchar *)malloc(sizeof(GLchar)*length);
        glGetProgramInfoLog(program,length,&num,log);
        println(log);
        free(log);
    }

1.5 GL_LINES、GL_LINE_STRIP 和 GL_LINE_LOOP有什么区别？

• GL_LINES：可以连接每一对相邻点而得到一组直线。如果最后一个端点处于奇数位置，则该点会被忽略。
• GL_LINE_STRIP：会将传入的点依次连接直到最后一个端点。
• GL_LINE_LOOP：在GL_LINE_STRIP的基础上又进行了首尾相连。

1.6 GL_TRIANGLES、GL_TRIANGLE_STRIP 和 GL_TRIANGLE_FAN有什么区别？

• GL_TRIANGLES：会将矩阵中每三个点取出绘制一个三角形，最后一组不足三个则自动忽略；
• GL_TRIANGLE_STRIP：绘制时满足以下规则：第n(奇数,从1到k)个三角形将会连接n,n+1,n+2三个顶点，对于第n(偶数)个三角形将会连接n+1,n,n+2三个顶点。所以总共会绘制k-2个三角形。
• GL_TRIANGLE_FAN：绘制时满足以下规则：第n(从1到k)个三角形将会连接1,n+1,n+2三个顶点。总共会绘制k-2个三角形。

1.7 GL_QUADS 和 GL_QUAD_STRIP有什么区别？

• GL_QUADS：每四个点绘制一个四边形，最后一组不足四个则忽略。
• GL_QUAD_STRIP：在第n(1..k)个四边形中，奇数满足(2n-1,2n,2n+2,2n+1),偶数满足(2n,2n-1,2n+2,2n-1)。

二、设计思想

三、图像算法

3.1 贝塞尔曲线专题

贝塞尔曲线是依据任意位置的点坐标绘制出的一条光滑曲线。其设计思路是按照规律u从0到1的移动过程中，在各个控制点连线的相应位置取点，并对相邻两条线上的点再次连线，重复以上过程使得没有可连接的两个点。
详细内容请参考图形算法：贝塞尔曲线。

3.2 如何识别凹多边形

凹多边形中至少有一个内角大于180°。凹多边形会有至少一条边的延长线与其他边相交，有时一对内点的连线会与会与多边形边界相交。我们可以根据里的任意一个特征识别凹多边形。

• 向量法：我们按照同方向为每一条边做一个向量，然后分别计算相邻两个向量的叉积，凸多边形的所有相邻向量叉积的$z$分量均同号，对于正负同时存在的情况，则可确定为凹多边形。
• 观察法：我们可以观察多边形的每一条边的延长线与其他顶点的关系。如果某些顶点在延长线的一侧，而有一些在另一侧，则可以确定为凹多边形。

3.3 如何分割凹多边形

3.4 简述什么是内-外测试

当我们需要对一个图形进行处理的时候通常需要区分图形的内外区域。对于简单图形的内外识别通常是一件很简单的事，但是对于比较复杂的图形，我们可以采用下面两种常见的方法。

• 奇偶规则(odd-even rule)：在任意位置$P$到无限远处做一条射线，统计这条射线穿过的边界数量。如果是奇数表示点$P$所在的位置是图形内部，否则是外部。
• 非零环绕数规则(nonzero winding-number)：以逆时针作为旋转方向为每一条边界做一条向量。在任意位置$P$到无限远处做一条射线。在这条射线与边界交叉时根据向量从左到右穿过射线为-1，反之为1，然后统计所有交叉处的和。当和为0时表示当前点所在的位置是外部，否则是内部。

3.5 如何进行图形的交、并、差运算

非零环绕数规则可以用来计算两个图形交、并、差运算

• 交集：对两个图形都采用逆时针的环绕方向，然后进行非零环绕计算，所有结果大于1的点所在的集合就是两个图形的交集。
• 并集：对两个图形都采用逆时针的环绕方向，然后进行非零环绕计算，所有非零点的集合就是两个图形的并集。
• 差集：假设有图形A和B，计算A-B的差，我们可以取A为逆时针环绕，取B为顺时针环绕，然后进行非零环绕计算，所有非零点的集合就是A与B的差。

3.6 如何判断前向面与后向面

通常情况下我们通过图形顶点的旋转方向来区分前向面与后向面，在此之前我们需要指定前向面的旋转方向。那么我们应该如何判断一个点之于一个面的关系呢？这里我们用到了平面方程

$$Ax+By+Cz+D=0$$ 我们可以逆时针选取凸多边形的三个连续顶点$(x_1,y_1,z_1)$，$(x_2,y_2,z_2)$，$(x_3,y_3,z_3)$，联立求解上述方程，可以得到求得系数
$$A=\begin{vmatrix} 1 & y_1 & z_1 \\ 1 & y_2 & z_2 \\ 1 & y_3 & z_3 \\ \end{vmatrix} B=\begin{vmatrix} x_1 & 1 & z_1 \\ x_2 & 1 & z_2 \\ x_3 & 1 & z_3 \\ \end{vmatrix} \\ C=\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{vmatrix} D=-\begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{vmatrix}$$
对于判断控件中任意一点$(x,y,z)$与该平面的关系，只要将点的坐标带入上述方程即可:
如果$Ax+By+Cz+D=0$则该点在平面上
如果$Ax+By+Cz+D \lt 0$则该点在平面后方
如果$Ax+By+Cz+D\gt 0$则该点在平面前方
上述测试在右手笛卡尔坐标系中有效，多边形表面的方向可由笛卡尔法向量$(A,B,C)$表示。

四、程序设计

五、OpenGL-ES 3.0 面试大全

5.1 NDK for Android

5.2 SDK for Android