图形算法：直线算法

算法

版本：3
作者：陈小默
声明：禁止商用，禁止转载

发布于：作业部落、CSDN博客

---

场景中的直线由其两端点的坐标位置来定义。要在光栅监视器中显示一条线段，图形系统必须先将两端点投影到整数屏幕坐标，并确定离两端点间的直线路径最近的像素位置。接下来才是将颜色填充到相应的像素坐标。[1]

前言

---

文章最后的演示代码使用的是C++语言，函数库使用的是以GLUT为基础的自定义封装库。本章内容将介绍生成直线的直线方程算法、DDA算法以及重要的Bresenham算法。

一、算法导论

以下仅仅展示算法的计算过程，具体实施请参考示例程序部分。

---

1.1直线方程算法

对于绘制直线来说，使用直线方程无疑是一种最直接的算法。在二维笛卡尔坐标系中，直线方程为：

$$y=m*x+b \tag{1.1}\label{1.1}$$
其中m代表直线的斜率，b为直线的截距，对于任意两个端点$(x_0,y_0)$和$(x_1,y_1)$：
$$m=\frac{y_1-y_0}{x_1-x_0}\tag{1.2}$$
$$b=y_0-m*x_0\tag{1.3}$$
由于屏幕上的点在其坐标系中以整数表示，当斜率 $1>|m|$ 时，我们可以以 $x$ 轴增量 $\delta x$ 计算相应的y轴增量 $\delta y$：
$$\delta y=m*\delta x\tag{1.4}\label{1.4}$$
同样，对于斜率 $|m|>1$ 的线段，我们需要通过以 $y$ 轴增量 $\delta y$ 计算相应的 $x$ 轴增量 $\delta x$ ：

$$\delta x=\frac{\delta y}{m} \tag{1.5}\label{1.5}$$

通过使用直线方程绘制的点，其优点是算法简单且精确，但是其在绘制每一个点的过程中都需要计算一次乘法和加法，显而易见，由于乘法的存在，导致运算时间大幅度增加。接下来介绍的DDA算法将弥补直线方程的乘法缺陷。

1.2 DDA算法

从上可知，在绘制大量点的过程中，我们要尽可能的减少每一个点的计算时间。在计算机中加法运算是最简单的运算之一了。我们可以利用直线的微分特性将每一步的乘法运算替换为加法运算。数字微分分析法(Digital Differential Analyzer，DDA)是一种线段扫描转换算法，基于式 $\eqref{1.4}$ 或 $\eqref{1.5}$ 来计算 $\delta x$ 或 $\delta y$。

对于斜率 $|m| \le 1$ 的线段来说，我们仍以单位 $x$ $(\delta x = 1)$ 间隔(考虑到屏幕设备坐标为连续整数)取样，并逐个计算每一个 $y$ 值。

$$y_{k+1}=y_k+m \tag{1.6}\label{1.6}$$

于是，我们便将乘法运算合理的转换为了加法运算。但是需要注意的是，在屏幕设备中的坐标均是整数，所以我们在绘制时的y需要取整。
对于具有大于1的正斜率线段，则需要交换 $x$ 和 $y$ 的位置。也就是以单位 $y$ 间隔 $(\delta y=1)$取样，顺序计算每一个 $x$ 的值

$$x_{k+1}=x_k+\frac{1}{m} \tag{1.7}\label{1.7}$$

此时，每一个计算出的 $x$ 要沿着 $y$ 扫描线舍入到最近的像素位置。

该算法只需要计算出一个 $step$ 值( $m$ 或者 $\frac{1}{m}$ )，然后就可以沿着路径的方向计算出下一位像素。然而，该算法的缺点显而易见，在数学上，该算法能够保证计算结果准确无误，但是，由于计算机中的数据类型具有精度限制，这将会导致大量数据处理的误差积累。并且，其虽然消除了直线方程中的乘法运算，但是对于浮点数的运算和取整仍然十分耗时。

1.3 Bresenham算法

---

接下来我们介绍由布莱森汉姆(Bresenham)提出的精确且高效的光栅线生成算法，该算法仅仅使用整数增量计算，除此之外，该算法还能应用于圆或者其他曲线。

我们将分别介绍四种斜率($m \gt 1$ 、 $0 \lt m \lt 1$ 、 $-1 \lt m \lt 0$ 和 $m \lt -1$)的计算过程(以下示例均为从左至右画线)。

1.3.1 斜率大于1

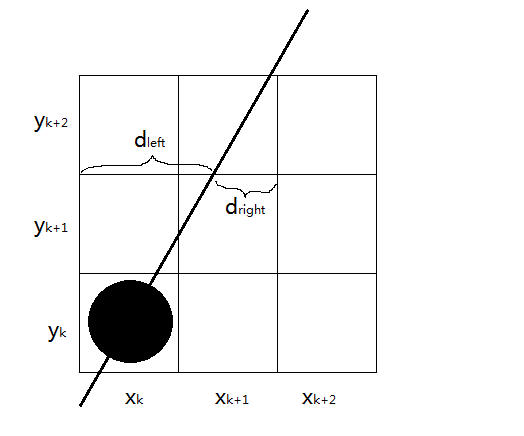
首先，在斜率大于1的情况下，沿路径像素以单位 $y$ 间隔取样。假设线段以$(x_0,y_0)$开始对于其路径上已绘制的$(x_k,y_k)$点我们需要判定下一个点的绘制位置是$(x_{k+1},y_{k+1})$还是$(x_k,y_{k+1})$。

在取样位置 $y_{k+1}$ 我们使用 $d_{left}$ 和 $d_{right}$ 来标识两个像素位置($x_k$与$x_{k+1}$)与数学位置的水平偏移量。根据式 $\eqref{1.1}$ 可得在像素列 $y_{k+1}$ 处的 $x$坐标计算值为

$$x=\frac{(y_{k+1}-b)}{m}=\frac{(y_k+1-b)}{m} \tag{1.8}\label{1.8}$$

所以

$$d_{left}=x-x_k=\frac{y_k+1-b}{m}-x_k \tag{1.9}\label{1.9}$$

且

$$d_{right}=x_{k+1}-x=x_k+1-\frac{y_k+1-b}{m} \tag{1.10}\label{1.10}$$

为了确定两个像素中哪一个更接近真实路径，需要计算两个像素偏移的差值。

$$d_{left}-d_{right}=2\frac{y_k+1-b}{m}-2x_k-1 \tag{1.11}\label{1.11}$$

设线段终点位置为$(x_1,y_1)$，可得

$$m=\frac{\Delta y}{\Delta x}=\frac{y_1-y_0}{x_1-x_0} \tag{1.12}\label{1.12}$$

设决策参数 $p_k=\Delta y(d_{left}-d_{right})$

$$p_k=2\Delta xy_k-2\Delta yx_k+C \tag{1.13}\label{1.13}$$

其中

$$C=2\Delta x(1-b)-\Delta y \tag{1.14}\label{1.14}$$

在第 $k+1$ 步，决策参数可以由式$\eqref{1.13}$计算得出

$$p_{k+1}=2\Delta x(y_k+1)-2\Delta yx_{k+1}+C \tag{1.15}\label{1.15}$$

将上述等式减去式$\eqref{1.13}$可得决策值的增量$\delta p_{k+1}$

$$\delta p_{k+1}=p_{k+1}-p_k=2\Delta x-2\Delta y(x_{k+1}-x_k) \tag{1.16}$$

其中$x_{k+1}-x_k$的取值可能为0，也可能为1，这由前一个决策值$p_k$的正负决定，也就是说如果$p_k\lt 0$，则下一个绘制的点是$(x_k,y_{k+1})$ 否则绘制$(x_{k+1},y_{k+1})$。并且绘制的点的位置又决定了该位置的决策值大小。

目前我们有了决策值之间的增量关系，仅需求出第一个决策值$p_0$即可，由式$\eqref{1.12}$、式$\eqref{1.13}$、式$\eqref{1.1}$和式$\eqref{1.14}$联立可得

$$p_0=2\Delta x-\Delta y \tag{1.17}$$

绘制过程解析：由于$\Delta y \gt 0$ 所以当$d_{left} \gt d_{right}$时(此时$p_k \gt 0$)， 代表当前数学点更接近与$x_{k+1}$否则更接近与$x_k$。我们仅仅需要求出第一个决策值 $p_0$ 其后的决策值都是前一个决策值与决策增量$\delta p_{k+1}$的和。我们可以在沿线路径的每一个 $x_k$ 处，进行下列检测：

如果 $p_k \lt 0$ 下一个要绘制的点是 $(x_k,y_{k+1})$ ，并且 $p_{k+1}=p_k+2\Delta y$
否则，下一个要绘制的点是 $(x_{k+1},y_{k+1})$ ，并且 $p_{k+1}=p_k+2\Delta y -2\Delta x$

1.3.2 斜率大于0小于1

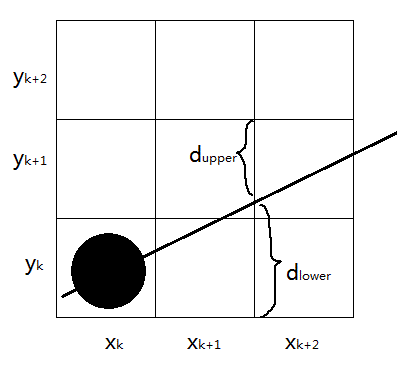
在斜率大于0小于1的情况下，沿路径像素以单位 $x$ 间隔取样。假设线段以$(x_0,y_0)$开始对于其路径上已绘制的$(x_k,y_k)$点我们需要判定下一个点的绘制位置是$(x_{k+1},y_k)$还是$(x_{k+1},y_{k+1})$。

在取样位置 $x_{k+1}$ 我们使用 $d_{upper}$ 和 $d_{lower}$ 来标识两个像素位置($y_k$与$y_{k+1}$)与数学位置的水平偏移量。根据式 $\eqref{1.1}$ 可得在像素列 $x_{k+1}$ 处的 $y$坐标计算值为

$$y=m(x_k+1)+b \tag{1.19}$$

所以

$$d_{lower}=y-y_k=m(x_k+1)+b-y_k \tag{1.20}$$

且

$$d_{upper}=y_{k+1}-y=y_k+1-m(x_k+1)-b \tag{1.21}$$

为了确定两个像素中哪一个更接近真实路径，需要计算两个像素偏移的差值。

$$d_{lower}-d_{upper}=2m(x_k+1)-2y_k+2b-1 \tag{1.22}$$

设决策参数 $p_k=\Delta x(d_{lower}-d_{upper})$

$$p_k=2\Delta yx_k-2\Delta xy_k+C \tag{1.23}\label{1.23}$$

其中

$$C=2\Delta y+\Delta x(2b-1) \tag{1.24}\label{1.24}$$

在第 $k+1$ 步，决策参数可以由式$\eqref{1.23}$计算得出

$$p_{k+1}=2\Delta y(x_k+1)-2\Delta xy_{k+1}+C \tag{1.25}$$

将上述等式减去式$\eqref{1.23}$可得决策值的增量$\delta p_{k+1}$

$$\delta p_{k+1}=p_{k+1}-p_k=2\Delta y-2\Delta x(y_{k+1}-y_k) \tag{1.26}$$

由式$\eqref{1.12}$、式$\eqref{1.23}$、式$\eqref{1.1}$和式$\eqref{1.24}$联立可得第一个决策值$p_0$

$$p_0=2\Delta y-\Delta x \tag{1.27}$$

1.3.3 斜率大于-1小于0

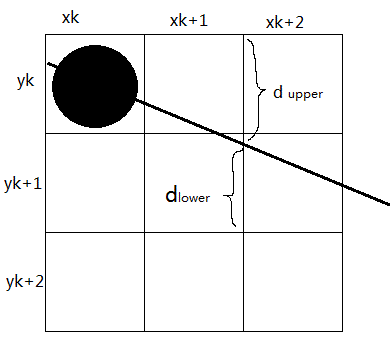
在斜率大于-1小于0的情况下，沿路径像素以单位 $x$ 间隔取样。假设线段以$(x_0,y_0)$开始对于其路径上已绘制的$(x_k,y_k)$点我们需要判定下一个点的绘制位置是$(x_{k+1},y_k)$还是$(x_{k+1},y_{k+1})$。

在取样位置 $x_{k+1}$ 我们使用 $d_{upper}$ 和 $d_{lower}$ 来标识两个像素位置($y_k$与$y_{k+1}$)与数学位置的水平偏移量。

$$d_{lower}=y-y_{k+1}=m(x_k+1)+b-(y_k-1) \tag{1.28}$$

且

$$d_{upper}=y_k-y=y_k-m(x_k+1)-b \tag{1.29}$$

为了确定两个像素中哪一个更接近真实路径，需要计算两个像素偏移的差值。

$$d_{upper}-d_{lower}=2y_k-2m(x_k+1)-2b-1 \tag{1.30}\label{1.30}$$

设决策参数 $p_k=\Delta x(d_{upper}-d_{lower})$

$$p_k=2\Delta xy_k-2\Delta yx_k+C \tag{1.31}\label{1.31}$$

其中

$$C=-2\Delta y-\Delta x(2b-1) \tag{1.32}\label{1.32}$$

在第 $k+1$ 步，决策参数可以由式$\eqref{1.31}$计算得出

$$p_{k+1}=2\Delta xy_{k+1}-2\Delta y(x_k+1)+C \tag{1.33}$$

将上述等式减去式$\eqref{1.32}$可得决策值的增量$\delta p_{k+1}$

$$\delta p_{k+1}=p_{k+1}-p_k=2\Delta x(y_{k+1}-y_k)-2\Delta y \tag{1.34}$$

由式$\eqref{1.12}$、式$\eqref{1.30}$、式$\eqref{1.1}$和式$\eqref{1.31}$联立可得第一个决策值$p_0$

$$p_0=\Delta x-2\Delta y \tag{1.35}$$

1.3.4 斜率小于-1

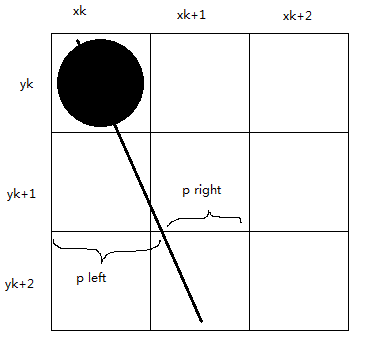
在斜率小于-1的情况下，沿路径像素以单位 $y$ 间隔取样。假设线段以$(x_0,y_0)$开始对于其路径上已绘制的$(x_k,y_k)$点我们需要判定下一个点的绘制位置是$(x_{k+1},y_{k+1})$还是$(x_k,y_{k+1})$。

在取样位置 $y_{k+1}$ 我们使用 $d_{left}$ 和 $d_{right}$ 来标识两个像素位置($x_k$与$x_{k+1}$)与数学位置的水平偏移量。根据式 $\eqref{1.1}$ 可得在像素列 $y_{k+1}$ 处的 $x$坐标计算值为

$$x=\frac{(y_{k+1}-b)}{m}=\frac{(y_k-1-b)}{m} \tag{1.36}$$

所以

$$d_{left}=x-x_k=\frac{y_k-1-b}{m}-x_k \tag{1.37}$$

且

$$d_{right}=x_{k+1}-x=x_k+1-\frac{y_k-1-b}{m} \tag{1.38}$$

为了确定两个像素中哪一个更接近真实路径，需要计算两个像素偏移的差值。

$$d_{left}-d_{right}=2\frac{y_k-1-b}{m}-2x_k-1 \tag{1.39}$$

设线段终点位置为$(x_1,y_1)$，可得

$$m=\frac{\Delta y}{\Delta x}=\frac{y_1-y_0}{x_1-x_0} \tag{1.40}$$

设决策参数 $p_k=\Delta y(d_{right}-d_{left})$(在从左到右的绘制过程中$\Delta y \lt 0$ 为了保持符号统一，所以交换$d_{left}$和$d_{right}$位置)

$$p_k=-2\Delta xy_k+2\Delta yx_k+C \tag{1.41}\label{1.41}$$

其中

$$C=2\Delta x(1+b)+\Delta y \tag{1.42}$$

在第 $k+1$ 步

$$p_{k+1}=-2\Delta x(y_k-1)+2\Delta yx_{k+1}+C \tag{1.43}$$

将上述等式减去式$\eqref{1.41}$可得决策值的增量$\delta p_{k+1}$

$$\delta p_{k+1}=p_{k+1}-p_k=2\Delta x+2\Delta y(x_{k+1}-x_k) \tag{1.44}$$

目前我们有了决策值之间的增量关系，仅第一个决策值$p_0$

$$p_0=2\Delta x+\Delta y \tag{1.45}$$

二、程序演示

---

在上面得的算法分析中，我们已经了解了三种算法的基本思想与设计思路。这里通过C++程序演示其过程(也可以通过其他图形软件包比如Java的swing或者Android的Canvas实现)，实现方式各异，不必拘泥于细节。

首先定义一个显示用来显示图形的View

#ifndef lineview_h
#define lienview_h
#include"cxm.h"
class LineView:public View{
private:
    _Paint _paint;//画笔指针
    _StringArray _names;//字符串数组指针
    List<IntArray> *_arrays;//存放了整型数组的链表对象，数组中为计算出的点的坐标位置
public:
    int bottom,top;
    LineView();
    ~LineView();
    void LineEquation(double x1,double y1,double x2,double y2);//使用直线方程画线
    void DDA(double x1,double y1,double x2,double y2);//使用DDA算法画线
    void Bresenham(double x1,double y1,double x2,double y2);//布莱森汉姆算法
    virtual void onDraw(Canvas &canvas);//图案绘制方法
};
typedef LineView* _LineView;
typedef LineView& LineView_;
#endif

接下来实现其中的构造与析构函数

LineView::LineView(){
    _paint = new Paint;
    _names = new StringArray(4);
    _arrays = new LinkedList<IntArray>;
    StringArray_ names_=*_names;
    names_[0]="OpenGL";
    names_[1]="Equation";
    names_[2]="DDA";
    names_[3]="Bresenhan";
}
LineView::~LineView(){
    delete _paint;
    delete _names;
    delete _arrays;
}

接下来我们实现使用直线方程的方法，该方法将计算出的点保存在了整型数组中，并将数组存储到链表

void LineView::LineEquation(double x1,double y1,double x2,double y2){//y=mx+b
    _IntArray  _arr;
    double dy = y2-y1;
    double dx = x2-x1;
    double m = dy/dx;
    double b = y1 - m*x1;
    if(abs(m)>1){//以y轴像素为单位 x=(y-b)/m
        int size = abs(2*int(dy));//存放坐标的数组长度
        _arr = new IntArray(size);
        IntArray_ arr=*_arr;
        int start = int(y1<y2?y1:y2);//取最小起始位置
        int end = start+abs(int(dy));
        for(int i=start,j=0;i<end;i++){
            arr[j++]=int((i-b)/m);//x坐标
            arr[j++]=i;//y坐标
        }
    }else{//以x轴像素为单位 y=mx+b
        int size = abs(2*int(dx));//存放坐标的数组长度
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int start = int(x1<x2?x1:x2);//取最小起始位置
        int end = start+abs(int(dx));
        for(int i=start,j=0;i<end;i++){
            arr[j++]=i;//x坐标
            arr[j++]=int(b+m*i);//y坐标
        }
    }
    _arrays->add(_arr);
}

然后实现使用DDA画线的算法计算出各点

void LineView::DDA(double x1,double y1,double x2,double y2){
    _IntArray _arr;
    double dy = y2-y1;
    double dx = x2-x1;
    double m = dy/dx;
    if(abs(m)>1){//以单位y取样
        double rate = 1/m;
        int size = abs(2*int(dy));//存放坐标的数组长度
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int start = int(y1<y2?y1:y2);//取最小起始位置
        int end = start+abs(int(dy));
        double rx = y1<y2?x1:x2;
        for(int i=start,j=0;i<end;i++){
            rx+=rate;
            arr[j++]=int(rx);
            arr[j++]=i;
        }
    }else{//以单位x取样
        double rate = m;
        int size = abs(2*int(dx));//存放坐标的数组长度
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        int start = int(x1<x2?x1:x2);//取最小起始位置
        int end = start+abs(int(dx));
        double ry = x1<x2?y1:y2;
        for(int i=start,j=0;i<end;i++){
            ry+=rate;
            arr[j++]=i;
            arr[j++]=int(ry);
        }
    }
    _arrays->add(_arr);
}

最后是Bresenham算法的简单实现

void LineView::Bresenham(double x1,double y1,double x2,double y2){
    _IntArray _arr;
    double dy=y2-y1;
    double dx=x2-x1;
    double m = dy/dx;
    if(m>1){//以单位y取样
        int size = abs(2*int(dy));
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        double p = 2*dx-dy;//po
        double left = 2*dx;
        double right = 2*dx-2*dy;
        int start = int(y1);
        int end = start+abs(int(dy));
        int x = int(x1);
        for(int y=start,i=0;y<=end;y++){
            if(p<0){
                arr[i++]=x;
                p+=left;
            }else{
                arr[i++]=++x;
                p+=right;
            }
            arr[i++]=y;
        }
    }else if(m>0&&m<1){//以单位x取样
        int size = abs(2*int(dx));
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        double p = 2*dy-dx;
        double upper = 2*dy;
        double lower = 2*dy-2*dx;
        int start = int(x1);
        int end = start + abs(int(dx));
        int y = int(y1);
        for(int x=start,i=0;x<=end;x++){
            arr[i++]=x;
            if(p<0){
                arr[i++]=y;
                p+=upper;
            }else{
                arr[i++]=++y;
                p+=lower;
            }
        }
    }else if(m<0&&m>-1){//以单位x取样
        int size = abs(2*int(dx));
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        double p = dx-2*dy;
        double upper = -2*dy;
        double lower = -2*dx-2*dy;
        int start = int(x1);
        int end = start + abs(int(dx));
        int y = int(y1);
        for(int x=start,i=0;x<=end;x++){
            arr[i++]=x;
            if(p<0){
                arr[i++]=y;
                p+=upper;
            }else{
                arr[i++]=--y;
                p+=lower;
            }
        }
    }else{//以单位y取样
        int size = abs(2*int(dy));
        _arr = new IntArray(size);
        IntArray_ arr = *_arr;
        double p = 2*dx+dy;
        double left = 2*dx;
        double right = 2*dx+2*dy;
        int start = int(y1);
        int end = start-abs(int(dy));
        int x = int(x1);
        for(int y=start,i=0;y>=end;y--){
            if(p<0){
                arr[i++]=x;
                p+=left;
            }else{
                arr[i++]=++x;
                p+=right;
            }
            arr[i++]=y;
        }
    }
    _arrays->add(_arr);
}

然后在onDraw方法中将所有的点绘制出来

void LineView::onDraw(Canvas &canvas){
    canvas.drawLine(_paint,50,bottom,150,top);
    for(int i=0;i<_arrays->size();i++){
        canvas.drawPoints(*_paint,*(*_arrays)[i]);
    }
    for(int i=0;i<_names->size();i++){
        canvas.drawString(*_paint,i*200+40,25,(*_names)[i]);
    }
}

最后就是在main方法中创建视图窗口，并将刚刚创建的View添加进去

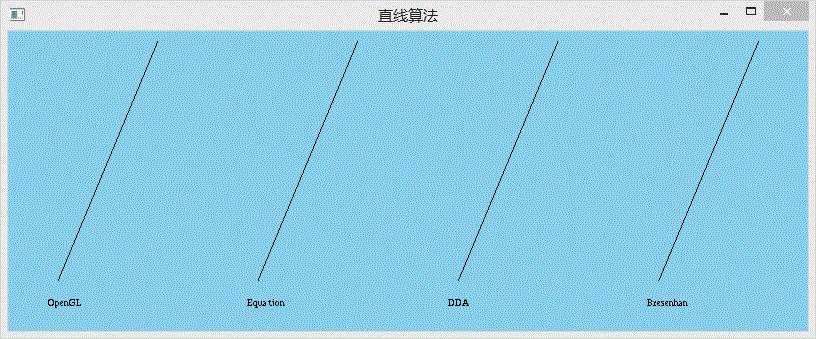
int _tmain(int argc, char* argv[]){
    GlutWindow window(100,300,800,300);
    String title = "直线算法";
    window.setTitle(title);
    window.setBackgroundColor(BLUE_SKY);
    _LineView _view = new LineView();
    LineView_ view=*_view;
    view.bottom=50;
    view.top=290;
    view.LineEquation(250,view.bottom,350,view.top);
    view.DDA(450,view.bottom,550,view.top);
    view.Bresenham(650,view.bottom,750,view.top);
    window.addView(view);
    window.show(&argc,argv);
    return 0;
}

结果图展示