Recomb vs XRTS

XFEL

---

1. Problem Statement

In an XFEL-plasma experiment, a solid density Fe plasma emits photons with energy ~2.5 keV above the XFEL photon energy. The objective is to identify whether this is coming from XRTS or Recombination.

2. Detailed Discription

The emission spectrum of Fe plasma follows:

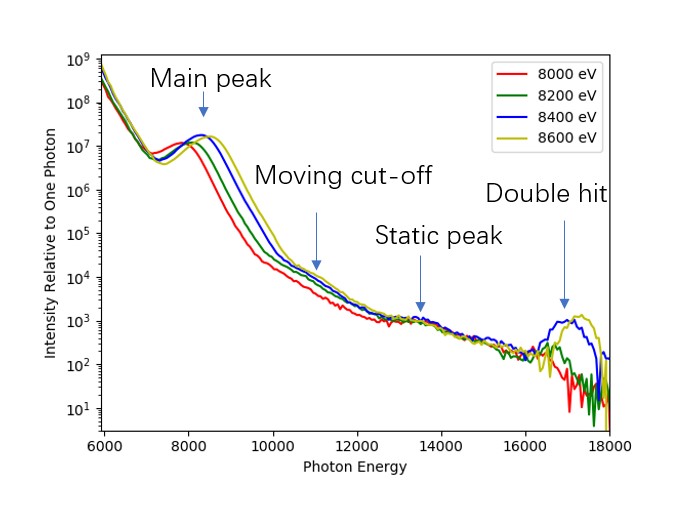
2.1 The Kα peak and the main peak

First, the left-most peak ("main peak") at 8 to 9 keV which moves synchronously with the FEL energy suggests the emission from elastic Thomson scattering on bound electrons. A related question is that if there is any enhancement due to the lattice. To answer this question, we need to look at another figure from Ni Plasma under 9 keV photons:

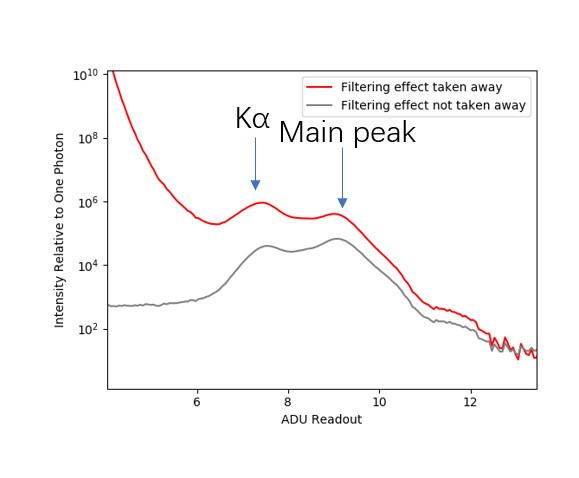
In this run, the FEL photon energy is 9 keV, and thus creates a peak at that energy. Additionally, in this figure, the Kα peak at 7.4 keV is also visible. To see if there is enhancement due to lattice, we can compare the main peak with the Kα peak.

Directly from the figure, the peak (after the filter effect is taken away) at 7.4 keV has about $1\times10^6$ photons. Fitting this as a Gaussian distribution with $\sigma=400~{\rm eV}$ plus a background at about $2\times10^5$ photons, the total number of photons within the $\pm 1 \sigma$ of that peak, excluding the background at $2\times10^5$ is about $8\times10^6$. As the $\pm 1 \sigma$ domain contains roughly 2/3 of the total number in that peak, the total number of photons in K$\alpha$ is $1.2\times10^7$.

The beam energy of a pulse is about $W_{\rm tot}=1.6~{\rm mJ}$, however, only 0.11% of that is received by the target (from the eLog, the transmission is manually set to be $1.1\times 10^{-3}$). The fluorescence yield of K shell is about $\eta=0.4$, therefore, the total number of K$\alpha$ photons emitted to $4\pi$ of the order

$$N_{K_\alpha}=\eta\frac{W_{\rm tot}\times 1.1\times 10^{-3}}{W_{\rm photon}}\approx0.4 \times\frac{1.6~{\rm mJ} \times1.1\times 10^{-3}}{9000~{\rm eV}}\approx5 \times 10 ^{8}.$$ Where $W_{\rm photon}$ is the photon energy of the XFEL. As the detector has $50 \mu {\rm m}$ pixel size and has $704\times 768$ pixels, the total area of the detector is $S=(50~\mu{\rm m})^2 \times 704 \times 768$. Additionally, the distance between the detector and the sample is $r=1.5 {\rm m}$. Hence the solid angle of the detector about: $$\Omega = \frac{S}{r^2} = 6 \times 10 ^{-4},$$ and the number of K$\alpha$ photons at the detector is expected to be of the order:
$$(\Omega / 4\pi) \times N_{K_\alpha} \approx 2.3 \times 10 ^{4}.$$ As each run consists of 342 pluses, the total number of Kα photons recorded on the detector should be the order of $342\times 2.3\times 10^4 \approx 8\times 10^6$, which shows an agreement with the experiment value.

Now it is time to look at the main peak. As the main peak is due to the Thomson scattering from bound electrons, a lattice effect will be observed if we are at a Bragg peak. One way of deciding if there is a lattice effect is to find how photons will be emitted if there is no lattice effect.

Assume that there is no lattice effect. The differential cross section of Thomson scattering is

$$\frac{{\rm d}\sigma}{{\rm d}\Omega} = r_{\rm e}^2 ({\rm Sin}[\theta])^2,$$ where $\theta$ is the angle between the XFEL polarisation and the direction of the detector, which is $\pi/2$ in the condition of the experiment, hence ${\rm d}\sigma/{\rm d}\Omega = r_{\rm e}^2$. Therefore, the intensity at the detector is $$(r_{\rm e}^2 \Omega n z) \times {\rm Incident ~photons},$$ where $n$ is the number density of electrons, and $z=12.5 \mu m$ is the thickness of the material. The number of incident photons is $\frac{W_{\rm tot}\times 1.1\times 10^{-3}}{W_{\rm photon}}$

Now we further assume that all electrons are bound, which gives $n\approx\frac{\rm 8.9 \times 10^3 kg/m^3~\times6.02\times 10^{23} /mol}{\rm 58 \times 10^{-3}~kg/mol}\approx 6\times 10^{30}{\rm /m^3}.$ The Thomson scattering from those bound electrons, without lattice enhancement, should be (note that 342 pluses are performed in this experiment):

$$342\times (2.8\times 10^{-15}{\rm m})^2\times6 \times 10 ^{-4}\times6\times 10^{30}{\rm /m^3}\times12.5 \mu {\rm m}\times\frac{1.6~{\rm mJ} \times1.1\times 10^{-3}}{9000~{\rm eV}}\approx1.5\times 10^5.$$

However, this number, being 3 orders of magnitude lower than the Kα feature, is much smaller than what is observed, which indicates that bound electrons cannot create such a strong scattering without lattice interference, even if all the electrons are bounded.

Going back to the Fe data, In this figure, the main peak remains while the Kα peak is no longer visible. This may be because of the strong background noise, or because the beam is not focused well enough. However, the above discussion still applies as the main peak feature should be some 3 orders of magnitude lower than the Kα feature if there were no lattice effect.

2.2 The cut-off feature

Although the elastic Thomson scattering without lattice effect fails to explain the main peak feature, it actually can be applied to explain this cut-off feature. If the "bound electron" in the previous discussion is changed to: "free electrons", then the conclusion is "the Thomson scattering from free electrons should be 3 orders of magnitude lower the Kα peak", which shows an agreement with the data. So if this feature is coming from inelastic Thomson scattering, then it should be from the high energy free electrons (non-thermal electrons).

Alternatively, The radiative recombination from non-thermal electrons can also create such a feature. Thus, a more detailed analysis is needed. The idea is to find how many non-thermal electrons at what energy is required to produce such a feature, i.e., to create ~ $10^5$ photons at 10 to 11 keV.

3. XRTS

The first important thing in doing an XRTS analysis is to find the scattering parameter $\alpha=\frac{1}{k\lambda_{\rm s}}$,
where $k={\frac{\Delta p}{\hbar}}$ is the change of the photon wave vector (essentially the transferred momentum $\Delta p$) in the scattering, and $\lambda_{\rm s}=\sqrt{\frac{\epsilon_0k_BT}{n{q_e}^2}}$ is the Debye length of the plasma. For a photon with an energy of 9 keV and nearly 180 degrees, backward scattered, given that the number density of the electrons is of the order $5\times 10^{30} {\rm m}^{-3}$, and the temperature of the electrons $k_BT$ is of the order $1 {\rm keV}$, the scattering parameter is of the order $1\times 10^{-1}$. Hence the scattering is non-collective, and the energy shift of photons, as well as the number of scattered photons, can be easily calculated.

3.1 Energy analysis

To produce electrons at 3 keV above the XFEL photon energy, we need a relativistic description of the scattering process:

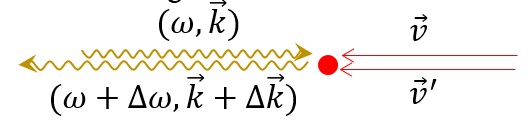
From energy and momentum conservation:

$$\hbar \omega + E_{\rm e} = \hbar \omega'+E_{\rm e}';$$

$$\frac{\hbar \omega}{c} - \frac{\sqrt{(E_{\rm e}+m_{\rm e}c^2)^2-m_{\rm e}^2c^4}}{c}=\frac{\hbar \omega'}{c} - \frac{\sqrt{(E_{\rm e}'+m_{\rm e}c^2)^2-m_{\rm e}^2c^4}}{c}.$$
Here I list some of the scattered photon energies under non-thermal electron energies.

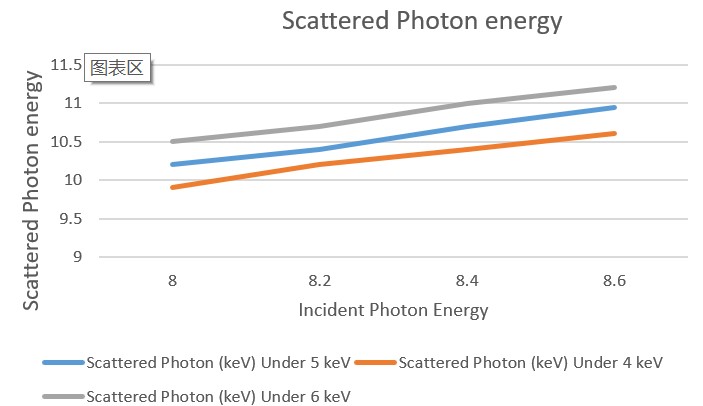
By comparing the energy shift with the data, it is clear that we are looking for non-thermal electrons at 4 to 6 keV. However, This energy interval seems to be vacant as it located between the L shell photo-ionised electrons and the Auger electrons. (It seems that it sits on the tail of Auger electrons. However, this drawing is schematic as it only shows the possibility of electrons, not a probability.)

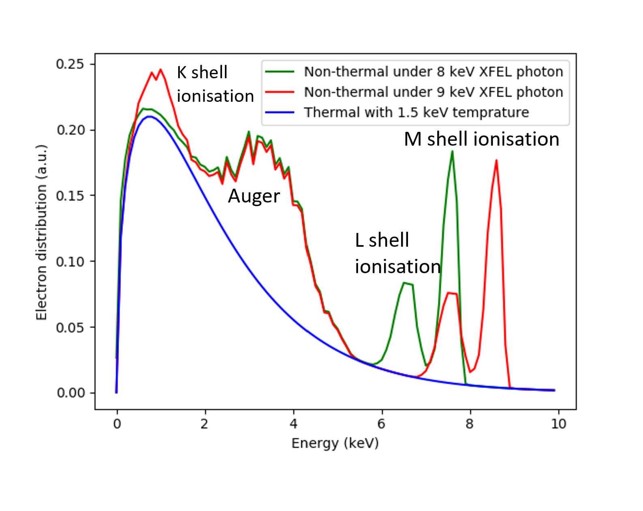
3.2 Intensity analysis

The intensity of XRTS in relatively simple as it follows the same equation (Again, 342 images in this run):

$$342 \times (r_{\rm e}^2 \Omega n z) \times {\rm Incident ~photons}=10^5.$$

Now the number of the incident photon is $10^3$ larger as the beam transmission is "full" (compared with Ni data). Thus it requires $n\approx5\times 10^{27}/{\rm m^3}$. As the number of electrons in a fully ionised plasma is about $5\times 10^{30}$, it means about 0.1% of the electrons are at 5 keV.

4. Radiative Recombination

As the K-shell Ionisation potential for highly ionised Fe is about 2 keV, this feature can also be a result of Radiative recombination.

4.1 Energy analysis

The following figure demonstrates the energy relationship:

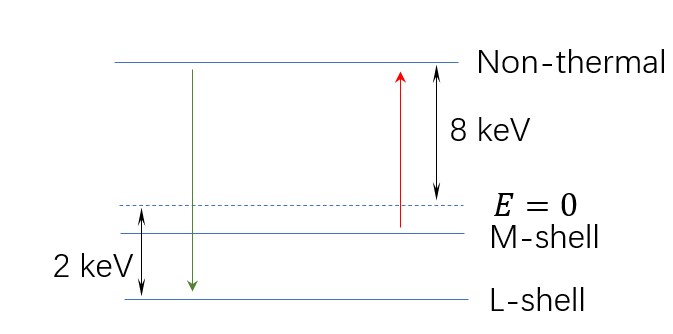
When XFEL photons with energies 8 to 9 keV hit the M-shell, they photo-ionise the M-shell electrons and creates non-thermal electrons at ~8 keV. These electrons emits photons with energies 10 keV when they recombine in L-shell. This energy relationship also explains the feature at 10 to 11 keV.

4.2 Internsity analysis

The intensity of recombination depends on both the density of the electrons ($n_{\rm e}$) and the number of ions ($N_{\rm ion}$):

$$342\times N_{\rm ion}n_{\rm e}v_{\rm e}[E]\sigma_{\rm RR}[E] \Delta t\times\Omega=10^5,$$ where $v[E]=\sqrt{\frac{2E}{m_{\rm e}}}$ and $\Delta t$ is the pulse duration. The radiative recombination cross-section $\sigma_{\rm RR}[E]$ can be found on the FLYCHK manual paper:

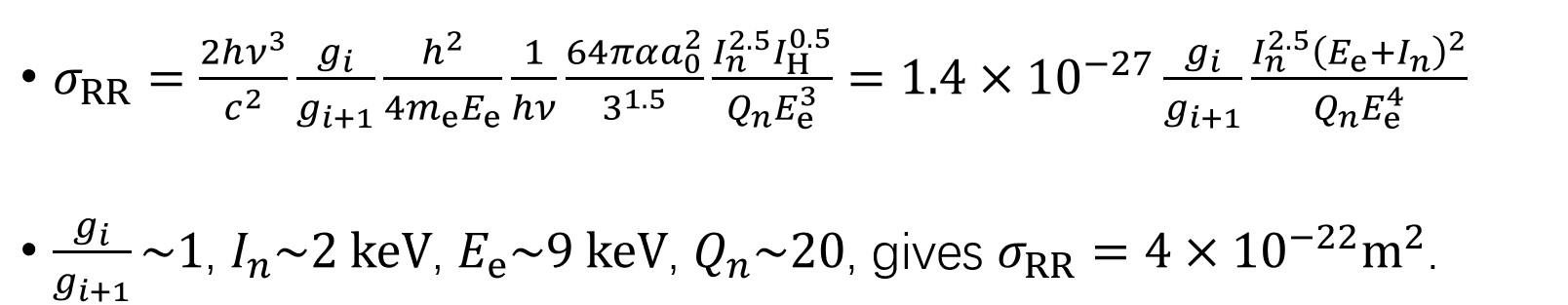
From the eLog, $\Delta t=10 ~{\rm fs}$, and $N_{\rm ion}$ can be estimated given the ion density should be some 1/20 of the electron density, hence $2\times 10^{29}$, and the size of the spot is ~ 0.1 μm,

This gives the density of the electrons: $n_{\rm e}\approx 3 \times 10^{24}/{\rm m^3}$.

5. Some Very Preliminary Conclusion

It will be helpful to list the results above:

Photon Process	XRTS	RR
Electron Energy	4 to 5 keV	~8 keV
Electron Producing Machenism	(?) Auger decay	Photo ionisation
density requirment for producing $10^5$ photons	$5\times10^{27}/{\rm m^{-3}}$	$3\times10^{24}/{\rm m^{-3}}$

And thus we can have some very preliminary conclusions:

• If the feature is coming from RR, then PI from L-shell can be responsible for producing 8 keV electrons.
• However, if this comes from XRTS, then it seems that Auger decay is less possible for producing 4 to 5 keV electrons.
• If the same number of electrons are produced by Auger decay and Photo-ionisation, then the signal from RR will be 3 orders of magnitudes stronger than XRTS.

Future Work

• The radiative recombination result can be obtained once CCFLY non-thermal module is ready.
• An XRTS module is under development and needs to be integrated into CCFLY.