Ronchi Reports

Ronchi

Report 0 (Week 0 to Week 2)

I. INTRODUCTION

The main part of the past two weeks' work is about the understanding of Ronchi, basically on physical principles and mathematical methods. We would like to make a check on these to see if the physical part is well-understood. If it is so then a proramming work will get started from next week.

II. PROGRESS

My understanding on this topic:

• The main issue is to reconstruct the wavefront of FELs using double frequency shearing interferometry.

• One Ronchi target with grating constant $D$:

  • $$F[{\rm Ron}[x,y],[x,y],[k_x,k_y]]=R_{l,m}\delta(k_x-k_l)\delta(k_y-k_m)$$
  • where $k_l=\frac{2\pi}{D}l$.
  • $k_x$ $\Rightarrow$ how the EM wave propagates in $x$ direction $\Rightarrow$$\theta_x=\frac{k_x}{k_z}$ ,etc.
  • Such a pattern is expected
    

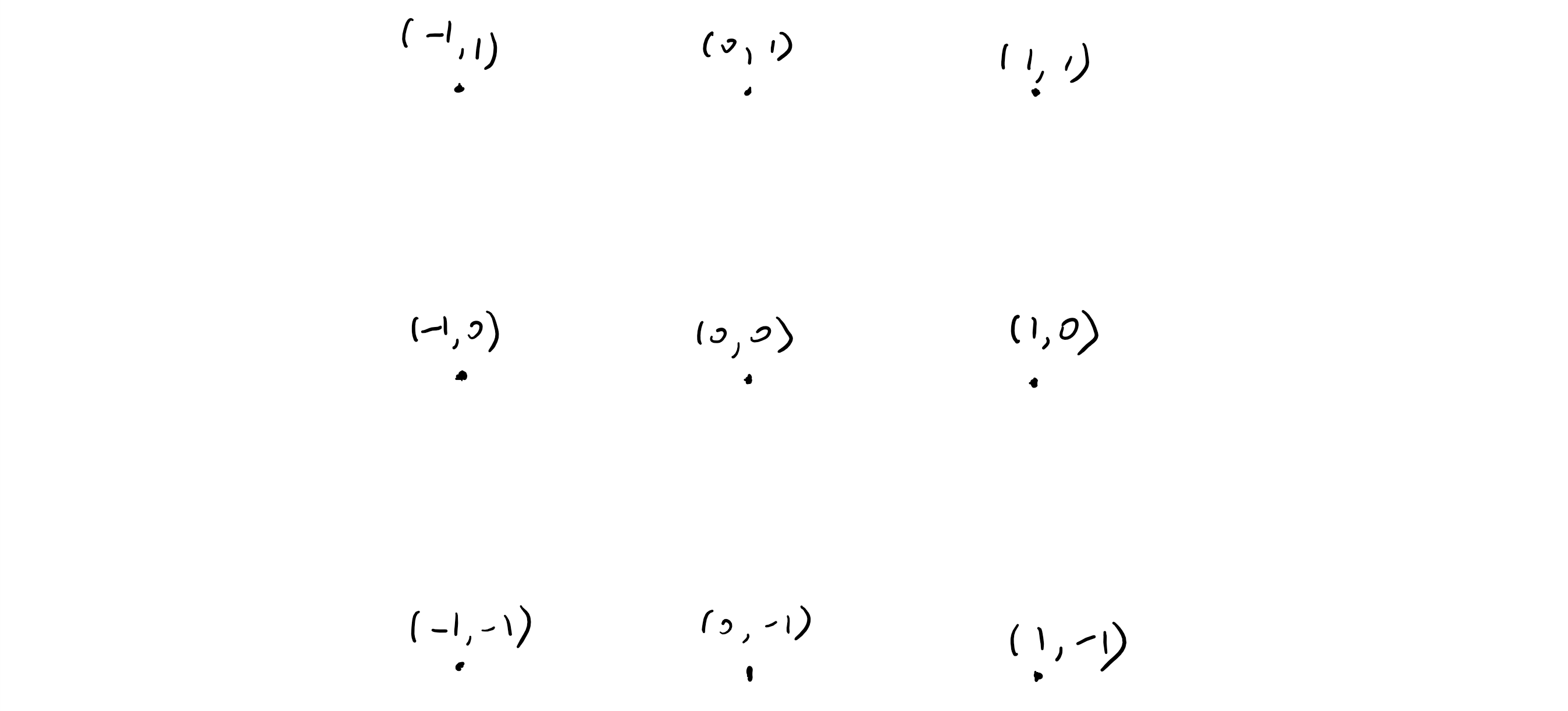
• Two Ronchi targets $D_1\dot =D_2$,placed at the nearly same position :

  • $${\rm F}[{\rm Ron}[x,y],[x,y],[k_x,k_y]]=R_{l,m}R_{p,q}\delta(k_x-k_l[D_1]-k_p[D_2])\delta(k_y-k_m[D_1]-k_q[D_2])$$
  • Since $D_1\dot =D_2$, $(l,p)=(0,1)$ and $(l,p)=(1,0)$ gives a $k_x$ close to $k_1$ in single gratting.
  • $(l,p)=(-1,2)$, etc. also gives a close $k_x$, adjust the parameter $\Rightarrow$$R$ reduces fast with large $l,m$$\Rightarrow$don't need to consider any more.
  • New pattern
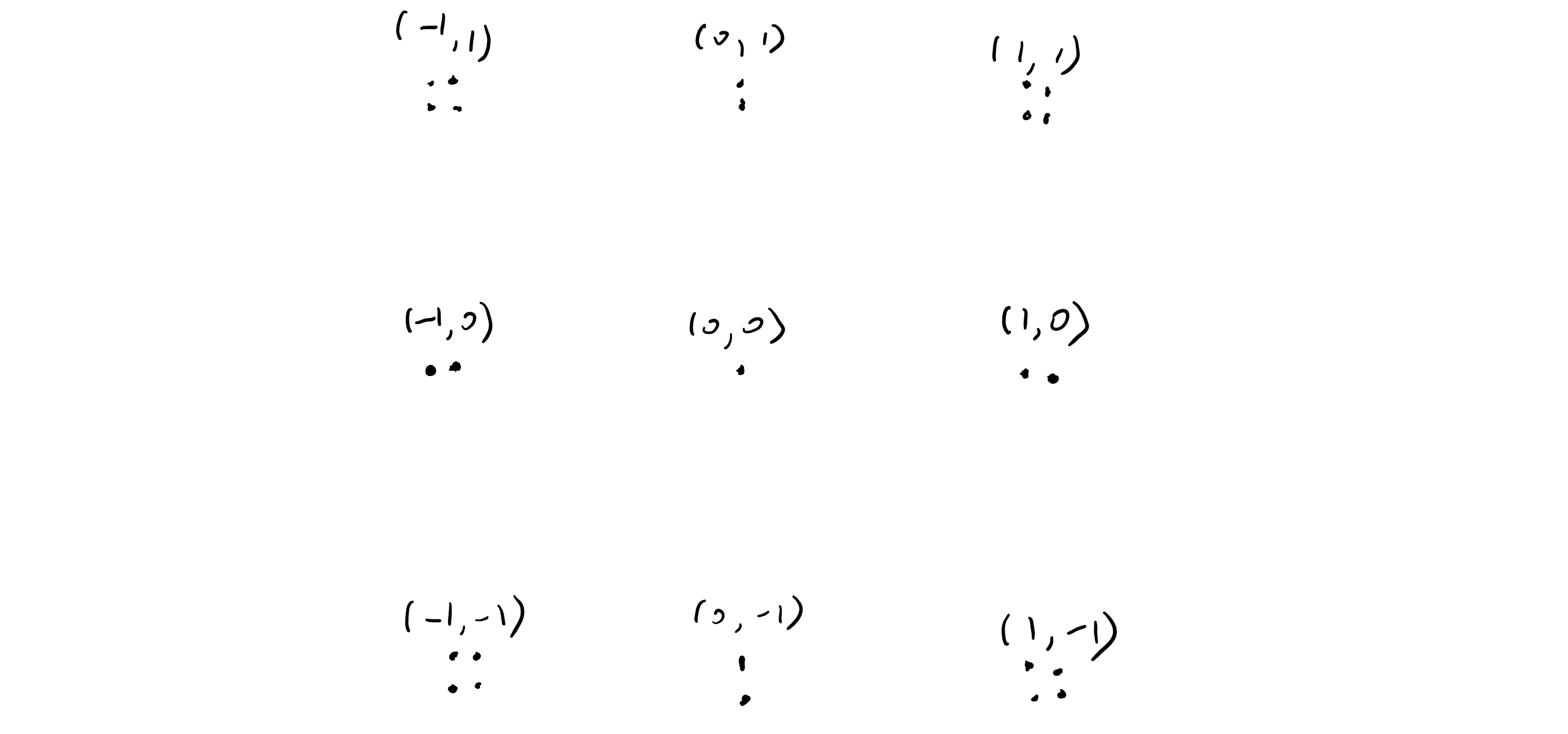
• For a beam with diameter $\Rightarrow$ Interference
  
  • Only consider (0+1,0+0) with (1+0,0+0), the other three are the same.
  • One can prove $$\vec {\tilde E}[x,y,z_c]=\frac{1}{2\pi}{\rm P}_{z_c}[x,y]\sum_{l,m,p,q}R_{l,m}R_{p,q}{\rm e}^{i\phi_{l,m,p,q}}\left(-\frac{{\rm i}k}{2\pi z_c}\right){\rm e}^{{\rm i}kz_c}\\\cdot {\rm F}[\vec {\tilde E}[x',y',0],[x',y'],[{\frac{k}{z_c}(x-x'_{l,p})},\frac{k}{z_c}(y-y'_{m,q})]]{\rm e}^{{\rm i}(k_{l,p}\frac{z_1}{z_c}x+k_{m,q}\frac{z_1}{z_c}y)}$$
  • $\phi_{l,m,p,q}=\frac{1}{2}\left(\frac{z_1}{z_c}-1\right)(k_{l,p}x_{l,p}+k_{m,q}y_{m,q})$
  • $k_{l,p}=k_l[D_1]+k_p[D_2]$, $x_{l,p}=\frac{2\pi z_1}{k}\left(\frac{l}{D_1}+\frac{p}{D_2}\right)$, $x'_{l,p}=\frac{k_{l,p}}{k}(z_c-z_1)$
  • for 0+1: $$\vec {\tilde E}[x,y,z_c]=\frac{1}{2\pi}{\rm P}_{z_c}[x,y]R_{0,0}R_{1,0}{\rm e}^{i\phi_{0,0,1,0}}\left(-\frac{{\rm i}k}{2\pi z_c}\right){\rm e}^{{\rm i}kz_c}\\\cdot {\rm F}[\vec {\tilde E}[x',y',0],[x',y'],[{\frac{k}{z_c}(x-x'_{0,1})},\frac{k}{z_c}(y-y'_{0,0})]]{\rm e}^{{\rm i}(k_{0,1}\frac{z_1}{z_c}x+k_{0,0}\frac{z_1}{z_c}y)}$$
  • for 1+0: $$\vec {\tilde E}[x,y,z_c]=\frac{1}{2\pi}{\rm P}_{z_c}[x,y]R_{1,0}R_{0,0}{\rm e}^{i\phi_{1,0,0,0}}\left(-\frac{{\rm i}k}{2\pi z_c}\right){\rm e}^{{\rm i}kz_c}\\\cdot {\rm F}[\vec {\tilde E}[x',y',0],[x',y'],[{\frac{k}{z_c}(x-x'_{1,0})},\frac{k}{z_c}(y-y'_{0,0})]]{\rm e}^{{\rm i}(k_{1,0}\frac{z_1}{z_c}x+k_{0,0}\frac{z_1}{z_c}y)}$$
  • Since$R_{1,0}=R_{0,1}$,we have the phase difference:
    $\Delta \phi[x,y]=\phi_{0,0,1,0}-\phi_{1,0,0,0}+\Delta_{[ x'_{1,0}-x'_{0,1}]}\varphi[x-x'_{1,0},y]+(k_{0,1}-k_{1,0})\frac{z_1}{z_c}x$
  • with $\Delta_{x'}f[x]=f[x+x']-f[x]$
  • shear $s:=x'_{1,0}-x'_{0,1}=\frac{k_{1,0}-k_{0,1}}{k}(z_c-z_1)=\frac{2\pi}{k}(D_1^{-1}-D_2^{-1})(z_c-z_1)\equiv$ displacement between 0+1 and 1+0
  • $(k_{0,1}-k_{1,0})\frac{z_1}{z_c}x=2\pi\frac{z_1}{z_c}(D_1^{-1}-D_2^{-1})x=k'x$
  • $\phi_{\rm c}:=\phi_{0,0,1,0}-\phi_{1,0,0,0}$ is not relevent to either $x$ or $y$.
  • $\Delta \phi[x,y]=\phi_{\rm c}+\Delta_s\varphi[x-x'_{1,0},y]+k'x$
  • Principles are the same but one can not expect the $x$ and $y$ directions are always in the gratting directions $\Rightarrow$ generalize to $\Delta \phi[\vec r]=\phi_{\rm c}+\Delta_\vec s\varphi[\vec r-\vec r'_{1,0}]+\vec k'\cdot \vec r$
• Wavefront Reconsturction
  
  • Fringes: $$I[x,y]=\left|\vec {\tilde E}_{0,0,1,0}+\vec {\tilde E}_{1,0,0,0}\cdot{\rm e}^{{\rm i}\Delta\phi[\vec r]}\right|^2\\=2I_0(1+{\rm Cos}[\Delta\phi[\vec r]])=2I_0+I_0\left({\rm e}^{{\rm i}\Delta\phi[\vec r]}+{\rm e}^{-{\rm i}\Delta\phi[\vec r]}\right)\\=2I_0+I_0\left({\rm e}^{{\rm i}(\phi_{\rm c}+\Delta_\vec s\varphi[\vec r-\vec r'_{1,0}]+\vec k'\cdot \vec r)}+{\rm e}^{-{\rm i}(\phi_{\rm c}+\Delta_\vec s\varphi[\vec r-\vec r'_{1,0}]+\vec k'\cdot \vec r)}\right)$$
  • $${\rm F}[I[x,y],[x,y],[k_x,k_y]]=8\pi^2 I_0\delta[k_x]\delta[k_y]\\+I_0{\rm F}[{\rm e}^{{\rm i}(\Delta_\vec s \varphi[\vec r-\vec r'_{1,0}]+\phi_{\rm c})},\vec r,\vec k-\vec k']+I_0{\rm F}[{\rm e}^{-{\rm i}(\Delta_\vec s \varphi[\vec r-\vec r'_{1,0}]+\phi_{\rm c})},\vec r,\vec k+\vec k']$$
  • Note: $\Delta_\vec s\varphi[\vec r-\vec r'_{1,0}]$changes much slower than $\vec k'$,the value will be not significant away from $\vec k'$ $\Rightarrow$ filter and only keep ${\rm F}[{\rm e}^{-{\rm i}(\Delta_\vec s \varphi[\vec r-\vec r'_{1,0}]+\phi_{\rm c})},\vec r,\vec k+\vec k']$
  • a leftword translation of $k'$ will give${\rm F}[{\rm e}^{-{\rm i}(\Delta_\vec s \varphi[\vec r-\vec r'_{1,0}]+\phi_{\rm c})},\vec r,\vec k]$
  • Transform back to acquire $\Delta_\vec s \varphi[\vec r-\vec r'_{1,0}]+\phi_{\rm c}$
• Cost Function
  
  • define $\varphi'[\vec r]=\varphi[\vec r-\vec r'_{1,0}]$
  • replace $\vec r$ into pixels $(i,j)$
  • acquire from the fringes for shearing vector $\vec s$:$\phi_{i,j,\vec s}=\Delta_\vec s \varphi'_{i,j}+\phi_{{\rm c},\vec s}$
  • both $\Delta_\vec s \varphi_{i,j}$ and $\phi_{{\rm c}, \vec s}$ are unknow.
  • Least Square Approximation: minimize: $$\sum_{i,j}(\phi_{i,j,\vec s}-\Delta_\vec s \varphi'_{i,j}-\phi_{{\rm c},\vec s})^2$$
  • Mask function: $1_{i,j,\vec s}=1$ where good data can be acquired $1_{i,j,\vec s}=0$ elsewise.
  • Cost function $$u^2_{\vec s}=\sum_{i,j}(\phi_{i,j,\vec s}-\Delta_\vec s \varphi'_{i,j}-\phi_{{\rm c},\vec s})^2\cdot 1_{i,j,\vec s}$$
• Smoothness:
  
  • if one solution $\varphi'_{i,j}$ has been found.
  • consider any function $\varphi''_{i,j}$ with peroid $\vec d|\vec s$
  • $\varphi''_{(i,j)+\vec d}=\varphi''_{(i,j)}\Rightarrow\varphi''_{(i,j)+\vec s}=\varphi''_{i,j}\Rightarrow\Delta_\vec s\varphi''_{i,j}=0$
  • $\varphi'_{i,j}+\varphi''_{i,j}$ is also a solution.
  • to get rid of this consider second order derivitive
  • $\varphi''_{i,j}$ has smaller period $\Rightarrow$ bigger second order derivitive
  • Regularizer: $$\zeta_x^2=\sum_{i,j}(\varphi'_{i-1,j}-2\varphi'_{i,j}+\varphi'_{i+1,j})^21_{i-1,j}1_{i+1,j}$$ $$\zeta_y^2=\sum_{i,j}(\varphi'_{i,j-1}-2\varphi'_{i,j}+\varphi'_{i,j+1})^21_{i-1,j}1_{i+1,j}$$
  • where $1_{i,j}$ is the mask function of the aperture of the beam.
  • minimize the regularizer $\Rightarrow$ minimize second order derivitive$\Rightarrow$minimize$\varphi''_{i,j}$

• Total Cost Function

  • Set $\beta$ to evaluate the weight of Regulizer
  • Consider shearing from different directions
  • $$u^2=\sum_{\vec s}u_\vec s^2+\beta (\zeta_x^2+\zeta_y^2)$$
  • minimize$\Rightarrow$partial derivitives=0
  • define $\vec p=(i,j), \vec q=(k,l)$
  • $$\frac{\partial u^2}{\partial \varphi'_{\vec q}}=\sum_{\vec s}\frac{\partial u^2_\vec s}{\partial \varphi'_{\vec q}}+\beta \left(\frac{\partial \zeta_x^2}{\partial \varphi'_{\vec q}}+\frac{\partial \zeta_y^2}{\partial \varphi'_{\vec q}}\right)$$
  • $$\frac{\partial u^2_\vec s}{\partial \varphi'_{\vec q}}=21_{\vec q,\vec s}(\phi_{\vec q,\vec s}-\Delta _\vec s \varphi'_{\vec q}-\phi_{{\rm c},\vec s})-21_{\vec q-\vec s,\vec s}(\phi_{\vec q-\vec s,\vec s}-\Delta _\vec s \varphi'_{\vec q-\vec s}-\phi_{{\rm c},\vec s})\\=-2\Delta_{-\vec {s}}(1_{\vec q,\vec s}(\phi_{\vec q,\vec s}-\Delta _\vec s \varphi'_{\vec q}-\phi_{{\rm c},\vec s}))$$
  • $$\frac{\partial \zeta_x^2}{\partial \varphi'_{\vec q}}=2(\varphi'_{\vec q}-2\varphi'_{\vec q+(1,0)}+\varphi'_{\vec q+(2,0)})1_{\vec q}1_{\vec q+(2,0)}\\-4(\varphi'_{\vec q+(-1,0)}-2\varphi'_{\vec q}+\varphi'_{\vec q+(1,0)})1_{\vec q+(-1,0)}1_{\vec q+(1,0)}+2(\varphi'_{\vec q+(-2,0)}-2\varphi'_{\vec q+(-1,0)}+\varphi'_{\vec q})1_{\vec q+(-2,0)}1_{\vec q}$$
  • $$\frac{\partial \zeta_y^2}{\partial \varphi'_{k,l}}=2(\varphi'_{\vec q}-2\varphi'_{\vec q+(0,1)}+\varphi'_{\vec q+(0,2)})1_{\vec q}1_{\vec q+(0,2)}\\-4(\varphi'_{\vec q+(0,-1)}-2\varphi'_{\vec q}+\varphi'_{\vec q+(0,1)})1_{\vec q+(0,-1)}1_{\vec q+(0,1)}+2(\varphi'_{\vec q+(0,-2)}-2\varphi'_{\vec q+(0,-1)}+\varphi'_{\vec q})1_{\vec q+(0,-2)}1_{\vec q}$$
  • $$\frac{\partial u^2}{\partial \phi_{{\rm c}, \vec s}}=\frac{\partial u_\vec s^2}{\partial \phi_{{\rm c}, \vec s}}=-2\sum_{\vec p}1_{\vec p,\vec s}(\phi_{\vec p,\vec s}-\Delta_\vec s\varphi'_{\vec p}-\phi_{{\rm c},\vec s})$$

• Non-integer Shearing

  • Sometimes one should consider non-integer value shearing $\Rightarrow$ Interpolation
  • $$\hat D_\vec s\varphi'_\vec p=\varphi'_{\vec p-\vec s}\dot = \sum_\vec r A_{\vec p,\vec r,\vec s} \varphi'_\vec r$$
  • Bilinear interpolation $\Rightarrow$ For given $\vec p$, only 4 $\vec q$ gives non-zero $A_{\vec p,\vec r,\vec s}$
    
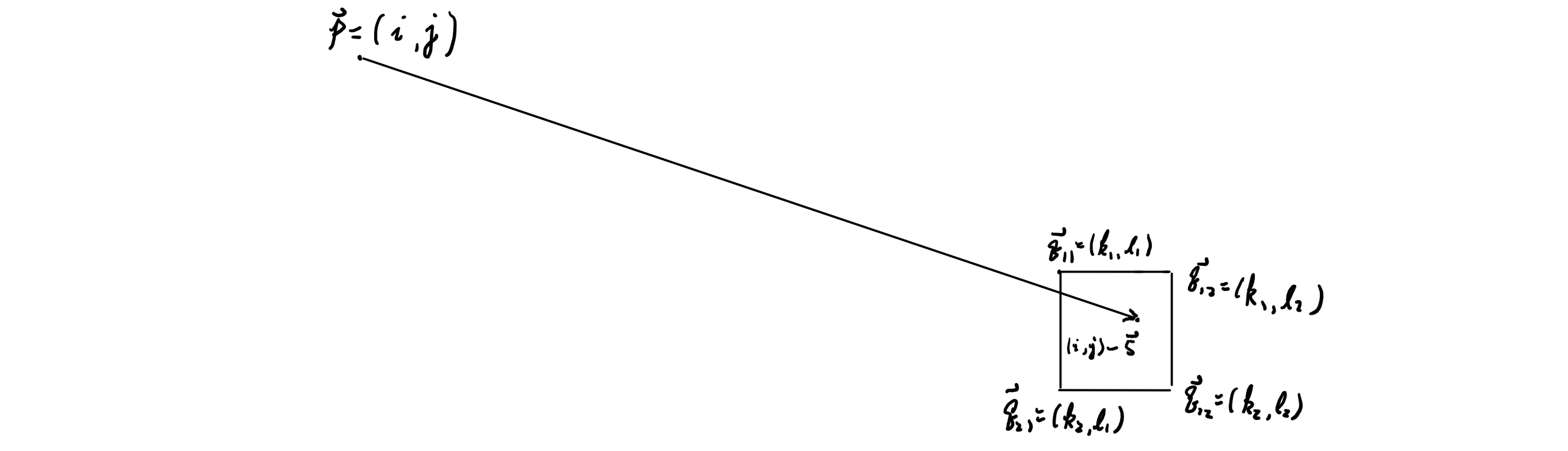
  • Set $\vec p-\vec s=(x,y)$, we find the four adjacent grid points$\vec r_{1,1}=(k_1,l_1)$, $\vec r_{1,2}=(k_1,l_2)$, $\vec r_{2,1}=(k_2,l_1)$, $\vec r_{2,2}=(k_2,l_2)$
  • $$A_{\vec p,\vec r_{1,1}}=(k_2-x)(l_2-y) \\A_{\vec p,\vec r_{1,2}}=(k_2-x)(y-l_1) \\A_{\vec p,\vec r_{2,1}}=(x-k_1)(l_2-y) \\A_{\vec p,\vec r_{1,1}}=(x-k_1)(y-l_1)$$

III. SUMMARY

The main steps of this project should be

• fourier transform the intensity information acquired
• filter the lower frequencies to get a single peak
• translate the peak so that the center should be at zero
• transform back to get phase information
• Find the shear vector and the mask functions
• Optimizing Cost function

IV. FUTURE WORK

By next week these works will be carried out

• Finish the SLAC trainning so that I will have the acces to the logbook
• write a demo of the programme, see if it works.

Report 1 (Week 3 to Week 4)

I. Introduction

The main isssue if this stage of work is to acquire the phase information at the target plane from the image. We mainly used the method discribed in the report last week. The idea comes from Takeda et al.(1982)

II. PROGRESS

• The first step is to acquire the mask function. At this stage the mask function is not good enough to detect all the interference areas. Hence some adjust have to be used. In the next version a more rubust mask function should be acquired.
• The following part is based on one interfering area of p255, which is shown:
• to acquire the phase information we fft the image

f=np.fft.fft2(Raw) #Raw is the image with mask
Transformed=np.fft.fftshift(f)
Abs=abs(Transformed)

this is what we get from fft:
the two light spot indicates the main space frequiencies caused the interference, if we put the center of one of two peaks at $0$ then the interference will be filtered out and the rest information is all about the phase we want.

• We only want to keep one light spot of the fft diagram. Therefore it is useful to tilter DC part.

for i in range(0,2047):
    for j in range(0,2047):
        if (i-1023)**2*(j-1023)**2<4000000\\emperical parameter,may not be universal:
            Abs[i][j]=0

• the result is shown:

• Finding the maximun of the left half of the image will give the center if the peak

a=np.empty(shape=[2048, 2048])
for i in range(0,1023):
    for j in range(0,2047):
        a[i][j]=Abs[i][j]
m, n = a.shape
index = int(a.argmax())
x = int(index / n)
y = index % n

• We only want the information near the peak:

for i in range(0,2047):
    for j in range(0,2047):
        if (i-x)**2+(j-y)**2>10000:
            Abs[i][j]=0
            Transformed[i][j]=0

• putting it at the center:

b=f   #set up a complex matrix with f
for i in range(0,2047):
    for j in range(0,2047):
        b[i][j]=0   #set b as 0
for i in range(-100,100):
    for j in range(-100,100):
        b[1023+i][1023+j]=Transformed[x+i][y+j]   

• And we transform back to acquire the phase information

ff=np.fft.ifftshift(b)
Result=np.fft.ifft2(ff)
Phase=np.zeros((2048, 2048))
for i in range(0,2047):
    for j in range (0,2047):
        Phase[i][j]=cmath.phase(cmath.log(Result[i][j]))*Mask[i][j]

• This is the final information we acquire
  

• To take a closee look:

• The maxinum difference between pixels is no more than 1 rad so the jump in the picture should not be caused by anything ralated to a $2\pi$ difference. Though such a $2\pi$ connection function is also included:

for i in range(0,2047):
    for j in range(0,2046):
        if Phase[i][j]-Phase[i][j+1]>0.9*2*math.pi:
            print(i,j)
            for k in range(j+1,2047):
                Phase[i][k]+=2*math.pi
        elif Phase[i][j]-Phase[i][j+1]<-0.9*2*math.pi:
            print(i,j)
            for k in range(j+1,2047):
                Phase[i][k]-=2*math.pi

III. SUMMARY

• The way of finding a musk function is still in progress. Though one method has already been found, it dose not always works for all the pictures.
• The result of fft revealed the phase information, which has been therotically discussed in Report0.

IV. FUTURE WORK

The future work is listed in the order of priority:

• Strating to optimize the cost function
• To ristrict the fft process within the mask area so that the programme will run faster.
• To see how window function will affect the fft process and the result
• To find out a more rubust way to find mask function.

Report 2 (Week 5)

I. INTRODUCTION

The issue of this week is to improve the retrieved phase. The main difference of this week from last week is that a hanning window is applied. Also, The picture is not cut before fft.

II. PROGRESS

• p255 is still used in this work. The main part of the programme is similar to the previous version,expect that the mask function is applied after phase retrieve.
• The window function is

window=scipy.signal.hanning(51, sym=True) 
for i in range(0,2048):
    for j in range(0,2048):
        if abs(i-x)>25 or abs(j-y)>25:
            Abs[i][j]=0
            Transformed[i][j]=0
        else:
            Abs[i][j]*=window[i-(x-25)]*window[j-(y-25)]
            Transformed[i][j]*=window[i-(x-25)]*window[j-(y-25)]

• the result is shown(after centered):
  

• One may find smaller structures within the peak. These structures had already appeared once the fft is done, which is different from the previous work. Here a diagram of fft is shown after DC filtering but before windowing.

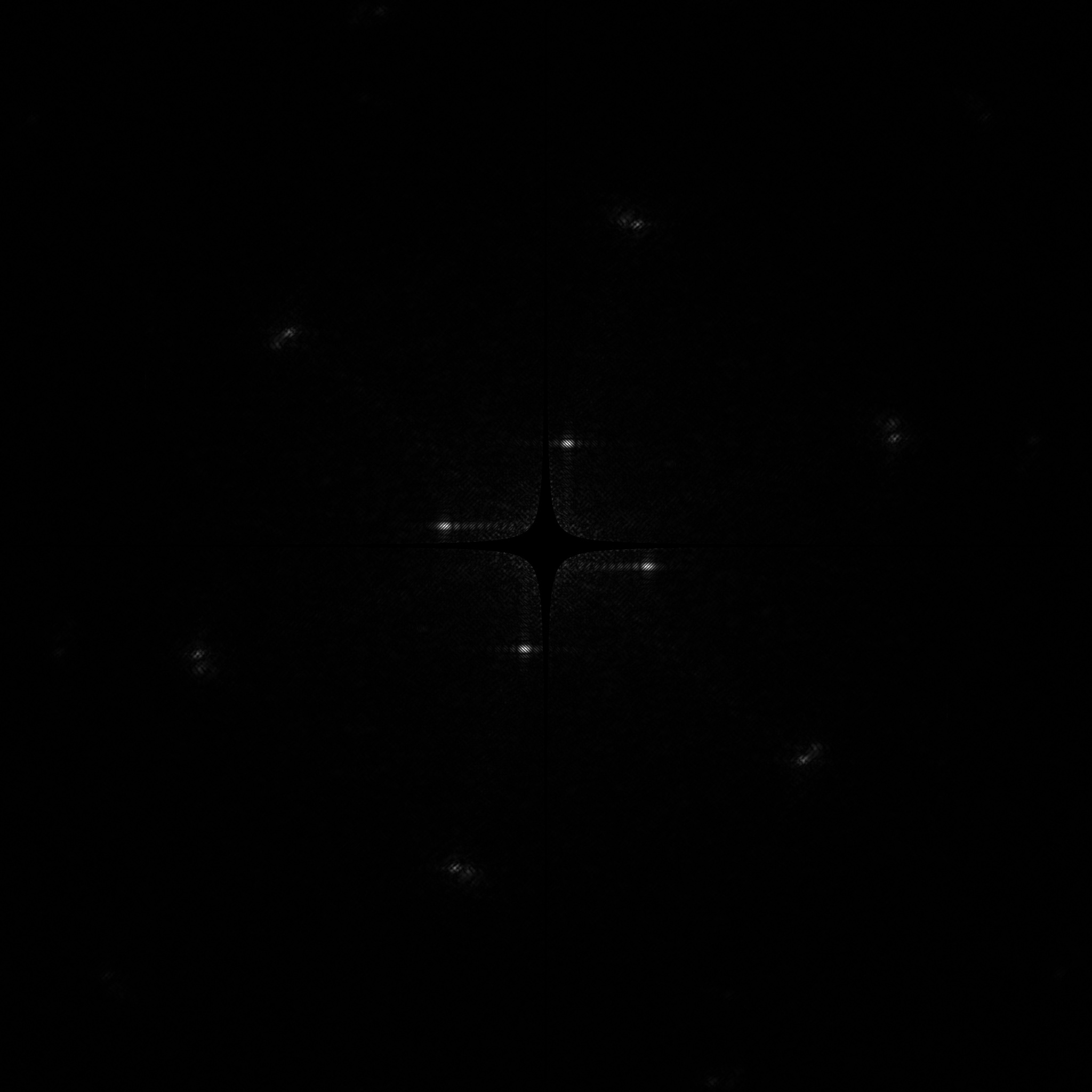
• For sanity check, a diagram witout centering is also used to generate phase information and after overlaying with the raw image:
  
  One can see that they maches extreamly well.
• The retrieved phase (the outer grey part is caused by the mask):
  
  with maximun value 0.514(darkest) and minimun value -1.01(lightest) in rads.
• Also some other variations on window was made to see how the phase changes. This is a 30*30 window with max=0.508 and min=-0.773.:
  
  And a 40*40 one with max=0.499 and min=-0.909.:
  
  And also a 60*60 one with max=0.511 and min=-1.077.:
  

III. SUMMARY

• The phase retrived phase showed big difference with the precious results.
• The sanity check showed that the retrived phae might be correct.
• We can see that the result becomes stable when the window is bigger than 50*50. It is proper to use a 50*50 window.

IV. FUTURE WORK

The future works are the same with those in Report1. The cost functon is of the most importance.

Report 3 (Week 6 and 7)

I. SUMMARY
The main part of the work in the past two week focus on the Cost Function and the derivities. Also the codes are reorganized so that the optimazation can run faster. Still, p255 is used.

II. PROGRESS

The programme is sperated into two parts, the first in the Link Function, which is used to retrieve the phase and link them. In this version all the fransformations are done within a 251($y$ direction)$\times$151($x$ direction) square.

• The Link(start,end) function is to retrieve and link phase for all the pictures with p number from start to end, for example, Link(255,256) gives the linked retrieved phase of 255. This is realized by:

def Link(start,end):
    for i in range(start,end): # i is p number
        for j in range(1,5): # j is the area
            link(15,30,i,j) # 15: the length of the mask, 30: the intensity of the DC Filter

where area range from 1 to 5 indecates the part of the picture.( area==1 indecates upper-left rectangle, etc )

• The link(length,Intensity,pnumber,area) function is to retrieve and link the phase of one of the 4 rectangle areas in a picture with a certain p number. This is realized by:

def link(length,Intensity,pnumber,area):
    Phase=getphase(length,Intensity,pnumber,area)
    for i in range(0,251):
        for j in range(0,150):
            if Phase[i][j]-Phase[i][j+1]>0.95*2*math.pi:
                for k in range(j+1,151):
                    Phase[i][k]+=2*math.pi
            elif Phase[i][j]-Phase[i][j+1]<-0.95*2*math.pi:
                for k in range(j+1,151):
                    Phase[i][k]-=2*math.pi
    for j in range(0,151):
        for i in range(0,250):
            if Phase[i][j]-Phase[i+1][j]>0.95*2*math.pi:
                for k in range(i+1,251):
                    Phase[k][j]+=2*math.pi
            if Phase[i][j]-Phase[i+1][j]<-0.95*2*math.pi:
                for k in range(i+1,251):
                    Phase[k][j]-=2*math.pi
    plt.imshow(Phase)
    plt.colorbar()
    plt.axis()
    plt.show()
    np.savetxt('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\LinkedRetrivedPhase%d-%d.txt'%(pnumber,area,pnumber,area),Phase)
    return Phase

The code is long but the very main part is line 2 and line3-18.line 3-18 is to link phase. Line 2 is the function that can retrieve phase. The result is saved by a txt document so that during the optimization the programme can read very easily (line 23).

• The getphase(length,Intensity,pnumber,area) function is realized by

def getphase(length,Intensity,pnumber,area):
    ff=np.fft.ifftshift(Move(length,Intensity,pnumber,area))
    Result=np.fft.ifft2(ff)
    Phase=np.zeros((251, 151))
    Phase=math.phase(Result)
    plt.imshow(Phase)
    plt.colorbar()
    plt.axis()
    plt.show()
    return Phase

again only line 2 is import with the Move(length,Intensity,pnumber,area) gives centered fft result. Result gives the ifft result and phase gets the phase

• In the Move(length,Intensity,pnumber,area) function two main functions are called, one is HanningWindow(length,Intensity,pnumber,area) which gives the windowed fft result and the other is Center(Intensity,pnumber,area) which gives the peak coordinate of fft diagram.

def Move(length,Intensity,pnumber,area):
    HanningWindowed=HanningWindow(length,Intensity,pnumber,area)
    global f # from fft, f is used to create a complex matrix.
    b=f
    x=Center(Intensity,pnumber,area)[1] # peak coordinate
    y=Center(Intensity,pnumber,area)[0] # peak coordinate
    for i in range(-125,125):
        for j in range(-75,75):
            if -(length-1)/2<i<(length-1)/2 and -(length-1)/2<j<(length-1)/2:
                b[125+i][75+j]=HanningWindowed[int(y+i)][int(x+j)]
            else:
                b[125+i][75+j]=0
    Renormalizedc=c*255/np.max(c)
    cv2.imwrite('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\CenteredFFT.jpg'%(pnumber,area),Renormalizedc)
    return b

• The HanningWindow(length,Intensity,pnumber,area) function uses the result of DCFilter(Intensity,pnumber,area) which gives the result of DC Filtered fft. Also the Center(Intensity,pnumber,area) function is called.

def HanningWindow(length,Intensity,pnumber,area):
    windowed=DCFilter(Intensity,pnumber,area)
    x=Center(Intensity,pnumber,area)[1]
    y=Center(Intensity,pnumber,area)[0]
    window=scipy.signal.hanning(length, sym=True) 
    for i in range(0,251):
        for j in range(0, 151):
            if abs(i-y)<(length-1)/2 and abs(j-x)<(length-1)/2:
                windowed[i][j]*=window[int(i-y+(length-1)/2)]*window[int(j-x+(length-1)/2)]
            else:
                windowed[i][j]=0
    windowedabs=np.abs(windowed)
    RenomalizedAbs = windowedabs*255/np.max(windowedabs)
    cv2.imwrite('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\HanningWindowedFFT.jpg'%(pnumber,area),RenomalizedAbs)
    return windowed

• The DCFilter(Intensity,pnumber,area) function is realized by:

def DCFilter(Intensity,pnumber,area):
    Filtered=FFT(pnumber,area)
    for i in range(0,251):
        for j in range(0,151):
            if (i-125)**2*(j-75)**2<Intensity**2:
                Filtered[i][j]=0
    return Filtered

with the FFT(pnumber,area):

def FFT(pnumber,area):
    global f  # f is used in later functions
    f=np.fft.fft2(Raw(pnumber,area)) # a 251*151 matrix recording the intenxity information
    Transformed=np.fft.fftshift(f)
    abs=np.abs(Transformed)
    renormalizedabs=abs*255/np.max(abs)
    cv2.imwrite('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\FFTResult.jpg'%(pnumber,area),renormalizedabs)
    return Transformed

where Raw(pnumber,area)

def Raw(pnumber,area):
    result=np.zeros((251,151))
    raw = np.loadtxt('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\p%d-%d.txt'%(pnumber,area,pnumber,area))
    b,a=raw.shape
    x=int(a/2) # center
    y=int(b/2) # center
    for i in range (-125,125):
        for j in range (-75,75):
            if 0<i+y<b and 0<j+x<a:
                result[i+125][j+75]=raw[i+y][j+x]
    return result

• TheCenter(Intensity,pnumber,area)function looks long but the structure is qiute simple: since area indecates the posotion of the rectangles (1 for upper-left, etc.), we only remain that part and find the peak there.

def Center(Intensity,pnumber,area):
    a=np.zeros(shape=[251,151]) # an empty background
    FilterAbs=DCFilterAbs(Intensity,pnumber,area) # put one of the for 1/4 area on the background
    if area == 1:
        for i in range(0,125):
            for j in range(0,75):
                a[i][j]=FilterAbs[i][j]
    elif area == 2:
        for i in range(0,125):
            for j in range(75,151):
                a[i][j]=FilterAbs[i][j]
    elif area == 3:
        for i in range(126,251):
            for j in range(0,75):
                a[i][j]=FilterAbs[i][j]
    elif area == 4:
        for i in range(126,251):
            for j in range(76,151):
                a[i][j]=FilterAbs[i][j]
    m, n = a.shape # n=number of length in x, etc.
    index = int(a.argmax()) # the index of the peak
    Result=np.zeros((2))
    y = int(index / n) # find out in which row
    x = index % n # find out in which columm
    Result[0]=y
    Result[1]=x
    return Result

Line 2 creates an empty background and line 3-19 put one of the for 1/4 on the background, line 20-24 searches for the peak. Line 3 called a function DCFilterAbs(Intensity,pnumber,area) which gives the scale of the fft result after DC Filter.

• The DCFilterAbs(Intensity,pnumber,area) is realized by

def DCFilterAbs(Intensity,pnumber,area):
    DCFiltered=DCFilter(Intensity,pnumber,area)
    abs=np.abs(DCFiltered)
    renomalizedabs=abs*255/np.max(abs)
    cv2.imwrite('C:\\Users\\18217\\OneDrive\\files\\Research\\Ronchi\\data\\x287_ronchi\\%d\\%d\\filtered.jpg'%(pnumber,area),renomalizedabs)
    return abs

The retrieved phase is somehow different from these from the previous versions for area 1 to 4:




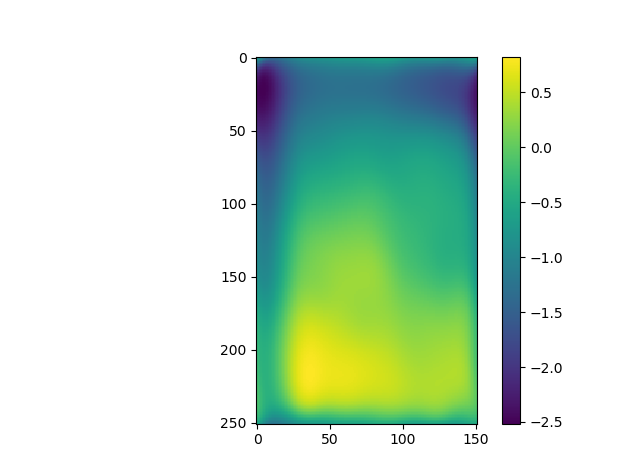
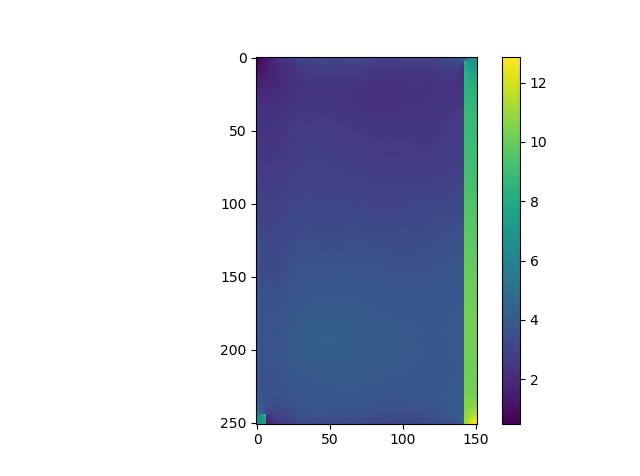
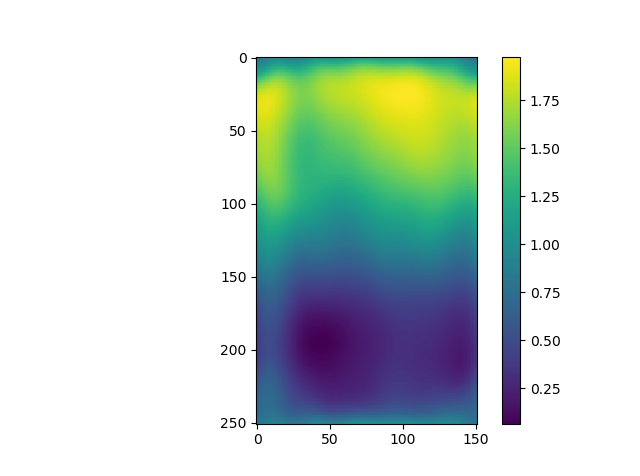
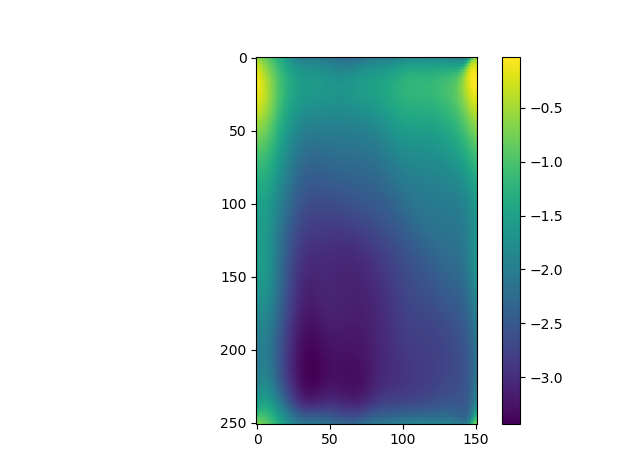
And it is quite notable that the phase for area 2 is not correctly linked although it passed the overlay phase check.

The second part is the optimazation part, with the optimazation function:scipy.optimize.fmin_l_bfgs_b(TotalCost,x,fprime=derivitive)

• The TotalCost

def TotalCost(x):
    # x is the vector containing phi and phic
    global start # starting pnumber, 255 here
    global end # ending pnumber, 256 here
    global beta # weight of regulizer
    phi=np.zeros((251,151)) # buffer to save reconstruced phase (main variable)
    phic=np.zeros((300,5)) # buffer to save reconstruced phic_s (main variable)
    for i in range(0,251):
        for j in range(0,151):
            phi[i][j]=x[151*i+j] # arrange the phis with x
    for i in range(start,end):
        for j in range(1,5):
            phic[i][j]=x[151*251+4*(i-start)+j-1] # arrange the phics with x
    sum=0
    for pnumber in range(start,end):
        for area in range(1,5):
            sum+=CostFunction(pnumber,area,phi,phic)
    sum+=beta*(Regx(phi)+Regy(phi))
    return sum

with CostFunction(pnumber,area,phi,phic):

def CostFunction(pnumber,area,phi,phic):
    global Phase
    ShearVectorX=ShearVectorx(pnumber,area)
    ShearVectorY=ShearVectory(pnumber,area)
    sum=0
    for i in range(0,251):
        for j in range (0,151):
            if i+ShearVectorY<251 and j+ShearVectorX<151:
                sum+=(Phase[pnumber][area][i][j]-Delta(i,j,ShearVectorY,ShearVectorX,phi)-phic[pnumber][area])**2
    return sum

where the Delta(y,x,Deltay,Deltax,func) function:

def Delta(y,x,Deltay,Deltax,func):
    result = func[int(y+Deltay)][int(x+Deltax)]-func[int(y)][int(x)]
    return result

and:

def Regy(phi):
    sum=0
    phiplusone=phi[1:251,:]
    phiplusone=np.insert(phiplusone,250,np.zeros(151),axis=0)
    phimunusone=phi[0:250,:]
    phimunusone=np.insert(phimunusone,0,np.zeros(151),axis=0)
    result=phimunusone-2*phi+phiplusone
    sum=np.sum(result)
    return sum

and Regx(phi) is similar

• the derivitive(x):

def derivitive(x):
    global start
    global end
    global beta
    global Phase
    phi=np.zeros((251,151))
    phic=np.zeros((300,5))
    for i in range(0,251):
        for j in range(0,151):
            phi[i][j]=x[151*i+j] # assign to phi from x
    for i in range(start,end):
        for j in range(1,5):
            phic[i][j]=x[151*251+4*(i-start)+j-1] # assign to phi from x
    result=np.zeros((251*151+4*(end-start))) # the return of the function
    matrix=np.zeros((251,151)) # to contain the derivities of phi_{i,j}
    argument=np.zeros((251,151)) # argument=Phase-Delta-phi_c, derivitive = -2Delta(argument)
    anothermatrix=np.zeros((300,5)) # to contain the derivities of phic_s
    for pnumber in range(start , end):
        for area in range(1,5):
            ShearVectorX=ShearVectorx(pnumber,area)
            ShearVectorY=ShearVectory(pnumber,area)
            for i in range(0,251):
                for j in range(0,151):
                    if i-ShearVectorY>0 and i+ShearVectorY<251 and j - ShearVectorX>0 and j+ShearVectorX<151:
                        argument[i][j]=Phase[pnumber][area][i][j]-Delta(i,j,ShearVectorX,ShearVectorY,phi)-phic[pnumber][area]
            for i in range(0,251):
                for j in range(0,151):
                    if i-ShearVectorY>0 and i+ShearVectorY<251 and j - ShearVectorX>0 and j+ShearVectorX<151:
                        matrix[i][j]+=-2*Delta(i,j,-ShearVectorX,-ShearVectorY,argument)
                    anothermatrix[pnumber][area]+=-2*(argument[i][j])
    phiplusone=phi[:,1:151]
    phiplusone=np.insert(phiplusone,150,np.zeros(251),axis=1)
    phiplustwo=phiplusone[:,1:151]
    phiplustwo=np.insert(phiplustwo,150,np.zeros(251),axis=1)
    phimunusone=phi[:,0:150]
    phimunusone=np.insert(phimunusone,0,np.zeros(251),axis=1)
    phimunustwo=phimunusone[:,0:150]
    phimunustwo=np.insert(phimunustwo,0,np.zeros(251),axis=1)
    matrix+=2*(phi-2*phiplusone+phiplustwo)-4*(phimunusone-2*phi+phiplusone)+2*(phimunustwo-2*phimunusone+phi)
    #This is to calculate the direvities of the regulizer
    phiplusone=phi[1:251,:]
    phiplusone=np.insert(phiplusone,250,np.zeros(151),axis=0)
    phiplustwo=phiplusone[1:251,:]
    phiplustwo=np.insert(phiplustwo,250,np.zeros(151),axis=0)
    phimunusone=phi[0:250,:]
    phimunusone=np.insert(phimunusone,0,np.zeros(151),axis=0)
    phimunustwo=phimunusone[0:250,:]
    phimunustwo=np.insert(phimunustwo,0,np.zeros(151),axis=0)
    #This is to calculate the direvities of the regulizer
    matrix+=2*(phi-2*phiplusone+phiplustwo)-4*(phimunusone-2*phi+phiplusone)+2*(phimunustwo-2*phimunusone+phi)
    for i in range(0,251):
        for j in range(0,151):
            if j<2 or j >148:
                matrix[i][j]=0
            if i<2 or i>248:
                matrix[i][j]=0
    for i in range(0,251):
        for j in range(0,151):
            result[151*i+j]=matrix[i][j]
    for i in range(start,end):
        for j in range(1,5):
            result[151*251+4*(i-start)+j-1]=anothermatrix[i][j]
    return result

III. SUMMARY
This part of the work is to reorganize wo that it can run faster, but it's hard to judge whether the phase information is accurate. Also the cost function and the derivities are acquired.

IV. FUTURE WORK
In week 8 a first result of the whole programme can be acuired.