Minimizing the Regularizer

Ronchi

---

BACKGROUND

• $\varphi'[x,y]$ is a 2-D function,
• The Regularizer, defined as the integration of the squared second order derivatives, discribes the fluctuation of a function $\varphi'[x,y]$, i.e.

$$\zeta_x=\iint\left(\frac{\partial^2 \varphi'}{\partial x^2}\right)^2{\rm d}x{\rm d}y$$

$$\zeta_y=\iint\left(\frac{\partial^2 \varphi'}{\partial y^2}\right)^2{\rm d}x{\rm d}y$$

• The problem is to minmize the regularizers $\zeta_x+\zeta_y$, i.e. to fnd a $\varphi'[x,y]$ that $\zeta_x+\zeta_y$ reach the minimum. One might notice that $\zeta_x\geqslant0$,$\zeta_x\geqslant0$. Analytically, we could try to find
  $$\zeta_x+\zeta_y=0$$

$$\frac{\partial^2 \varphi'}{\partial x^2}=\frac{\partial^2 \varphi'}{\partial y^2}=0$$

$$\varphi'[x,y]=Ax+By+C$$

• We are trying to use a numerical method to find this, which requires aproximate value of $\varphi'[x,y]$ at every point

• Using discrete approximation, Regularizers can be replaced with

$$\zeta_x^2=\sum_{i,j}(\varphi'_{\bar i-1,\bar j}-2\varphi'_{\bar i,\bar j}+\varphi'_{\bar i+1,\bar j})^2$$

$$\zeta_y^2=\sum_{\bar i,\bar j}(\varphi'_{\bar i,\bar j-1}-2\varphi'_{\bar i,\bar j}+\varphi'_{\bar i,\bar j+1})^2$$

• we try to find all the $\varphi'_{\bar i,\bar j}$ that could minimize the function (so here the variables are the $\varphi'_{\bar i,\bar j}$s, not $x$ and $y$)，hence we calculate the partial derivatives, let $[\bar i,\bar j]=\bar {\vec q}$, therefore
  $$\frac{\partial \zeta_x^2}{\partial \varphi'_\bar {\vec q}}=2(\varphi'_\bar {\vec q}-2\varphi'_{\bar {\vec q}+(1,0)}+\varphi'_{\bar {\vec q}+(2,0)})\\-4(\varphi'_{\bar {\vec q}+(-1,0)}-2\varphi'_{\bar {\vec q}}+\varphi'_{{\vec q}+(1,0)})+2(\varphi'_{\bar {\vec q}+(-2,0)}-2\varphi'_{\bar {\vec q}+(-1,0)}+\varphi'_\bar {\vec q})$$

$$\frac{\partial \zeta_y^2}{\partial \varphi'_\bar{\vec q}}=2(\varphi'_{\bar {\vec q}}-2\varphi'_{\bar {\vec q}+(0,1)}+\varphi'_{\bar {\vec q}+(0,2)})\\-4(\varphi'_{\bar {\vec q}+(0,-1)}-2\varphi'_{\bar {\vec q}}+\varphi'_{\bar {\vec q}+(0,1)})+2(\varphi'_{\bar {\vec q}+(0,-2)}-2\varphi'_{\bar {\vec q}+(0,-1)}+\varphi'_{\bar {\vec q}})$$

CODES

• phi is the $\varphi'$ above, the area is a 231*141 rectangle, therefore phi is a 231*141 matrix
• Regularizers

#Regx
def Regy(phi):
    sum=0
    phiplusone=phi[1:231,:]
    phiplusone=np.insert(phiplusone,230,np.zeros(141),axis=0)
    phimunusone=phi[0:230,:]
    phimunusone=np.insert(phimunusone,0,np.zeros(141),axis=0)
    result=(phimunusone-2*phi+phiplusone)**2
    sum=np.sum(result)
    return sum
#Regy
def Regx(phi):
    sum=0
    phiplusone=phi[:,1:141]
    phiplusone=np.insert(phiplusone,140,np.zeros(231),axis=1)
    phimunusone=phi[:,0:140]
    phimunusone=np.insert(phimunusone,0,np.zeros(231),axis=1)
    result=(phimunusone-2*phi+phiplusone)**2
    sum=np.sum(result)
    return sum

• TotalCost Funtion: We use vector x as the main variable of thefunction, therefore

#Total Cost
def TotalCost(x):
    phi=np.zeros((231,141))
    for i in range(0,231):
        for j in range(0,141):
            phi[i][j]=x[141*i+j] # put the x value into phi
    sum=0
    sum+=(Regx(phi)+Regy(phi))
    return sum

• The derivatives:

def derivative(x)
    phi=np.zeros((231,141))
    for i in range(0,231):
        for j in range(0,141):
            phi[i][j]=x[141*i+j]
    matrix=np.zeros((231,141)) # matrix containing derivatives to phi
    result=np.zeros((231*141)) # final result
    phiplusone=phi[:,1:141]
    phiplusone=np.insert(phiplusone,140,np.zeros(231),axis=1)
    phiplustwo=phiplusone[:,1:141]
    phiplustwo=np.insert(phiplustwo,140,np.zeros(231),axis=1)
    phimunusone=phi[:,0:140]
    phimunusone=np.insert(phimunusone,0,np.zeros(231),axis=1)
    phimunustwo=phimunusone[:,0:140]
    phimunustwo=np.insert(phimunustwo,0,np.zeros(231),axis=1)
    matrix+=(2*(phi-2*phiplusone+phiplustwo)-4*(phimunusone-2*phi+phiplusone)+2*(phimunustwo-2*phimunusone+phi)
    #This is to calculate the direvities of the regulizer
    phiplusone=phi[1:231,:]
    phiplusone=np.insert(phiplusone,230,np.zeros(141),axis=0)
    phiplustwo=phiplusone[1:231,:]
    phiplustwo=np.insert(phiplustwo,230,np.zeros(141),axis=0)
    phimunusone=phi[0:230,:]
    phimunusone=np.insert(phimunusone,0,np.zeros(141),axis=0)
    phimunustwo=phimunusone[0:230,:]
    phimunustwo=np.insert(phimunustwo,0,np.zeros(141),axis=0)
    matrix+=2*(phi-2*phiplusone+phiplustwo)-4*(phimunusone-2*phi+phiplusone)+2*(phimunustwo-2*phimunusone+phi)
    #This is to calculate the direvities of the regulizer
    for i in range(0,231):
        for j in range(0,141):
            result[141*i+j]=matrix[i][j]
    return result

• finally

import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
x=0*np.random.rand((231*141)) # the main variable of the total cost function, 231*141 indecates phi
x[426]=0.0001 # set one value tobe nonzero
x,min,info=scipy.optimize.fmin_l_bfgs_b(TotalCost,x,fprime=derivative,iprint=100) # bfgs method
phi=np.ones((231,141)) # regain phis
for i in range(0,231):
    for j in range(0,141):
        phi[i][j]=x[131*i+j]
plt.imshow(phi) # show the result
plt.colorbar()
plt.axis()
plt.show()
print(np.sqrt(np.sum(d**2)/(231*141)))

• And also we can check if the derivatives are right:

x0=np.random.rand((231*141+4*(end-start)))
diff=np.zeros((231,141))
difference=(derivative(x0))/(scipy.optimize.approx_fprime(x0,TotalCost,0.000001))-1
for i in range(0,231):
    for j in range(0,141):
        diff[i][j]=difference[141*i+j]
diff[diff>1]=1
diff[diff<-1]=1
plt.imshow(diff)
plt.colorbar()
plt.axis()
plt.show()

PROBLEM:

• The error of the derivatives:
  
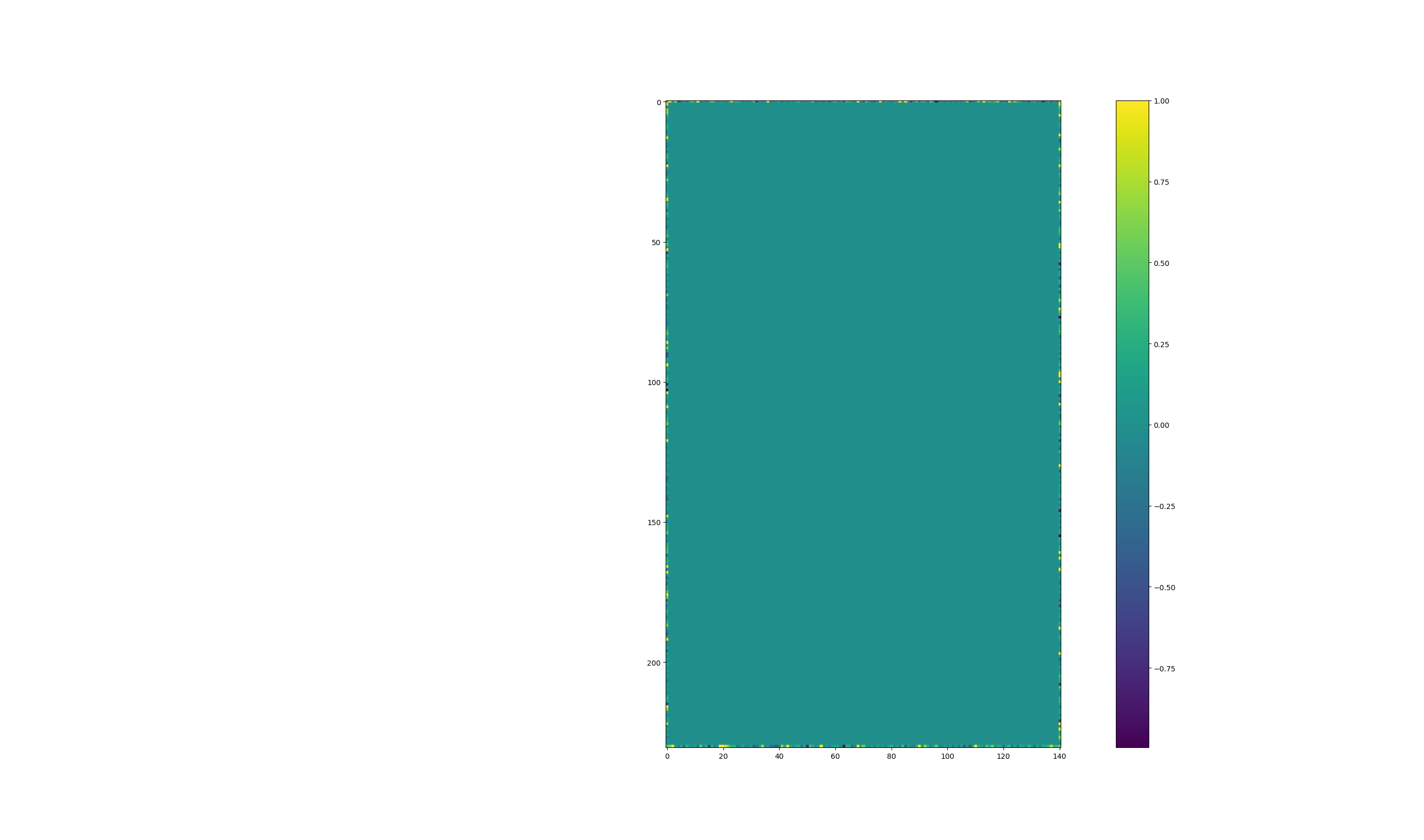
• initial to be all zeros:
  
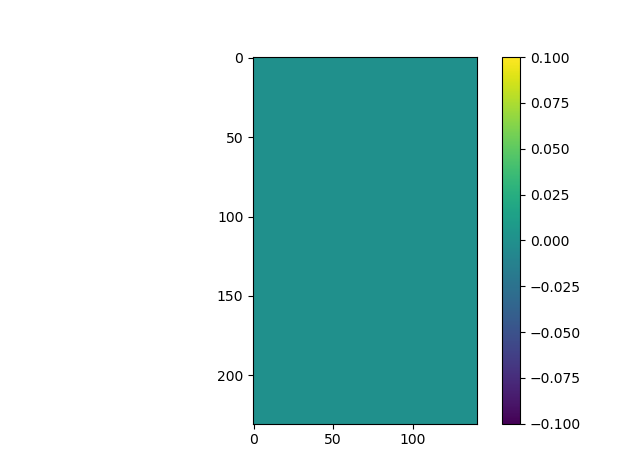
• a tiny diviation:
  
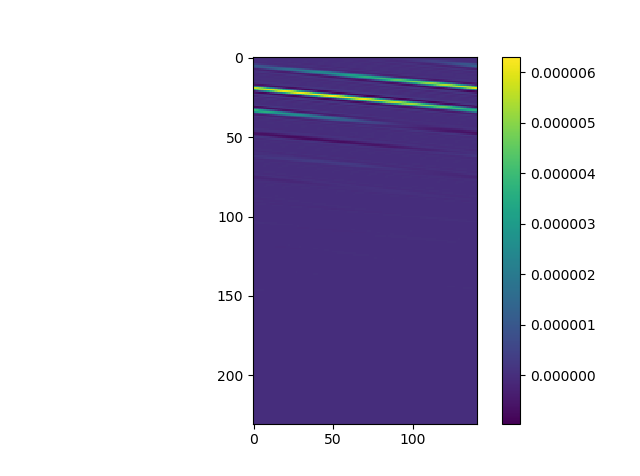
• This is hard to understand because obviously the flatter the plain is the smaller the derivatives are. And seems that the stripes are always orianted in this direction
• Is it possible to solve it better?