Vibration, Waves, and the Physics of Musical Instruments

python.assignment

---

姓名	学号	班级	选题	论述	结论
李芳莹	2013301020027	材料物理	研究乐器的弦上波的传播，以及弦振动的频谱	以波动方程为基础，动画再现了波的反射、叠加、半波损失等现象；应用快速傅立叶变换研究吉他弦振动的频谱，分析了特定频率消失的原因	波的传播满足叠加原理；波从光疏介质入射到光密介质时会发生半波损失；初始波包的对称性会导致特定频率的高频分量被抑制；当激发位于接近弦的端点处时，更多能量会被高频分量携带

I Abstract

Musical instrument utilize vibration and wave motion in different ways, this article consider several spcefic topics about wave and vibration on string. To be beginning, we investigate wave motion on a perfectly flexible, frictionless string, then we go to the power spectrum of a particular instrument, for example, guitar. Some interesting phenomena will be observed such as decomposition of wave package, generation of harmonics, frequency vanish and so on.

II Various phenomena of wave motion on a guitar string

The central equation of wave motion is

$$\frac{\partial^2 y }{\partial t^2}=c^2\frac{\partial^2 y}{\partial x^2}$$
This equation can be applyed to many situation, including electronmagnetic waves, waves on water surfuce, sound waves and so on.
We start with the simplest wave, the wave on a string which is fixed on the both ends. Even when this is a simple simulation, it can reveal many essential properties of waves, such as transmition, refection, half loss and superposition principle.

Nummerical Approach

We treat both $x$ and $t$ as discrete variables with $x=i\Delta x$ and $t=n\Delta t$, the wave equation can be written as finite difference form, for example,

$$\frac{\partial y^2}{\partial t^2}=\frac{y(i,n+1)+y(i,n-1)-2y(i,n)}{(\Delta t)^2}$$
So the whole equation can transfer to $$y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2[y(i+1,n)+y(i-1,n)]$$
in which $r$ means $c\Delta t/\Delta x$.
Then we fix the both ends with $y(0,n)=y(M,n)=0$ for all time steps n, in which we apply a fixed boundary condition.

Data analysis

pluck on a string

At first, we simulate a wave on a perfectly flexible, frictionless string with fixed ends, which is a extremely simplified simulation for string on some instruments. The string is set with general parameters, which has a length of 1m and wave velocity is 300m/s, and we take $r=c\Delta t/\Delta x=1$:

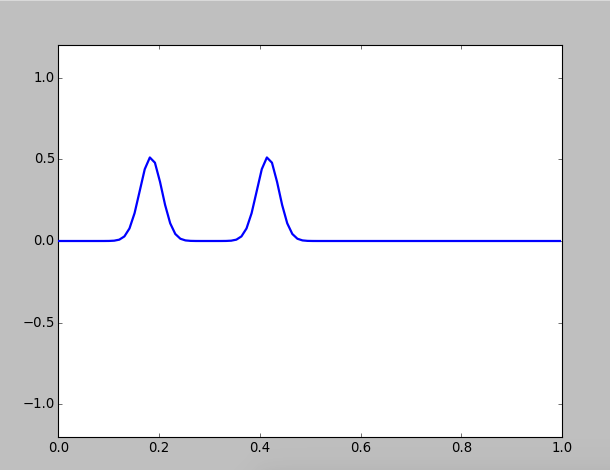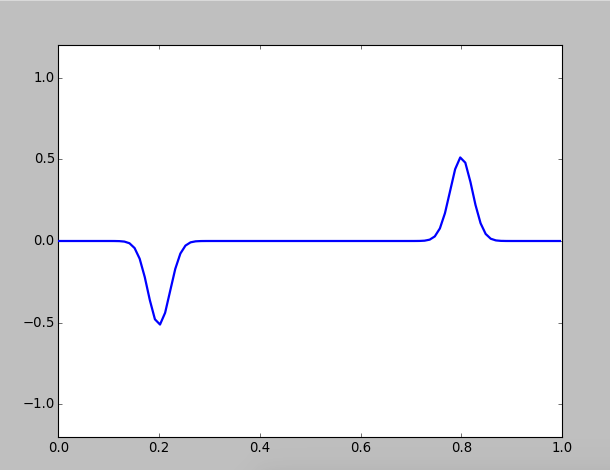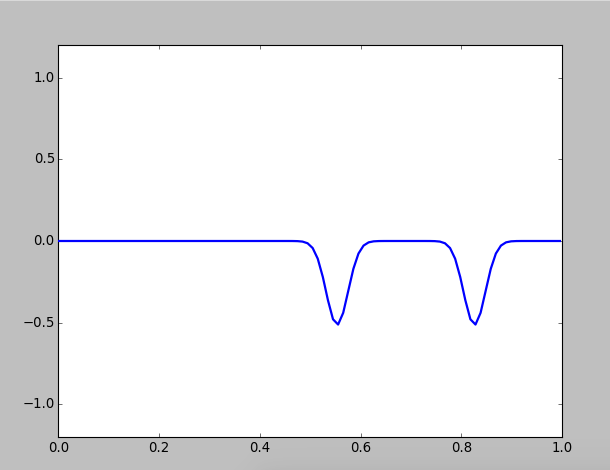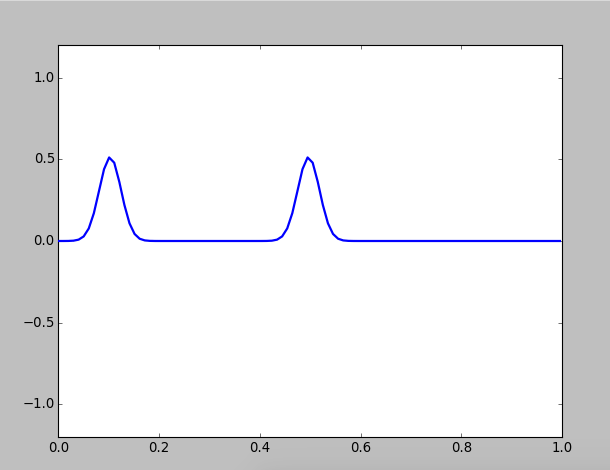
Figure 1: A pluck on a string with fixed ends
You can see a wave packet will automatically decomposes to two packets, and they propagate to opposite directions. What's more, when a wave packet reaches the end of the string, its vabrition direction will inverse.
In a specific instrument, for example, guitar, this wave package is called a "kink", which is stimulated by a pluck at the location. After the string is released, this kink splits into two separate kinks, which propagate towards opposite ends of the string. These kinks are reflected at the ends, and after one half of a period they reform as an inverted version of the origin pluck. This pattern continues, and after another half period the kinks inverse back.

superposition principle

Then we pluck twice at different location:

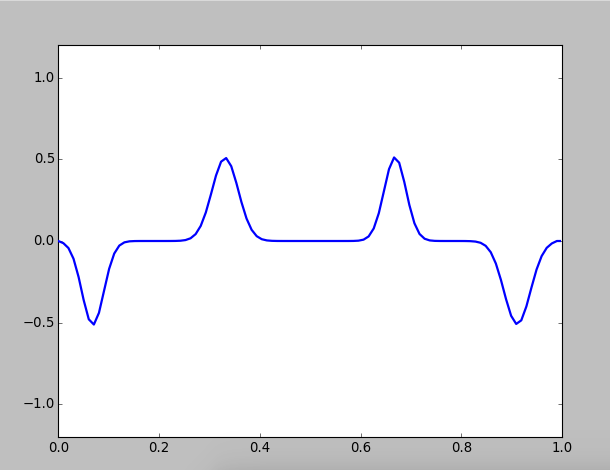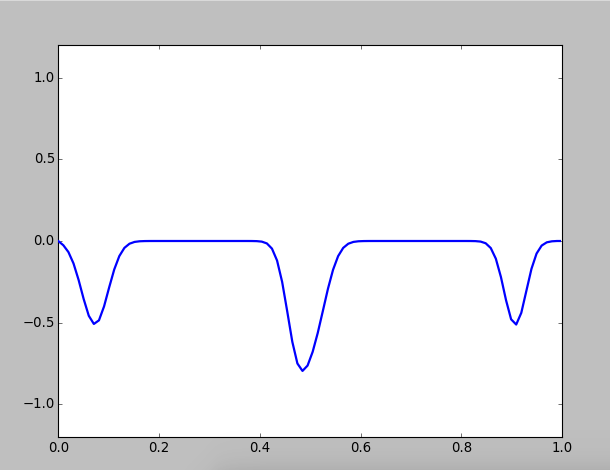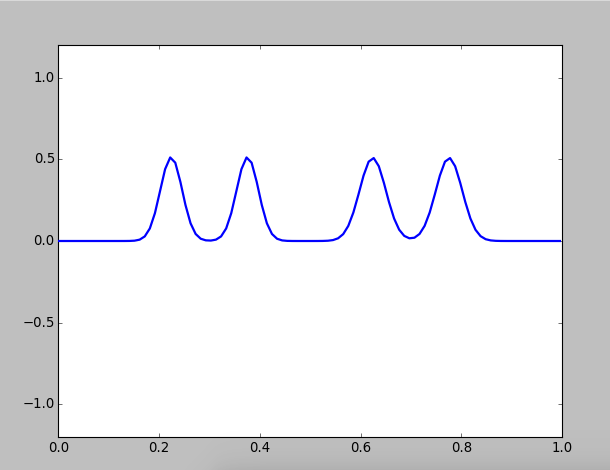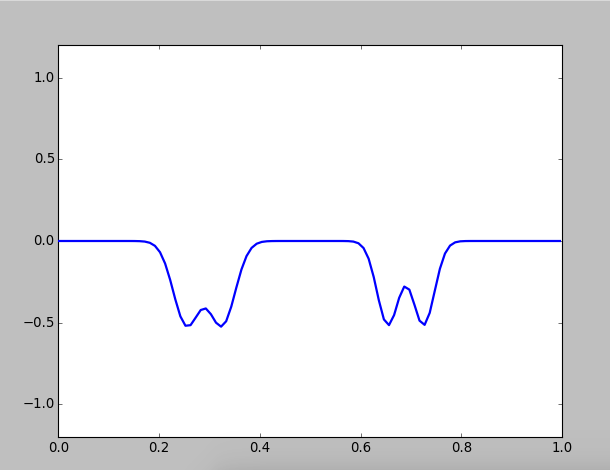
Figure 2: Pluck twice on different locations of a string
Two kinks will propagate towards each other and collide, but they are unaffected by each other, that's to said their shape and speed are unchanged. This result is reasonable beacuse the $wave$ $equation$ is linear, and all linear equations observe superposition principle.

half loss

Let's consider wave propagates on a composite string, transmits to a denser medium and reflects at the surface (even when composite string is not common in instrument, this situation is interesting to consider):

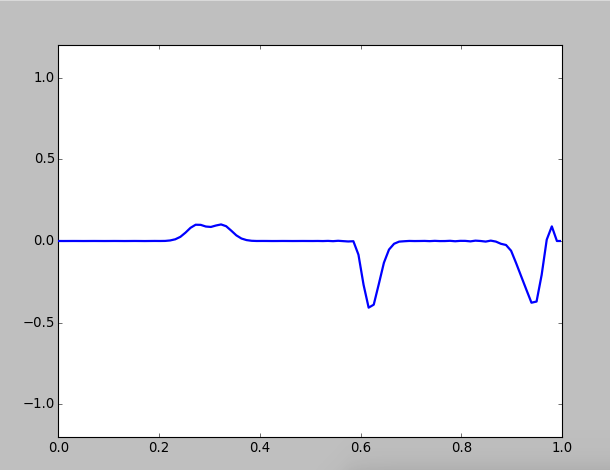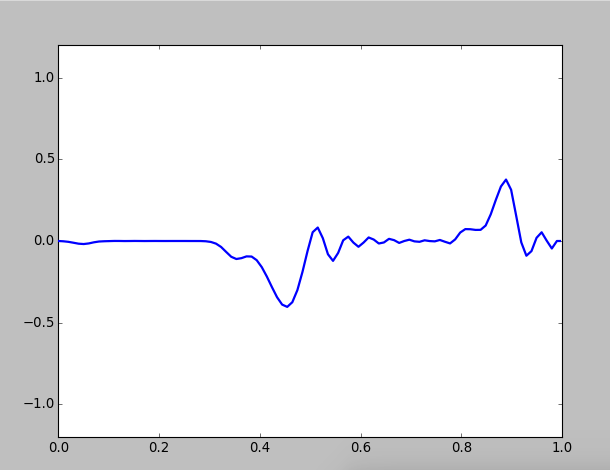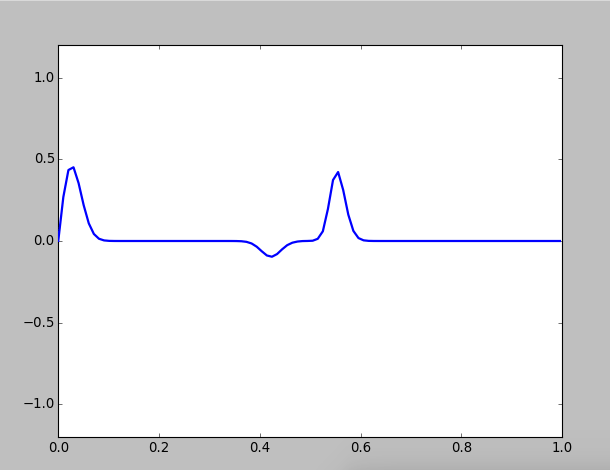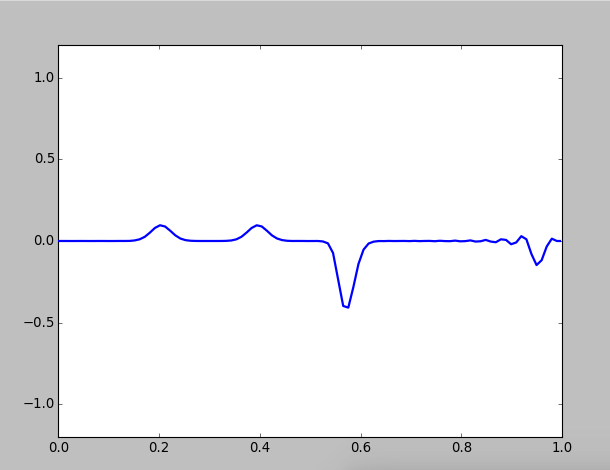
Figure 3: Wave motion on a composed string, with $c_1=300m/s$ in the first medium and $c_2=150m/s$ in the second medium

If we make the second medium even more denser:

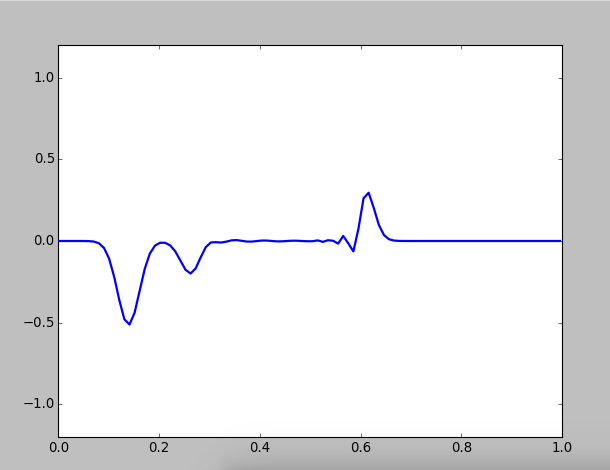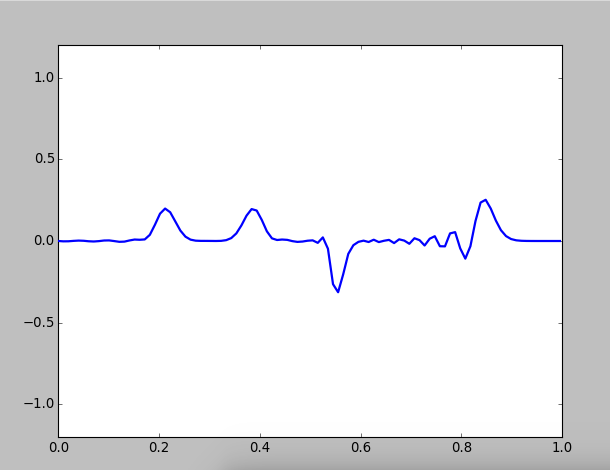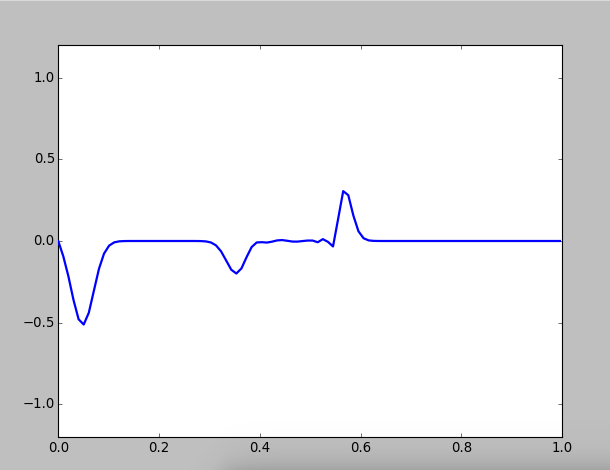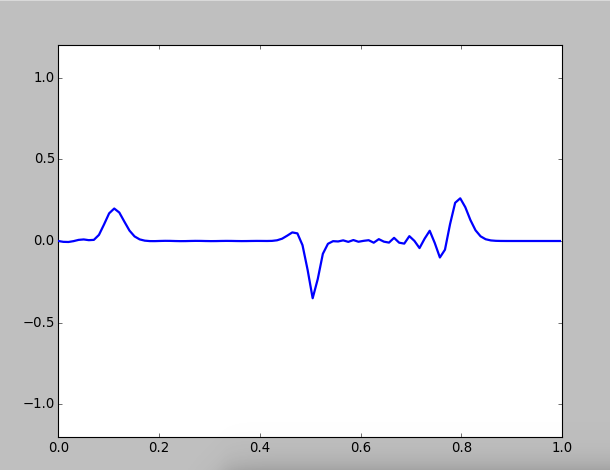
Figure 4: Wave motion on a composed string, with $c_2=125m/s$

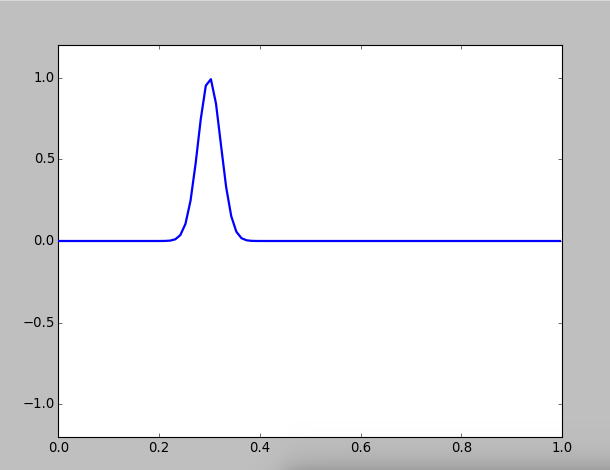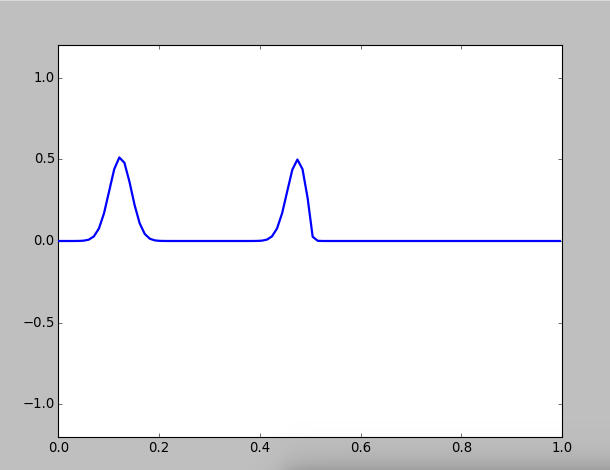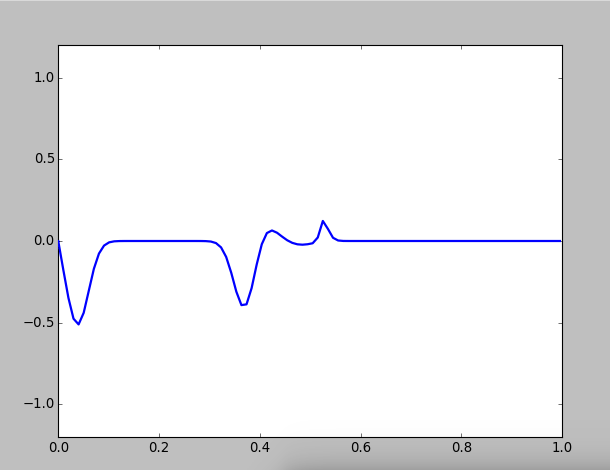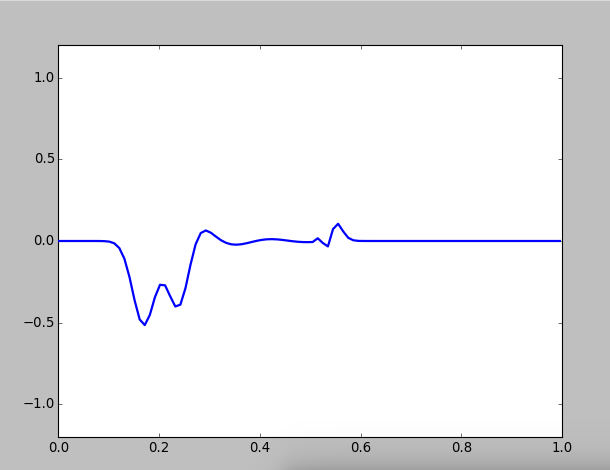
Figure 5: Wave on a composed string, when $c_2=15m/s$

When the second medium become denser, the amplitudes of transitted waves become smaller,and you can see the so-called half-loss phenomena:
because the incident angle is zero, when wave propagate from a sparse medium to a denser one, reflected wave has a phase mutation of $\pi$, which equals to half of the wave length of the opitical path is lost. So the vabrition direction of the reflected wave is changed, but the transmitted wave not.

Power spectrum of waves on a guitar string

Vibrating string are used in a variety of musical instrument, which makes it interesting to consider the frequency spectrum of waves on a string. At first we will start with a string with general parameters, than fix on a specific string of guitar.
Again we consider a string with fixed ends and not involve friction, the parameters are the same as above, but this time we consider a displacement at a particular point on the string as a function of time.
We pluck at the middle of the string and observe the vibration at $5$ $percent$ from one end:

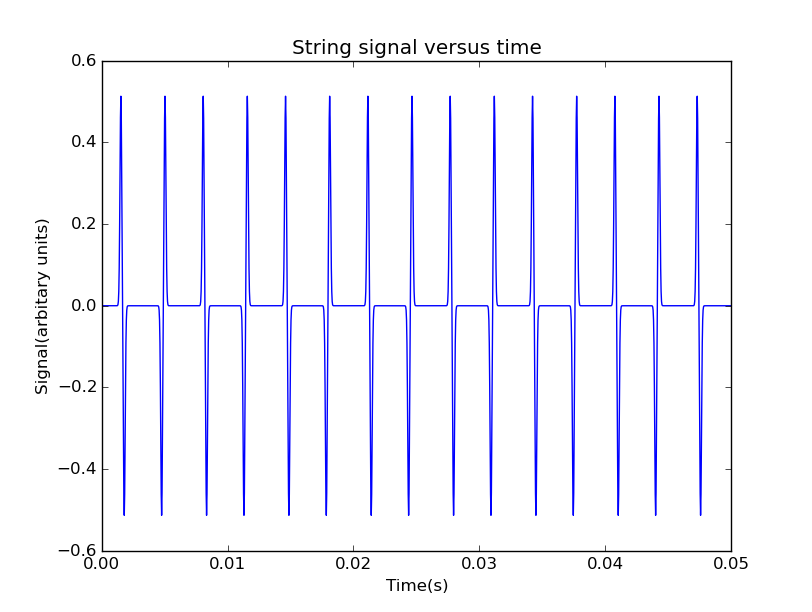
Figure 6: Signal from a vibration string which is excited at the middle, and the observation point is 5 percent from one end

We can see a series of pulse, each of which is produced when the wave packet move through the observation point.The pulse alternate in sign, that's because the wave inverted after it reflected at ends.
Furthermore, we can decompose this signal into Fourier components and display they in power spectrum:

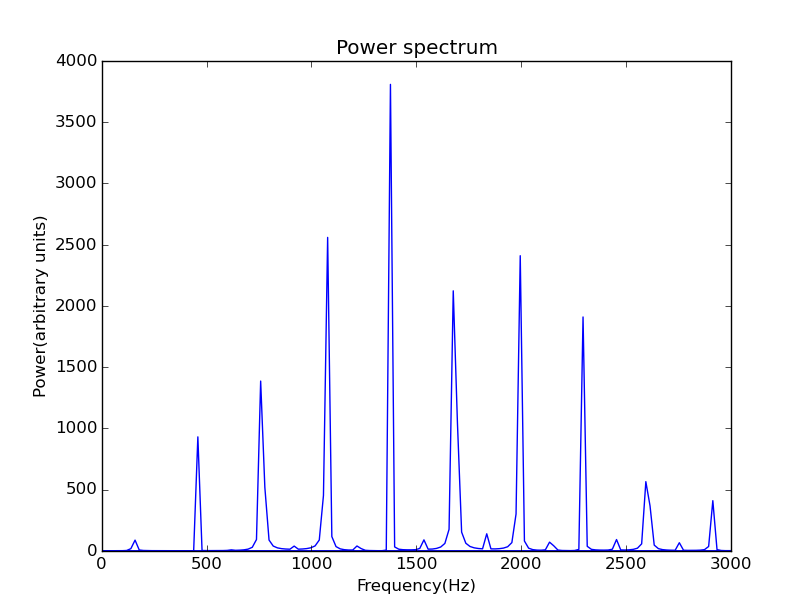
Figure 7: Power spectrum of the signal in figure 6. The initial pluck is at the middle of the string.

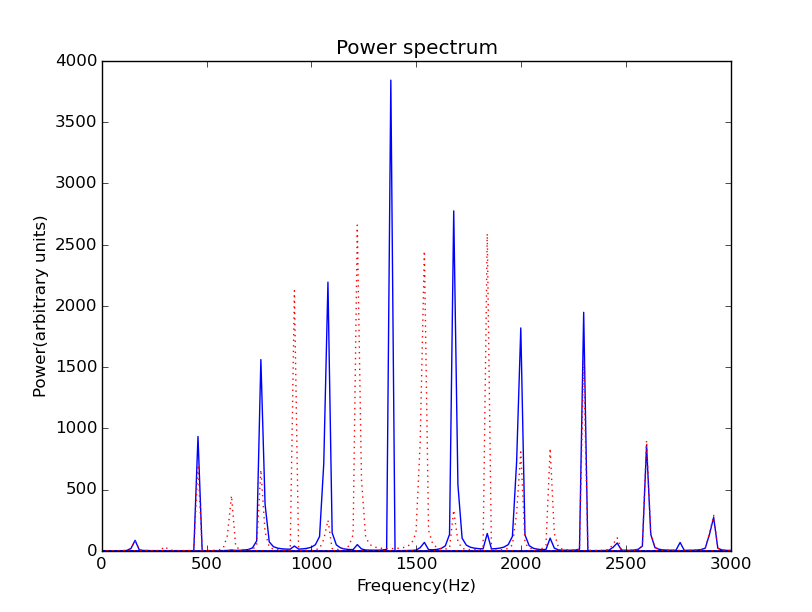
Figure 8: Power spectrum with the initial pluck 0.5 percent drifted from the middle (red dotted lines) and the original spectrum (blue solid lines)

As you can see, there are many peaks at particular frequencies, which can be understood as a series of standing waves with their own frequencies. And a slight difference of the initial pluck point will cause the whole spectrum translation for a certain distance.
These standing waves are so-called the basic spatial Fourier components of the string vibration. Each of these standing waves has a specific wavelength $\lambda=2L/m$, where $m$ is an integer, so the possible frequencies are $mc/2L$.For the parameters we take, the fundamental frequency is $c/2L=150Hz$,and obsering the peaks in figure 7, you can find out that there are only peaks at odd times of fundamental frequency, like $450Hz,750Hz, 1050Hz...$and the even times frequencies are all vanish.
To explain this phenomenon we need to consider how the string is plucked, that is, where the initial wave packet is set. Our wave packet is located at the middle of the string, so it is symmetric with respect to the center. We should pay attention to Fourier transform will preserve the symmetry of the signal when it transform from time domain to frequency domain, so the preserved components will be those that are nonzero at the middle of the string. That's to say, those components have nodes(节点)at the middle, with frequencies $f=cn/L=2n*c/2L$ will vanish. To conclude, the argument is the symmetry of the initial wave packet can cause certain frequencies be suppressed.
The lowest frequency is referred to the frequency of the note(音符), and high frequency components are so-called harmonics. Even though the frequency of a note is all the same in different instruments, we are not hard to distinguish a piano from a violin, that's because each instrument produce a distinctive pattern of harmonic components. The relative strength of harmonics and how they change with time is vary from instrument to instrument.
Next we relate this phenomenon to specific instrument, for example, guitar.
We have to set the parameters especially for guitar. $B$ $string$ of a guitar has length of $L=0.65m$ and wave velocity $c=320m/s$. We pluck at $L/5$ from one end, and observe the vibration at $L/5$, too:

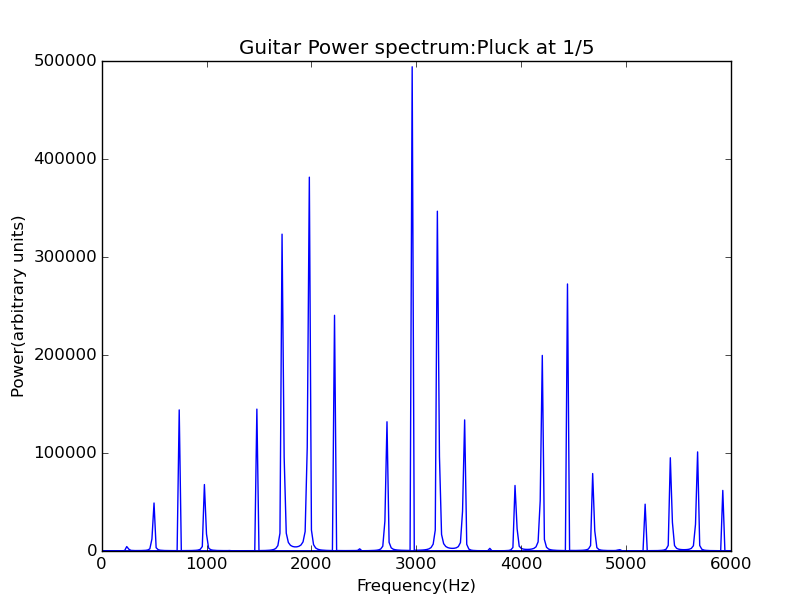
Figure 9: guitar spectrum with a initial pluck at L/5

Have our previous analyse in mind, the phenomenon is not surprising. Harmonic components which have nodes at pluck point are vanished, for this problem the node is $L/5$ from one end, so components with $\lambda=2L/5n,f=5n*c/2L$ will vanish. Observe the figure, you will find $f=5,10,15,20f_0...$ missed.
Next step we excited the string at $L/20$ from one end:

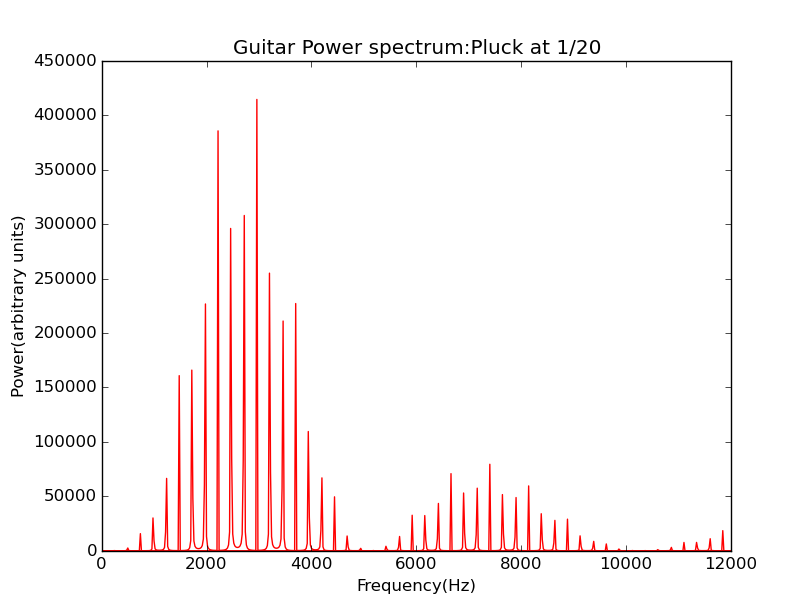
Figure 10: guitar spectrum with a initial pluck at L/20

What's the difference? We notice that the component at $f=20,40,60f_0...$ vanish, and more importance, the magnitude of the harmonics decrease much slowly as frequency rise, that's means much more of the sound power is carried by the harmonics. This is why we pluck very close to one end of the string, the guitar give out a sound "twang".

III Conclusion

In the first part we simulate wave packages propagate on flexible, frictionless uniform string and composite string, and observe packages decomposition, reflection and inversion. Then we verify superposition principle of waves and we also analyse half loss phenomenon. Although the model is simple, it reveals many intrinsic properties of waves.
Then we find out the symmetry of the initial wave packet can cause certain frequencies be supressed, and we confirm it by simulating the vibration of guitar string.
Third, we find that the closer initial wavepacket set to the end of the string, the more energy carried by harmonics components.

program codes

wave.py
guitar_sp.py

Acknowledgement

Thank HeChong for patient direction^^

Reference

Nicholas J.Giordano, Hisao Nakanishi. 2007. Computational Physics[M]. Beijing: Tsinghua University Press