Chapter 1 problem 1.5

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

This is a programme to describe the evolution of a system that can move back and forth between two states, likes a resonance.The problem is solved by Euler method and results are plotted and analysed.

Introduction

Consider a decay problem with two types of nuclei A and B which can decay to each other.The corresponding rate equations are

$$\frac{dN_A}{dt}=\frac{dN_B}{\tau}-\frac{dN_A}{\tau}$$
$$\frac{dN_B}{dt}=\frac{dN_A}{\tau}-\frac{dN_A}{\tau}$$
Two types of decay are characterized by the same time constant, $\tau$. And $N_A$,$N_B$ are the number of nuclei, as functions of time.
The system will reaches a steady state in which the number of nuclei are constant as show in follow.

The Nummerical Approach

In mathematics and computational science, the Euler method is a SN-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value.
It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method.
The essence of Euler method is this taylor expansion:

$$N(t+\Delta t)\approx N+\frac{dN}{dt}\Delta t$$
we use the right hand of the equation as the approximation of left hand and the solution of a ODE at time: t+$\Delta t$.
For more information, wikipedia gives a detailed describe: Euler_method.

Result and analysis

In the program, the initial number of A is 100 and that of B is 0. Change the time constant $\tau$ , dt and total time, you can get different results.

In the following pictures, the green and blue line describe the realistic change of the nuclei A and B as functions of time,which are analytic results. And the dotted lines reflect the relvolution of A 2 B by numerical method.

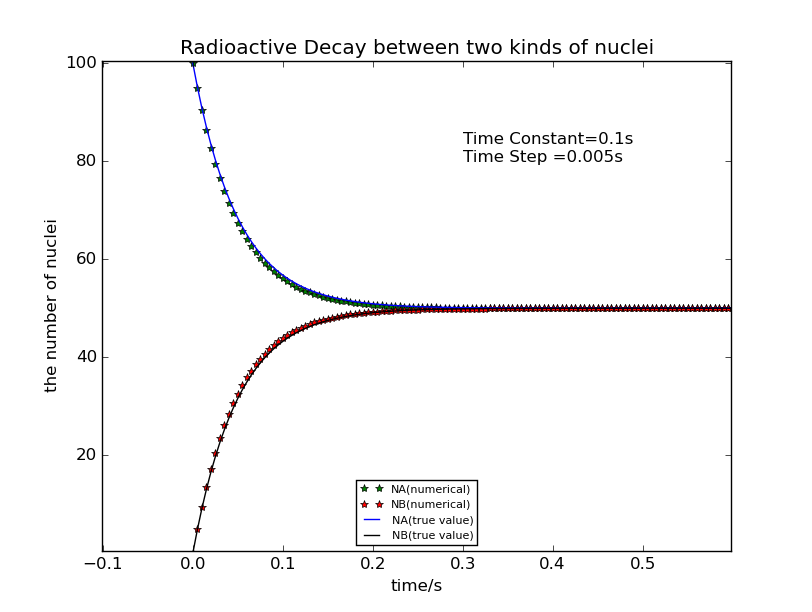
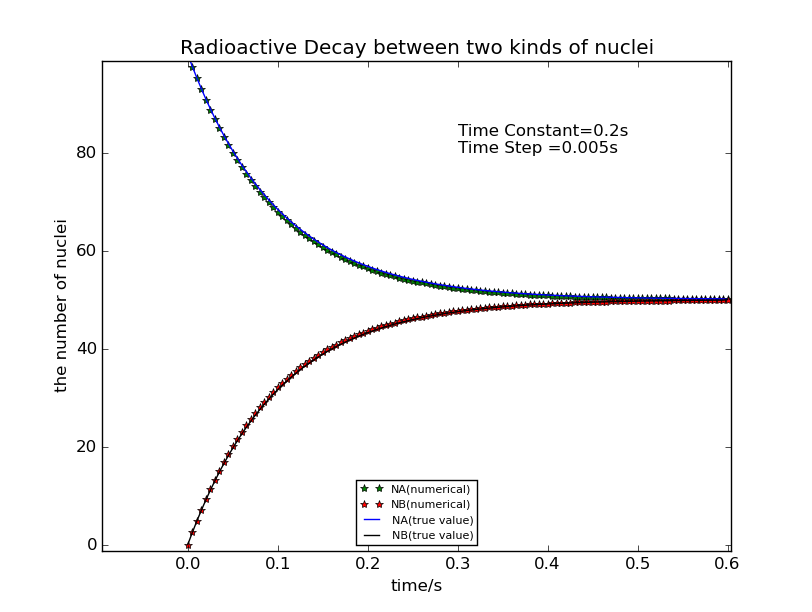
Not all $\tau$, dt and total time can get proper results.You should choose the value carefully.
As you can see, when the time constant $\tau$ get larger, the decay turn slower. And the numerical values fit quite well with the analytic ones.

Conclusion

A program is written to describe a system with two nuclei decay to each other,in this project, Euler method is used to solve a system can be described by simple first order ODEs.
Besides, all the high order ODEs can be transferred into first order ones, so Euler method can also be applyed to high order ODE.

program codes

the program of problem 1.5