Chapter 3 problem 3.8

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

Introduction

The studying of simple pendulum has a long history. In 1583, Galileo discovered the isochronism of a pendulum when he was 17, that is , the period of a pendulum is independent of its amplitude. This great discovery was applied to pendulum clocks, which still exist in our lives after hundreds of years.

But in 1656, Huygens noticed that the isochronism principle has a limit. The initial angle $\theta$ must small enough, no more than $10^{\circ}$ for example, to make the approximation $sin\theta\approx\theta$ correct. What's about larger $\theta?$
Next, advantages of both analytic approach and numerical approach will be taken to answer this question.

Analytical Approach

The ODE of simple pendulum without approximation can be write as:

We can set the angular velocity as $w$,and the equation turns to:

Transform it:

Integrate it:

If we set innitial value $\theta=\alpha$ and $w=0$, we get:

The $\frac{T}{4}$ can be expressed as:

So finally we get the analytical solution of this ODE:

Numerical Approach

The ODE equation of nonlinear pendulum is

$$\frac{d^2\theta}{dt^2}+g\sin\theta/l=0$$ can be transfer to two one-order ODEs: $$\frac{d\theta}{dt}=w,\frac{dw}{dt}=-g\sin\theta/l$$ And the equation for numerical calculation are: $$w_{i+1}=w_i-g\sin\theta_idt/l$$ $$\theta_{i+1}=\theta_i+w_{i+1}dt$$
where we use Euler Cromer method. It has a minor change compared to Euler method, which will accumulate deviations towards one direction for problems involving oscillatory motion, this method can conserve energy over each complete period of the motion. So, it's a much better choice.

Data analysis

Set pendulum length as $l=1.0m$, $g=9.8N/kg$ and intial angular speed as $w=1.0rad/s$.
When $\theta$ is less than $10^{\circ}$, the linear and nonlinear pendulum has minor difference:

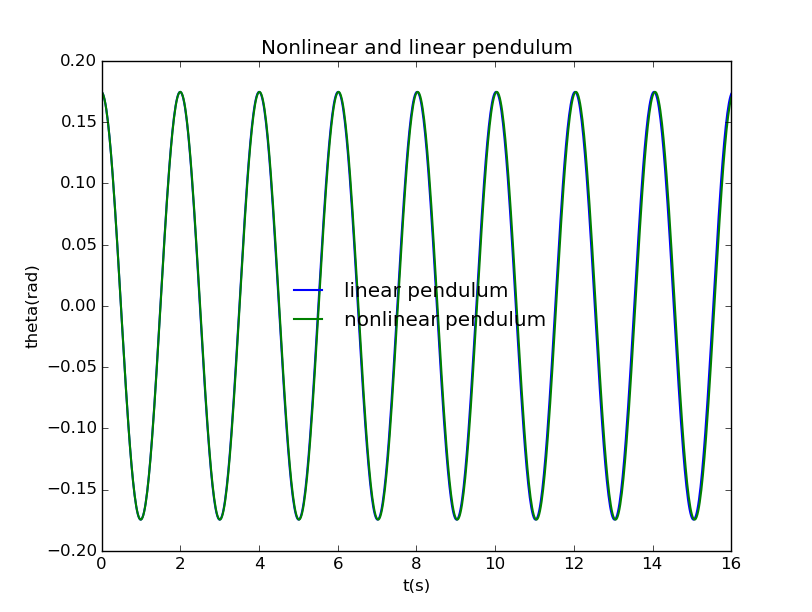
That is to say, the equation $sin\theta\approx\theta$ is proper.
But when we raise the initial angle to $15^{\circ}$, thing becomes a little interesting:

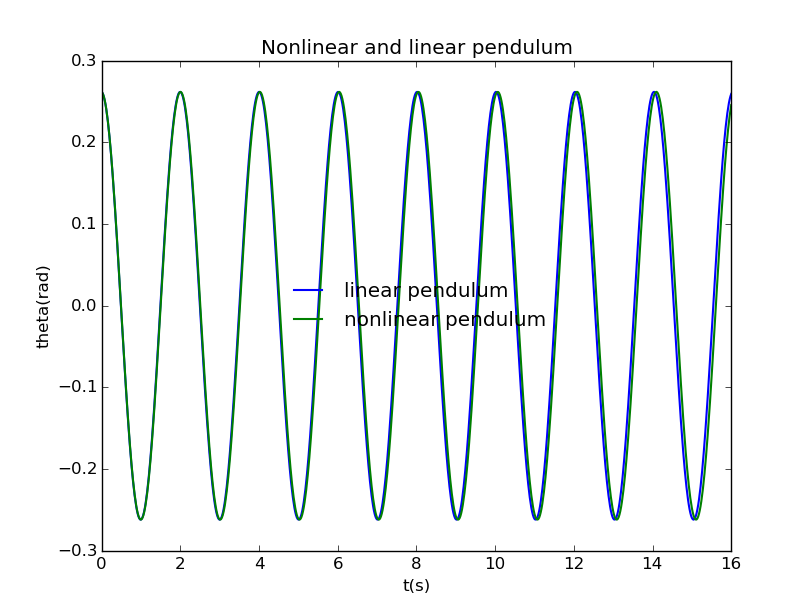
When we change the intial angle to $40^{\circ}$:

$\theta=80^{\circ}$

$\theta=160^{\circ}$

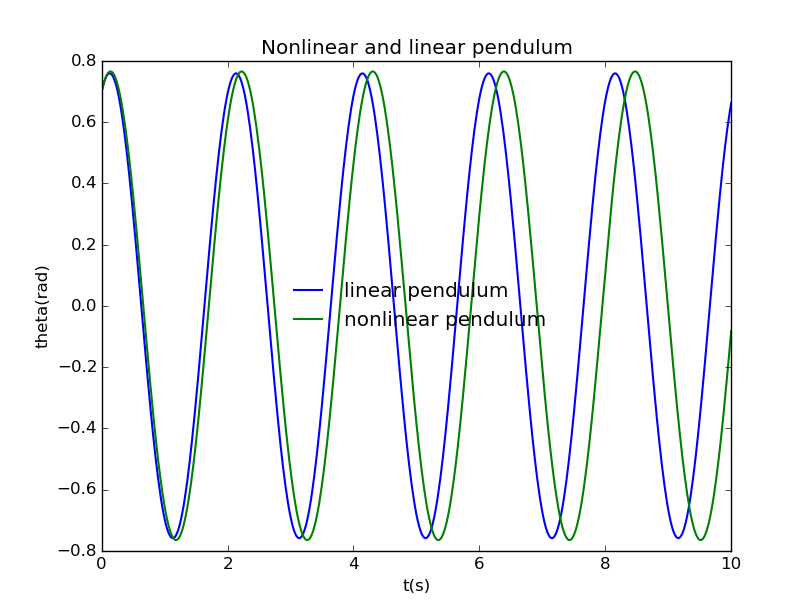
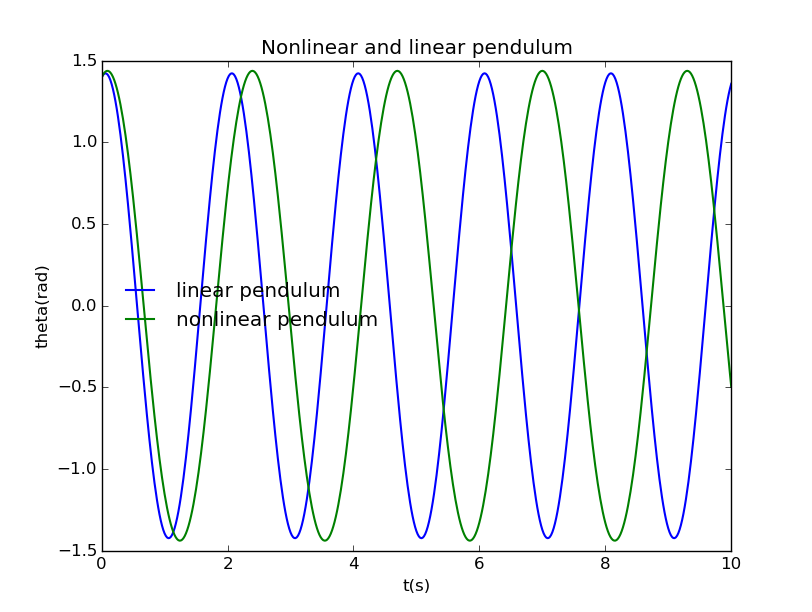
As the initial agnle raises, the period of nonlinear pendulum grows larger and larger, and when it arounds $160^{\circ}$, the period becomes penculiar:

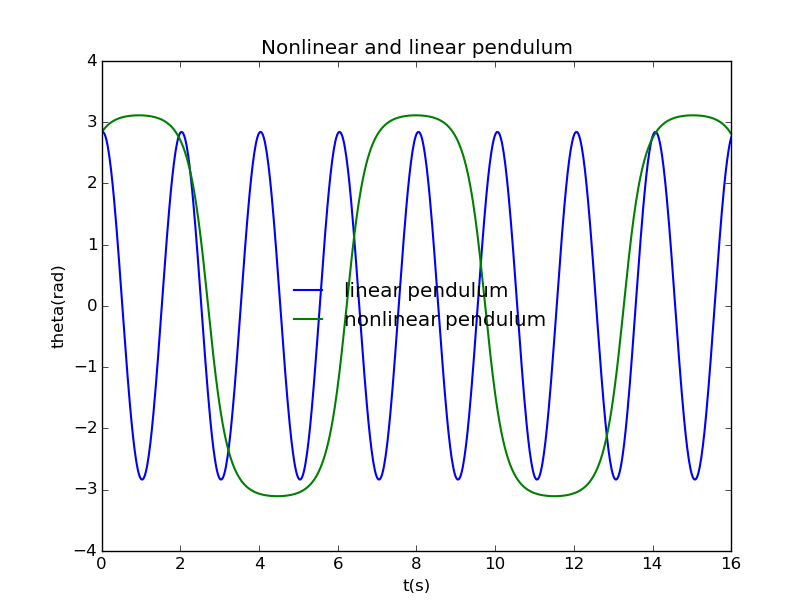
When we raise the angle a little more, something surprising happen:

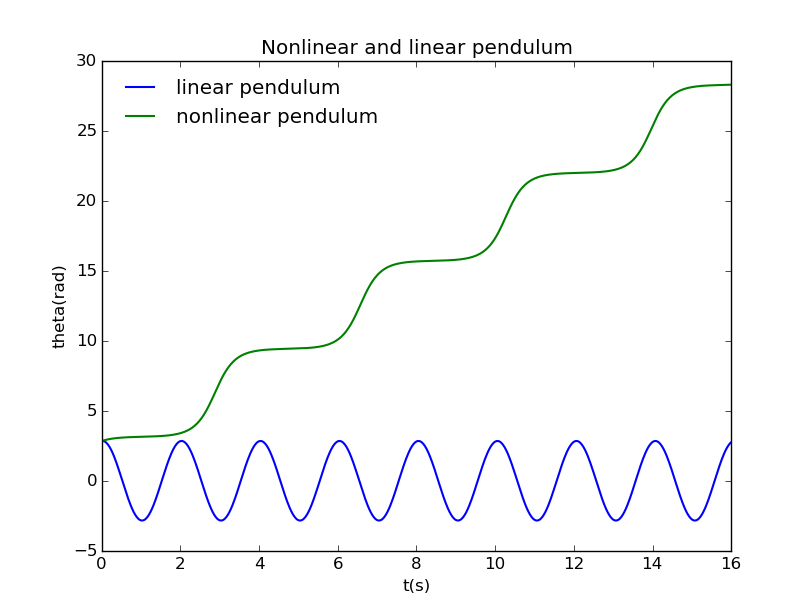
the turning point is between$162.10$ to $162.15$, just $0.05^{\circ}$makes big difference$!$
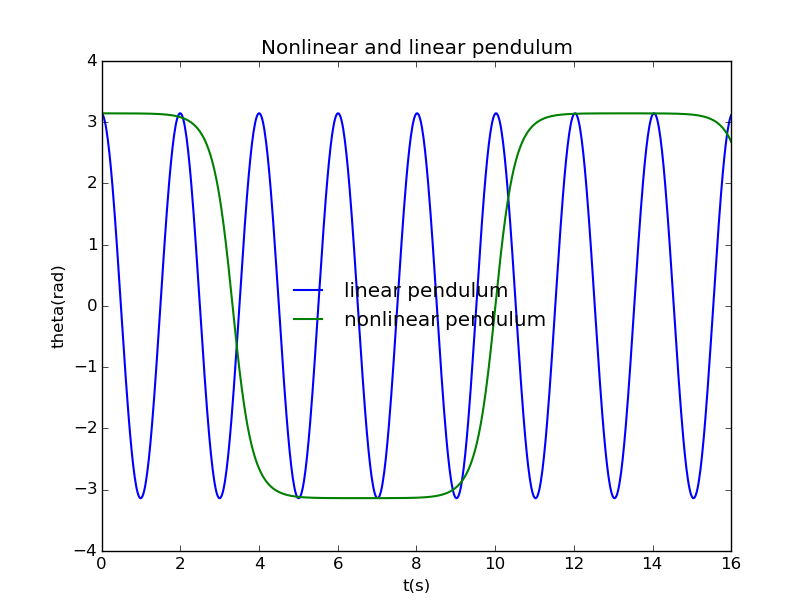
Notice, the initial angular speed is $1.0rad/s$ now, if we change it, the turning point will change,too. For example, if the initial angular speed is $0$, the turning point will not appear:
When $\theta=180^{\circ}$:

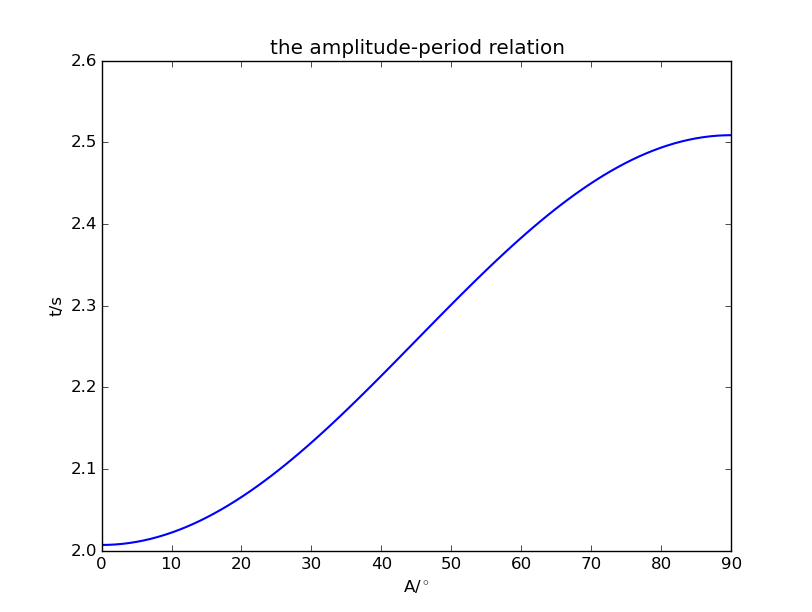
If we plot the relation of period and amplitude, it will be:

Conclusion

Analytical solution of a nonlinear pendulum is given as well as numerical approach.
The $t-\theta$ figures are plotted to compare the period of linear and nonlinear pendulum at different initial angle.
The turning point of the paranoral phenomena is fixed at a accuracy of $0.05^{\circ}$. Moreover, the variation of the turning point by different initial angular speed $w$ is observed.
And the $A-t$ figure shows the period of nonlinear pendulum is raising when amplitude increases, and their relation is nonlinear.

program codes

pendulum.py