Chapter 1 problem 1.3

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

This is a programme to describe the velocity of a parachute.The problem is solved by Euler method and results are plotted and analysed.

Introduction

As you know, the role of a parachute is to produce a frictional force due to air drag, this force will increase as the object move faster. Consider a simple condition that the frictional force depends on velocity.
Assume that the velocity of a object obeys an equation:

$$\frac{dv}{dt}=a-bv$$
where a and b are constants. a comes from gravity and b raises from the frictional force. In the following the velocity evolution of a parachute accroding to this equation will be analysed by Euler method.

Nummerical Approach

In mathematics and computational science, the Euler method is a SN-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value.
It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method.
The Euler method is named after Leonhard Euler, who treated it in his book Institutionum calculi integralis.
The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size. The Euler method often serves as the basis to construct more complex methods, e.g. Predictor–corrector method.
For more information, you can visit Euler method.

Results Analysis

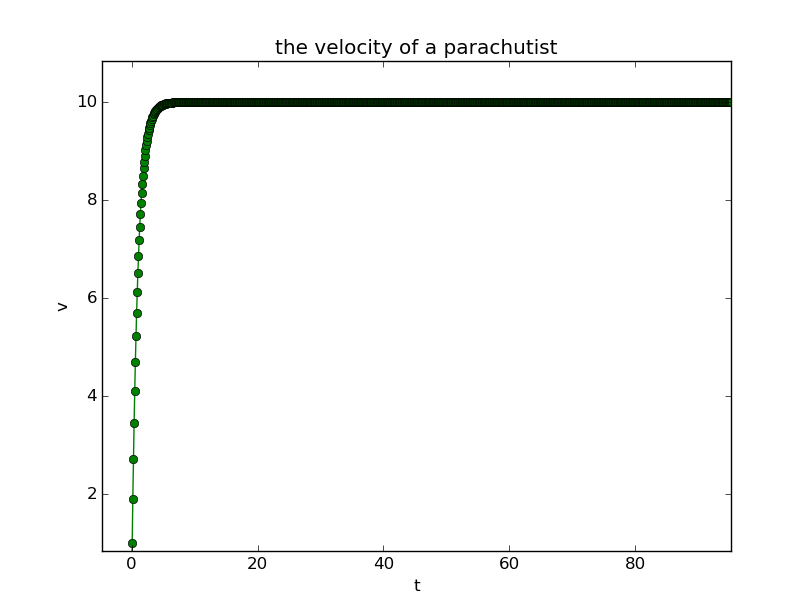
As the result shows, the velocity will reach a constant as time goes by. Thanks to the frictional force, the $(- bv)$ term, we can carry a parachute and jump from a plane with hope to survive.
In the picture above, I set a=10 and b=1, if you change the constant b, for example, make it larger, you will find the time the system consumes to reach equibalance will become shorter.

Conclusion

Program is written to describe the velocity change of a parachute, and you will find out that the velocity approaches to a constant as time goes by due to the frictional force.
In this project, Euler method is used to solve a system can be described by simple first order ODEs.
Besides, all the high order ODEs can be transferred into first order ones, so Euler method can also be applyed to high order ODE.

program codes

The code is really simple, my first program^_^