Chapter 1 problem 2.19

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

The game of baseball has fascinated fans of the game, and also physicists for many years. That's because many interesting phenomena will come into being after a hit. Our goal this section is to take the effect of atmosphere drag and the spin of ball into account, finding out how far a real baseball should be expected travel when hit by a typical power hitter.

Introduction

To treat the problem of a thrown ball, we must deal with two different effects: the spin of the ball, this will turn out to dominate the motion of a curve ball; the other effect concerns the difference in the drag coefficient for rough and smooth balls, and this will be crucial for the behavior of a knuckleball.

the effect of air resistance

Just like many other macroscopic object travel throught atmosphere, air drag have a key influence on the trajectory of baseball, the force on a baseball due to air resistance is given by:

$$F_{drag}\approx-1/2C\rho A v^2$$
And the coefficient $C$ is actually a strong function of $v$, as speed increase, $C$ drops substantially. Because at high speed the air follow around ball becomes turbulent, and the drag coefficient for rough, normal and smooth ball is different.
For our numerical work it's convenient to have an analytical representation of $C$, the drag factor is described well by this function: $$\frac{B2}{m}=0.0039+\frac{0.0058}{1+exp[(v-v_d)/\delta]}$$
with $v_d=35 m/s$ and $\delta=5 m/s$. Using this parameterization of the drag we can construct a program to calculate the trajectory of baseball.

the effect of spin

Because of the spin, the edge of the baseball at the bottom will have a larger velocity relative to the air than the top. This will result in a larger drag force edge of the ball where the velocity is highest than on the opposite edge, which due to the curved force of the ball it has a component that is directed towards the top or the bottom. When the force on the two sides of the ball added, there will be a net force, which known as Magnus force. Tt is believed to make an important contribution for objects such as baseball.

$$F_{Magnus}=S_0(w\times v)$$

For ore information about Magnus force, click Mangus force-wikipedia

Numerical Approach

Again, Euler method is applyed to solve this problem.
The equation of motion for a sidearm curve ball are($x$ is the axis running from home plate to the pitcher, y is the height above the ground :

$$\frac{dx}{dt}=v_x, \frac{dv_x}{dt}=-\frac{B_2}{m}vv_x-wv_yS_0$$ , $$\frac{dy}{dt}=v_y,\frac{dy}{dt}=-g-\frac{B_2}{m}vv_y+wv_xS_0$$

Data analysis

the maximum gap between ball with and without backspin

Three differnt initial speeds of the baseball are applyed on baseballs with and without spin. Typical results are shown below:

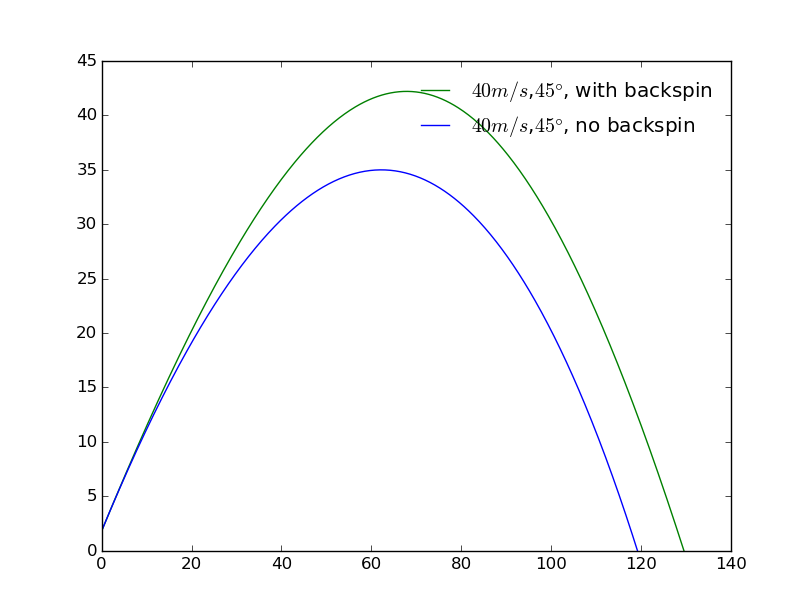
You can see that backspin indeed increases the maximum range.When $v=40m/s$, the maximum range of baseball without backspin is $119m$, while ball with spin is $129m$, $gap=129m-119m=10m$.
When we raise the initial speed to $50m/s$:

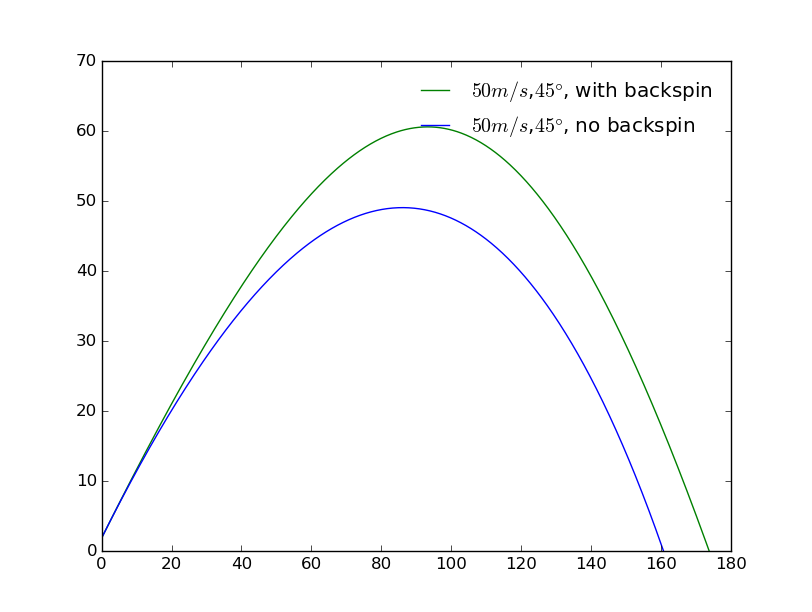
The trajectory change and the gap between two maximum range increases. $gap=173m-160m=13m$
When we raise the initial speed to $60m/s$:

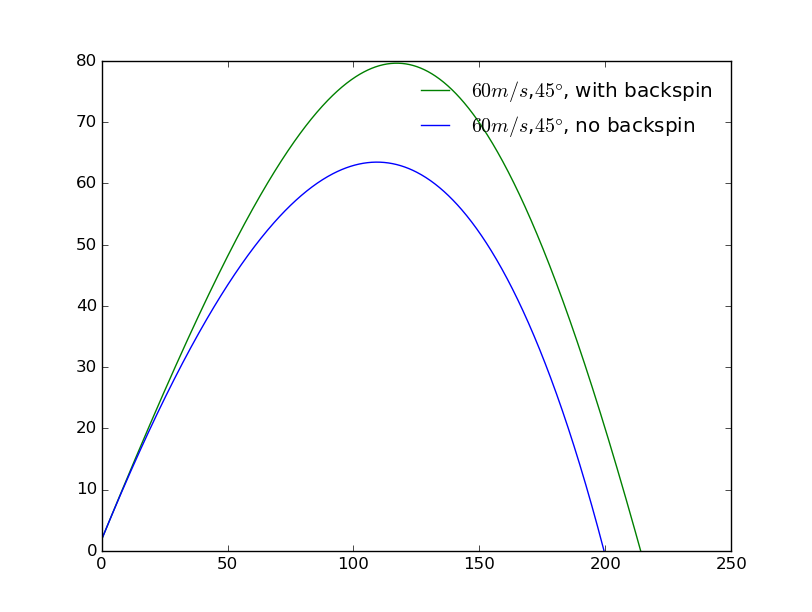
The gap turns to be smaller, their $gap=214m-199m=15m$
As the initial speed increase, the gap between baseballs with and without spin probably first increase then decrease.
Some may think the larger initial speed will cause the larger gap, but when $v_0=100m$:

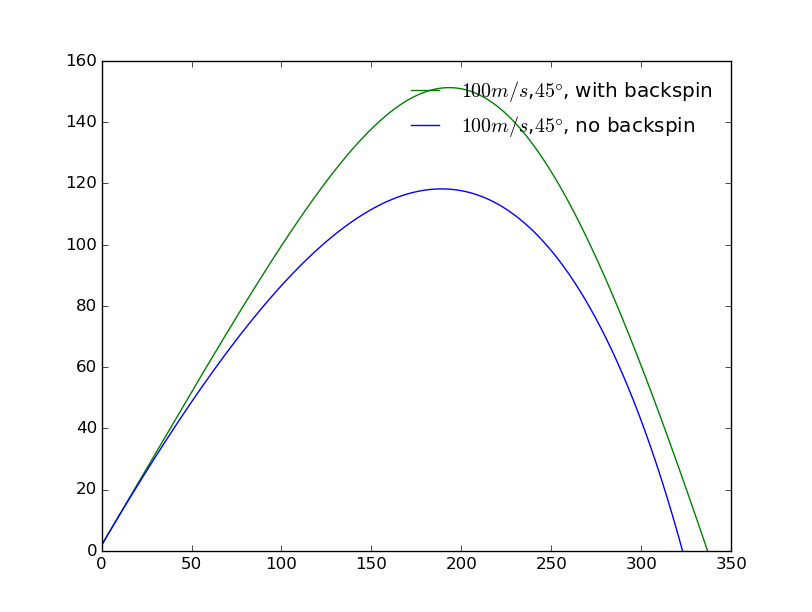
The $gap=336-322=14m$ ,it actually decreases. Besides, in the real world we cannot throw a baseball that fast.
the maximum gap may appear when the initial speed around $50 m/s$.

the maximum range at different initial angle

The discussion above is not very satisfactory because in reality no person can throw a baseball with the initial speed as high as $50m/s(180km/h)$. In general, a professional pitcher is capable of reaching $160km/h$, that is $41.6m/s$. To make the problem more realistic, we will continuw the discussion under the condition that the initial speed is the general speed $41.6m/s$.
We can consider different initial angles at this speed:

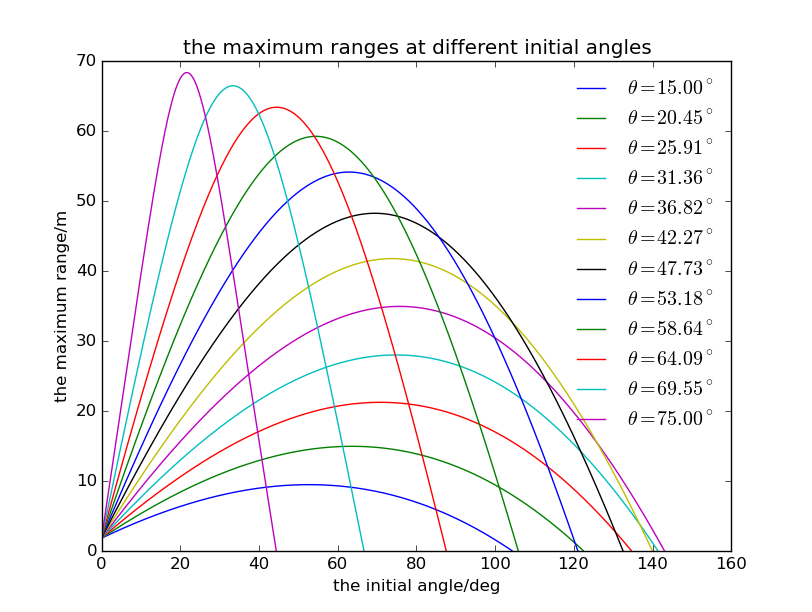
As you can see, the maximum range is reached when initial angle is $36.82^\circ$
If you are dizzy with these lines, this is more clear:

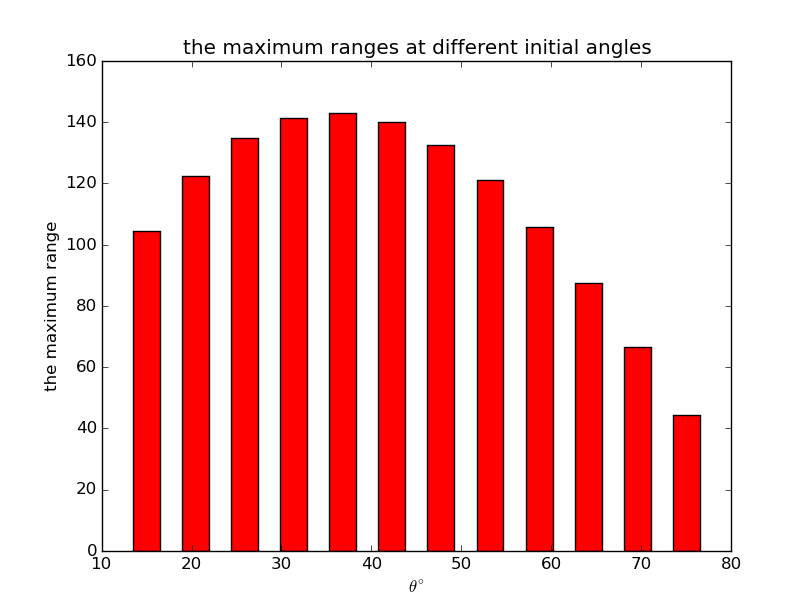
Conclusion

Airdrag can lead to the maximum range of a baseball decrease and backspin has the opposite effect, and the gap between baseball with spin and without spin is varies from different initial speed. When initial speed around 50m/s,the gap between two of them maximize.
What's more, when you consider a general speed baseball pitchers can reach, $41.6m/s$ as the initial speed, the maximum range is achieved when the initial launch angle is $36.8^\circ$ .

program codes

spinbaseball.py

THANKS

I should thank WangShixing (0145) for refering his program as a learning mode and GuoShuaifei (0066) for the plotting skill he taught me. Best wishes to you!