Chapter 5 problem 5.3

python.assignment

name: Li FangYing
number: 2013301020027

Abstract

Use Jacobi method to solve the potential and electric field inside a square box and between a plate capacitor whose plates are finite. Equipotential lines and electric field of these problems are shown in figures.

Nummerical Approach

$Relaxation$ $method$ is a useful way to deal with several classes of partial differential equation, such as $Laplace's equation$ and $diffusion$ $equation$, and $Jacobi$ $method$ is the simplest form in it.
The main idea of this method is to begin with a initial guess for the solution, and use it to calculate new values, until the result satisfies a convergence criteria. We will apply Jacobi method to tackle this problem.

Data analysis

Let's start with a simple problem of calculating the potential and electric field inside a box to test the feasibility of Jacobi method.
The face of the box at$x=-1$ is held as $V=-1$, while $V=+1$ at $x=+1$.
we assume that the sides of the box at $y=+1,-1$ are nonconducting, so V on these faces will vary as we moves from$x=-1$ to $x=+1$.
It's naturally to predict that the potential will vary linearly with the position, so let's test whether the Jacobi method give the reasonable result.
The equipotential lines acquired by Jacobi method is:

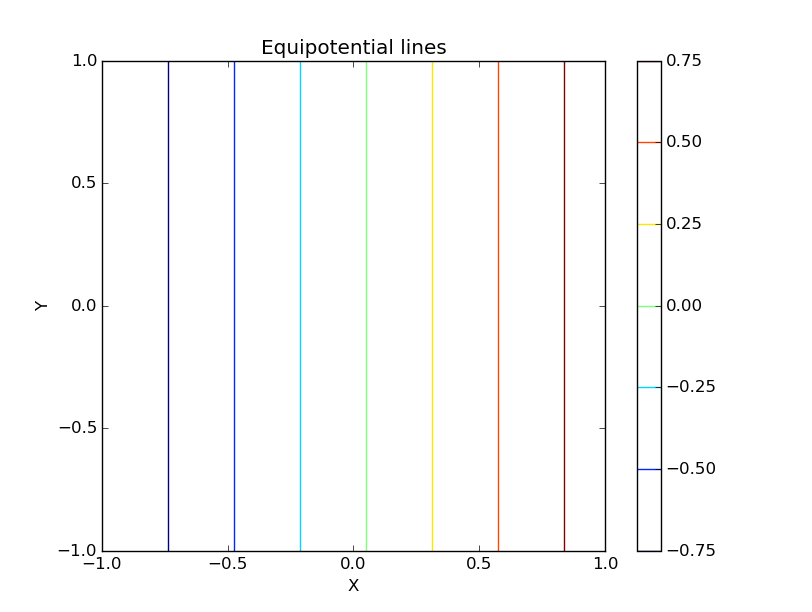
This is a contour map, and these contours are lines drawn thrown locations where potentials are particular value, which accords with what we have expected for this problem.
And we can also shown electric field between the two metal plates by a vector plot.

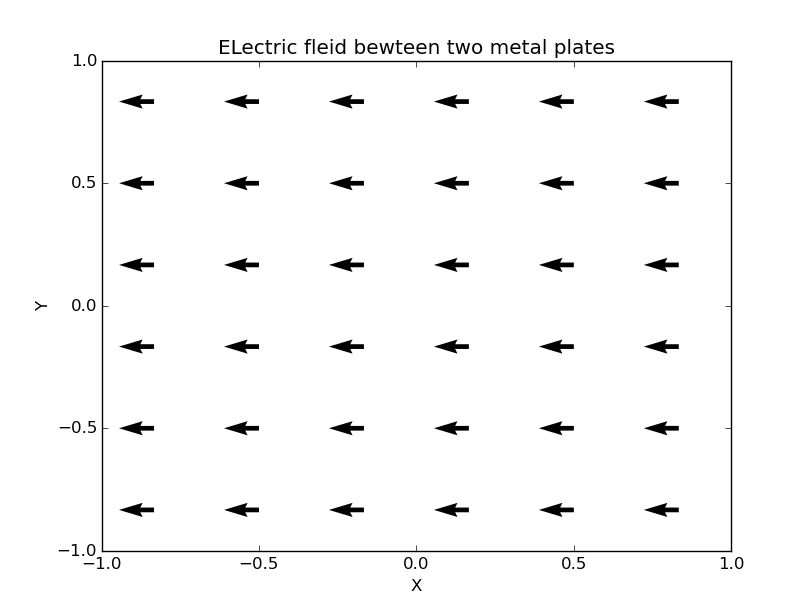
Here each arrow is oriented in the direction of $E$ at that location, and the length of each arrow is proportional to the magnitudes of the field. This is a uniform field as we expected.
Next step, we can go to a more complicated situation. Consider a capacitor in vacuum whose plates are finite, the boundary condition is obviously more complicated than the previous one. Can Jacobi method tackle this boundary condition?

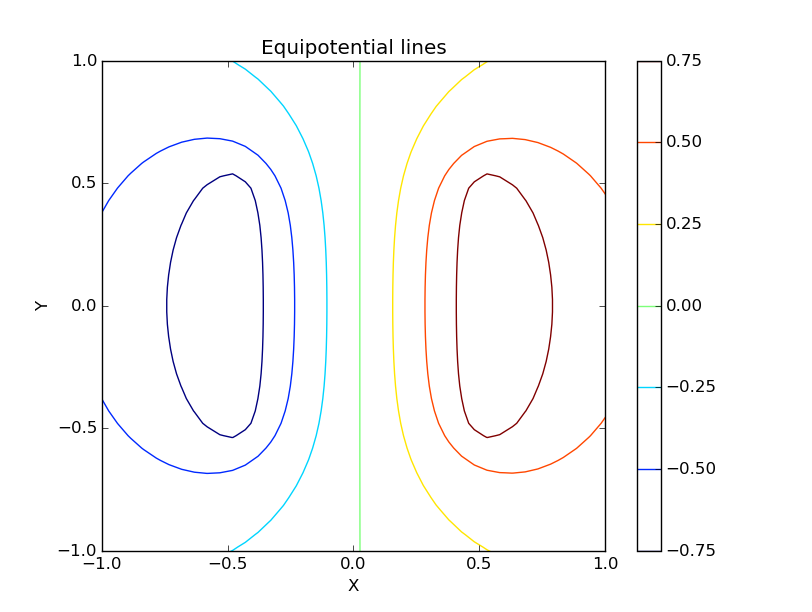
And electric field is:

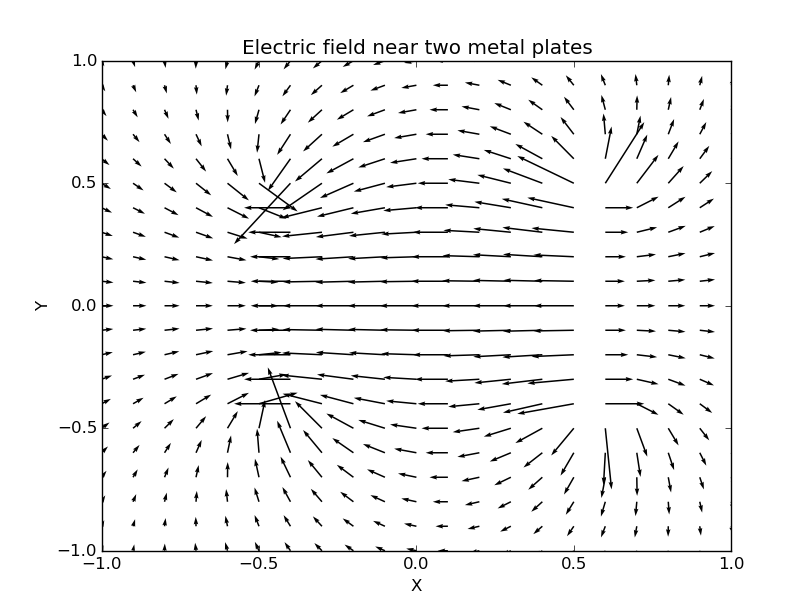
The potential and electric field full fill our expectation again, so we can confirm Jacobi method is capable of solving systems which can be described by Laplace's equation even when boundary conditions are complicated.

Conclusion

Both potential and electric field are according with our expectation. These problems show that Jacobi method is feasible for tackling problems which can be described by Laplace's equation.

program codes

potential.py

potential3.py