Chapter 2 problem 2.9

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

Use Euler method to calculate a trajectory of a baseball, air drag andthe reduced air density at high altitudes are considered. Compare results with different firing angles and determine the angle that gives the maximum range.

Introduction

The trajectory of a cannon shell is a good example of interesting physics about the mechanics of macroscopic objects which can't be solved analytically, but can be easily tackled with a computer. It involves the motion of a object through the atmosphere, so air drag must be considered, what's more, the air resistance's variation with altitude plays a key role. Let's see what's happen together!
According to some investigation, the drag force on a cannon shell can be written as

$$F_{drag}=-B_2v^2$$
where v is the speed of the shell. This force is always directed opposite to the velocity. And the density of air which treats air as an isothermal ideal gas is $$\rho=\rho_0e^{-y/y_0}$$
and we take $y_0$ as $k_BT/mg$. $g=9.8$ and $y_0\approx1.0*10^{4}$ If we treat air as an adiabatic ideal gas, which is more close to realisty, the density of air can be writeen as $$\rho=\rho_0(1-ay/T_0)^\alpha$$
where $a\approx6.5*10^{-3}K/m$, $\alpha\approx2.5$.
So we can write the ODEs as
$$\frac{d^2x}{dt^2}=-\frac{\rho B_2}{\rho_0 m}vv_x$$
$$\frac{d^2y}{dt^2}=-g-\frac{\rho B_2}{\rho_0 m}vv_y$$
Euler method can be used in this problem.

Data analysis

Air resistance

Setting the initial velocity$v_x=700 m/s$, and change the shooting angle from $35^{\circ}$ to $50^{\circ}$ and $5^{\circ}$ is the increasing step ( for we know withoutair resistance, $45^{\circ}$ is the best angle which leads to the maximum range). The results are as following:
When we do not consider air drag:

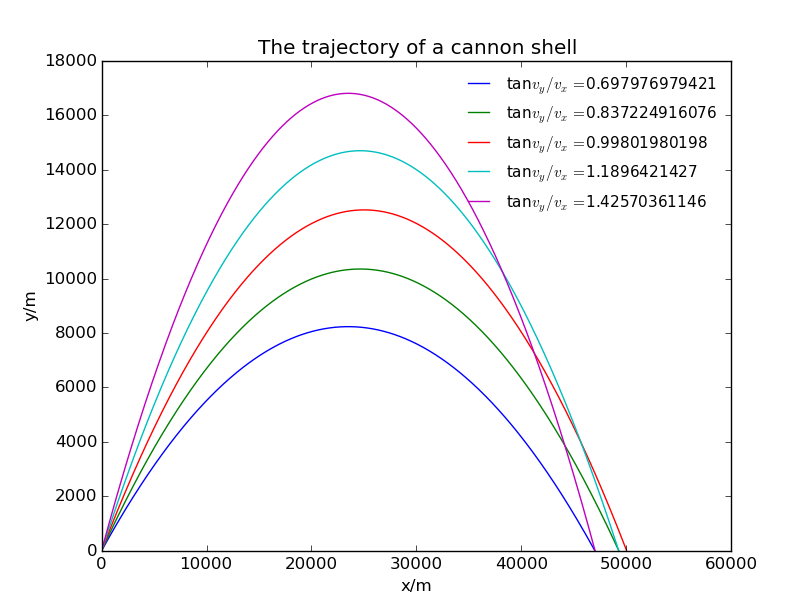
The value box in the picture refers to $v_y/v_x=tan\theta$.
$\theta=35,40,45,50,55^{\circ}$in turn. Obviously, $\theta\approx45^{\circ}$ yields to the best range.

When we try to consider air drag:

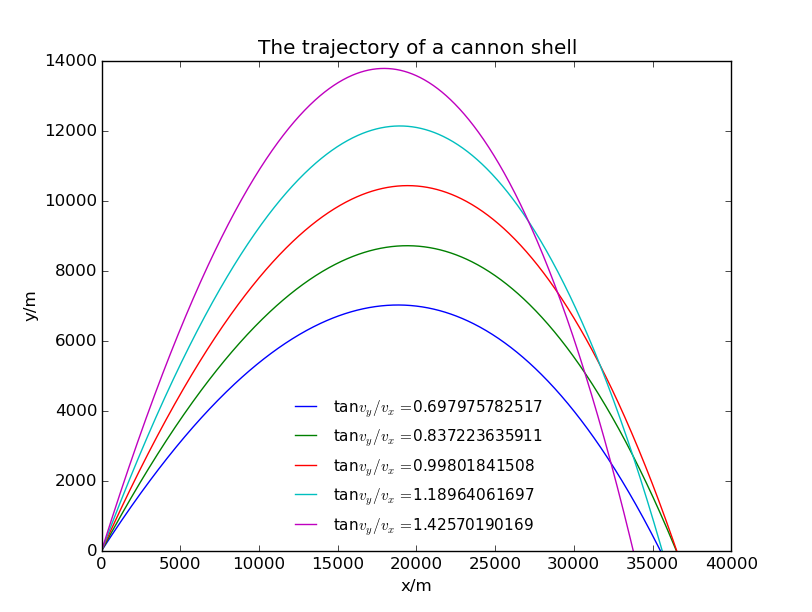
The trajectory actually change a little. And $\theta=35$ to $40^{\circ}$
yields to the maximum range.
As shown, the air resistance actually influnces the maximum range at different angles, and if you want to fix the best angle more precisely, probably we can divided 35 to 40 with 1$^{\circ}$ a step and repeat the program.

Adiabatic approximation

For the cannon shell do not travel very high, choosing adiabatic or isothermal approximation doesn't make a big difference, so we just apply the adiabatic mode of air to this problem.
When this new factor is considered and air density is changed, the result changed strikingly:

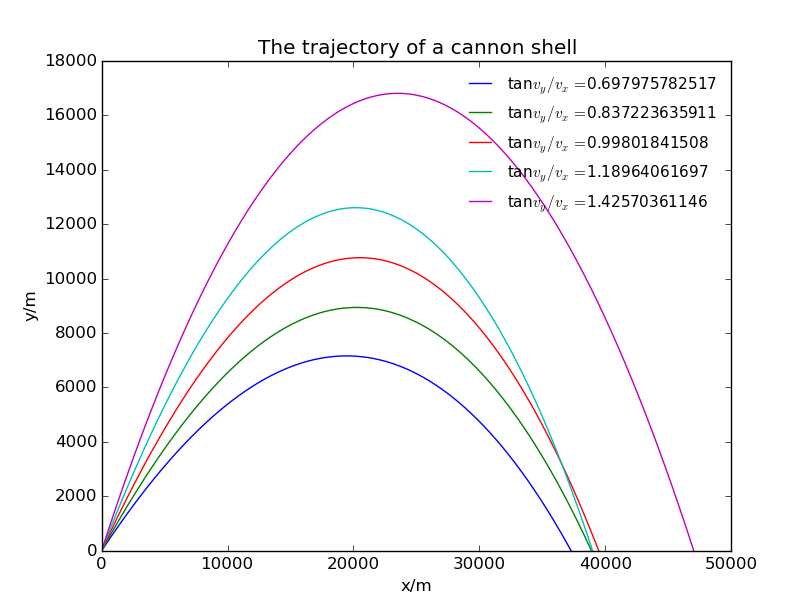
The lanuching angle $\theta=55^{\circ}$, which used to result the minimum range, now leads to the maximum range. It implys the influence of air density according to different heights actually have a key effect on the range of a cannon shell.

program codes

cannon.py