Chapter 1 problem 3.12

python.assignment

---

name: Li FangYing
number: 2013301020027

attention: you might cannot see pictures at first sight, please wait a moment

Abstract

The physical pendulum, a nonlinear, damped and driven pendulum, contains very rich and interesting phenomena. One of the most intriguing property of the physical pendulum is its chaos behavior.
In this article, driving force of rhe physical pendulum is changed to observe chaos transformation, and Lyapunov exponent will be explored as well as the phase-space plot. Finally, we come to strange attractors and investigate its properties.

Introduction

The equation of motion of the physical pendulum can be writen as follow:

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)$$ the key point is the last term, the driving force. When we include the outside force and change the driving force $F_D$, chaos behavior will raise.
Let's change it and explore a plenty of interesting phenomena!

Nummerical Approach

Again Euler cromer method is applyed.
We can rewrite the equation of motion to two first-order ODEs :

$$\frac{dw}{dt}=-g/lsin(\theta)-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)$$ $$\frac{d\theta}{dt}=w$$
However, there comes a important problem: our intuition might tell us chaotic behavior is random and unpredictable, but at the same time, we use the Euler cromer method, which is completely determined by initial values, to calculate this problem, it seems STRANGE!
In fact, the chaos behavior is deterministic and unpredictable at the same time. This is a VITAL PROPERTY for all chaos phenomena.
The unpredictable property of this system not means we cannot use Euler method, but means the system has a strong initial condition sensitiveness, which we will explore below.

Data analysis

$\theta$ versus time at different driving force

To begin the problem, let's observe the behavior of a typical physical pendulum at different driving force $F_D$.

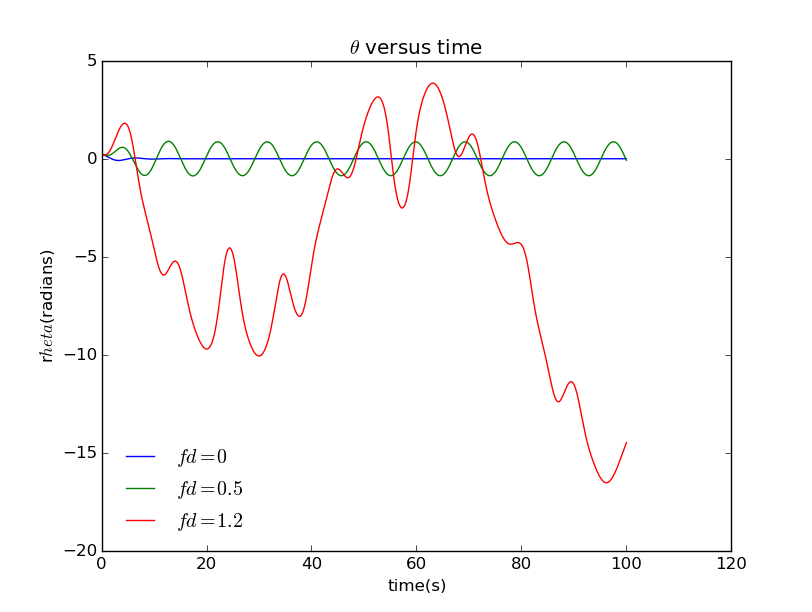
We can also limit the value range of $\theta$ in $[-\pi,\pi]$, so you can view the figure more clearly: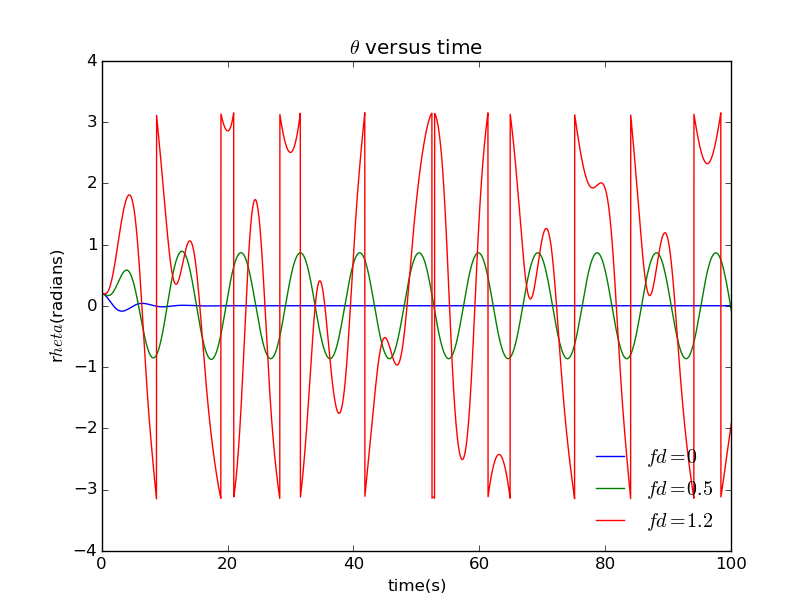
As you can see, the behavior of the physical pendulum becomes more and more random with value of $F_D$ increasing.
At low drive the motion is a simple oscillation, which could repeat forever. But when the value of $F_D$ raise, the motion of the pendulum becomes complicated and never repeat itself.
How about we fix $F_D$ and change the value of $\theta$, let's see.

the Lyapunov exponent and initial condition sensitiveness

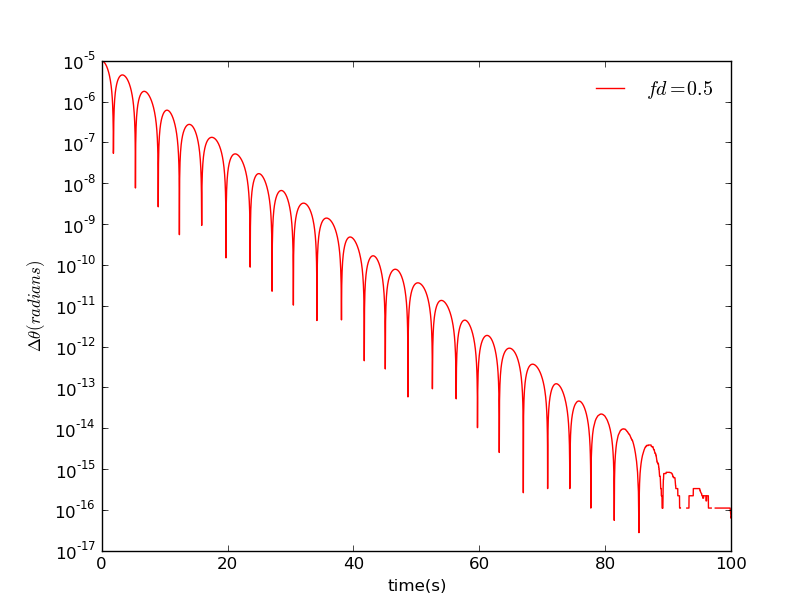
Let us consider two identical pendulums, whose only difference is we start them at SLIGHTLY different initial angles.
We set the initial angles are $2.0000$ and $2.0001$, $F_D=0.5$, and plot $\Delta\theta$ versus time :

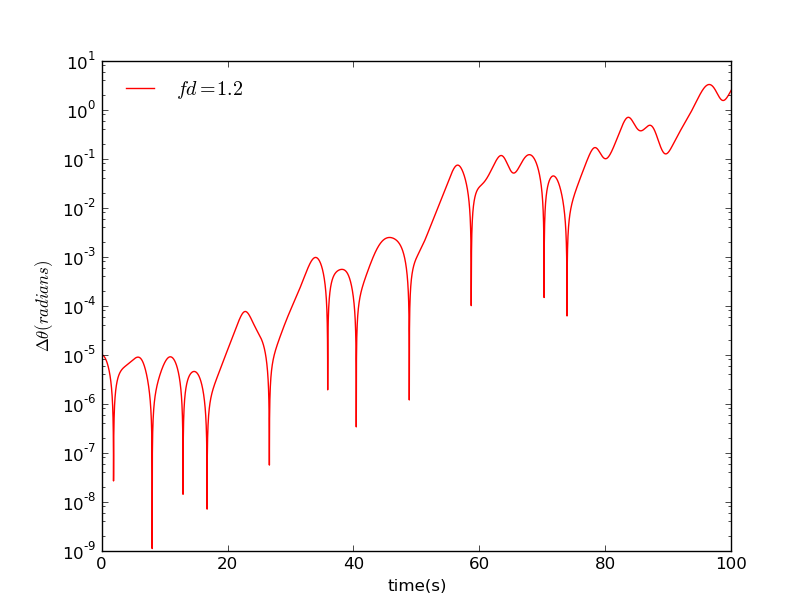
And when we raise the driving force to 1.2:

What these figures mean?
In the first figure, which the driving force is smaller, some very sharp dips occurs every 3s. These dips occur when one of the pendulum reaches a turning point. $\Delta\theta$ will vanish near the turning point since the trajectories of $\theta1$ and $\theta2$ must cross. In general, $\Delta \theta$ exhibits a steady and fairly rapid decrease with $t$.This means the motion of two pendulums becomes more and more similar.
In contrast, in the second figure, which has a larger $F_D$, you can see $\Delta \theta$ increase rapidly and irregularly with t, this trend means the system enter a somehow chaos condition.
To describe this phenomenon, we can introduce Lyapunov exponent, $\lambda$ . There is an equation:

$$\Delta \theta\approx e^{\lambda t}$$ In the former case the exponent$<0$,
which implies the system is regular, while in the later case $\lambda>0$, the transitionto chaos occurs when $\lambda=0$.

the phase-space plot

Although physical pendulum is unpredictable, it is possible to make certain accurate predictions concerning $\theta$. Let's plot the augular velocity $w$ as a function of $\theta$, which known as a phase-space plot.
With a small driving force and a larger one:

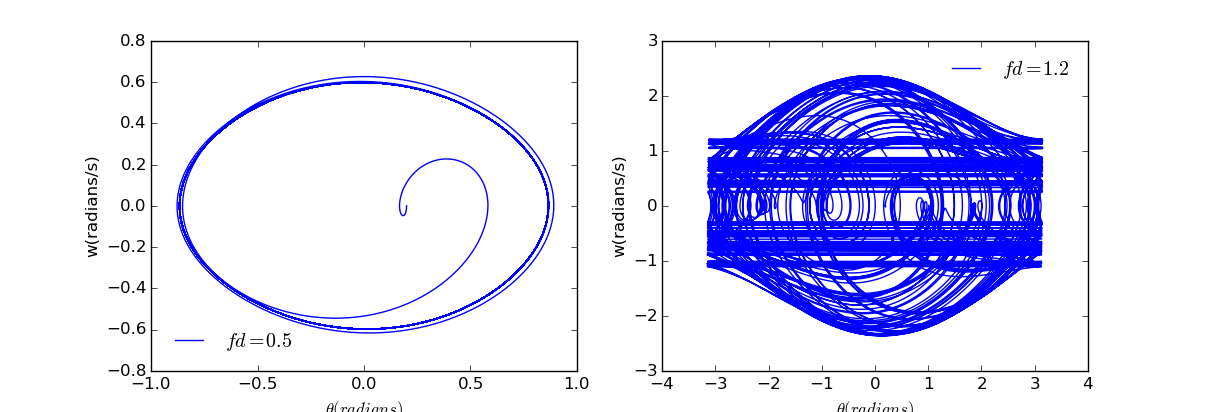
When the driving force is small, the pedulum quickly settles into a regular orbit. But when the force becomes larger, the trajectory exhibits many orbits that nearly closed and the pattern is very complicated, which is a commmon property of chaotic system.
What's more, we can only display the point when $\Omega_Dt=2n\pi$, where $n$ is an integer, which known as $\mbox{Poincare section}$. It likes a stroboscope, observing the system at set intervals. The advantage is that things looks simpler and if the system has a fixed period, the phase-space plot will just present one point:

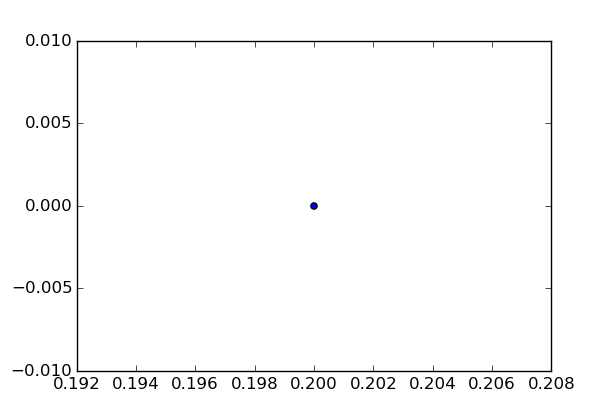
It's plotted when $F_D$=0.5, and when we raise the driving force:

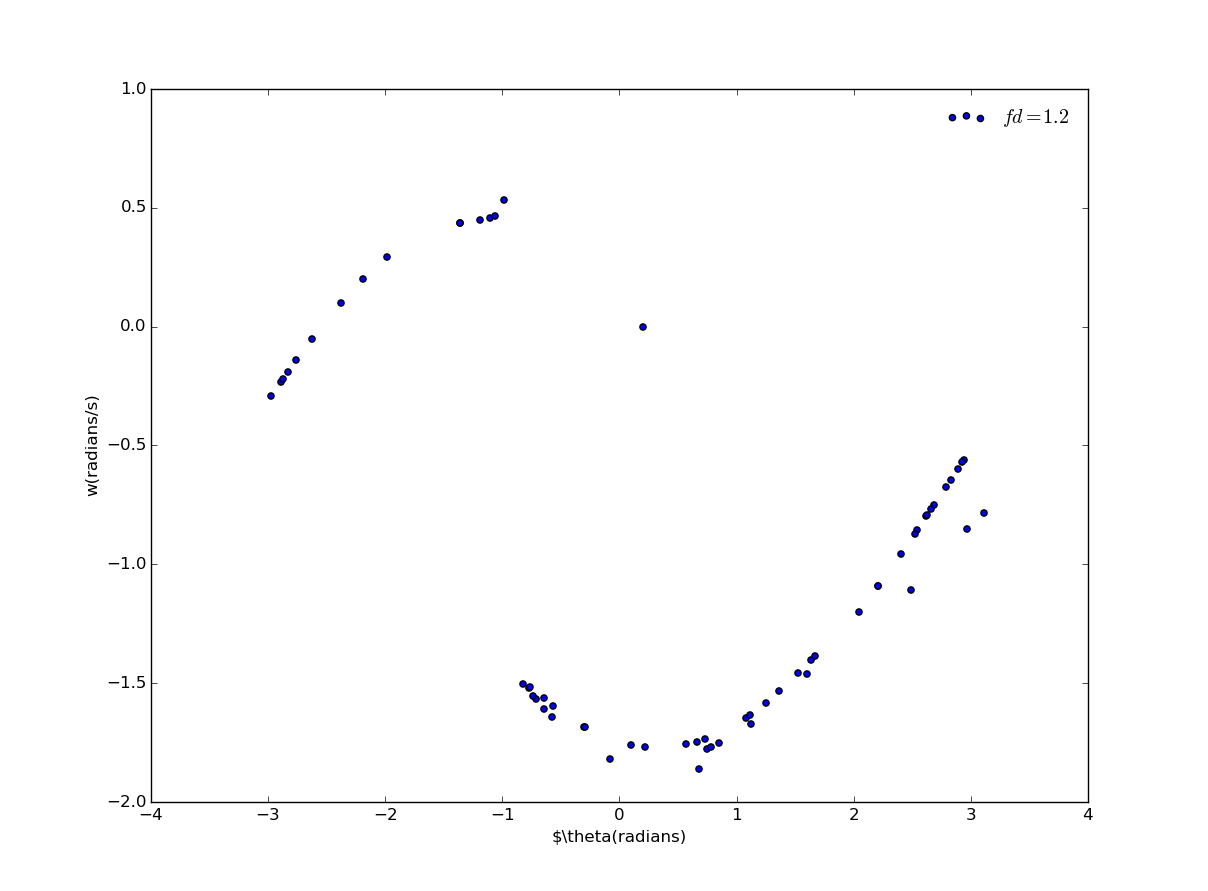
As you can see, the trajectory is very different when the system is chaotic. We can clearly tell the motion never has a period, and these points are so called attractors. While the attractors have simple forms in nonchaotic case, as the former one, they have a very complicated structure in chaotic regime, which have fractal structures and referred as strange attractors.
Change the value of $F_D,$ the results are out of prediction:


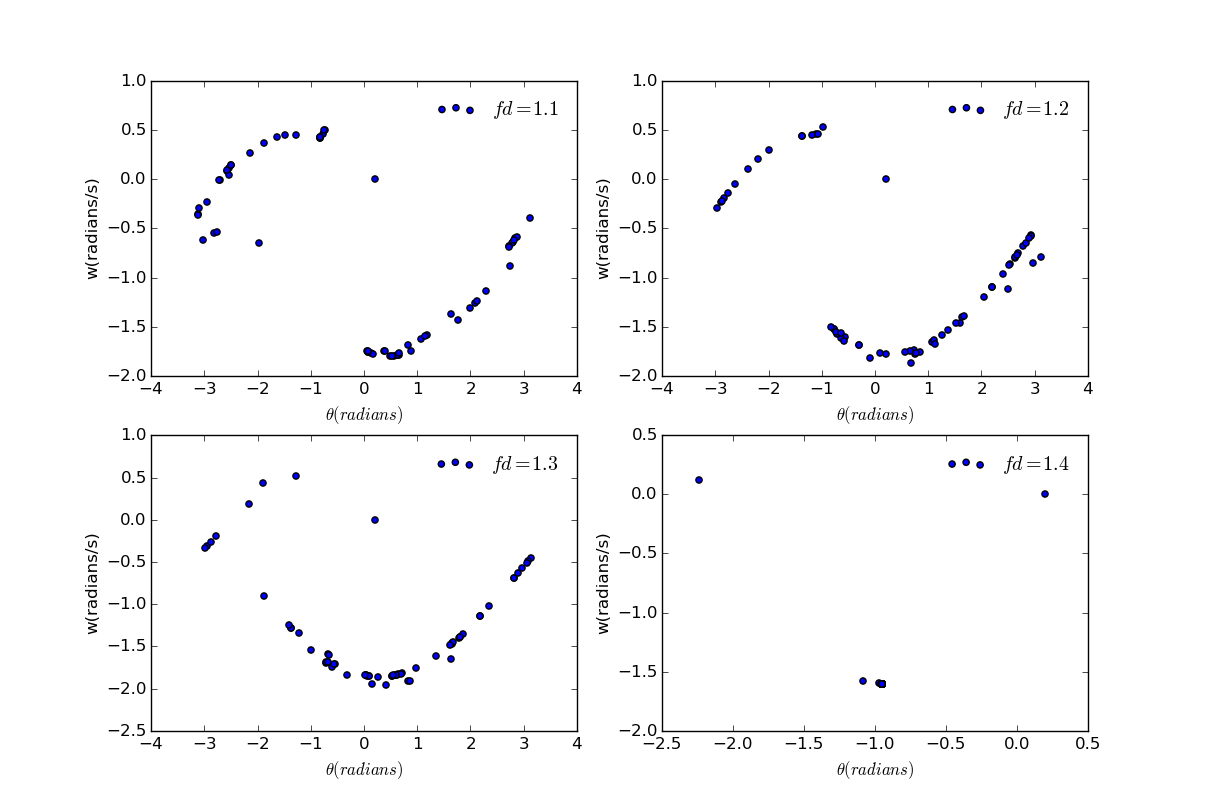
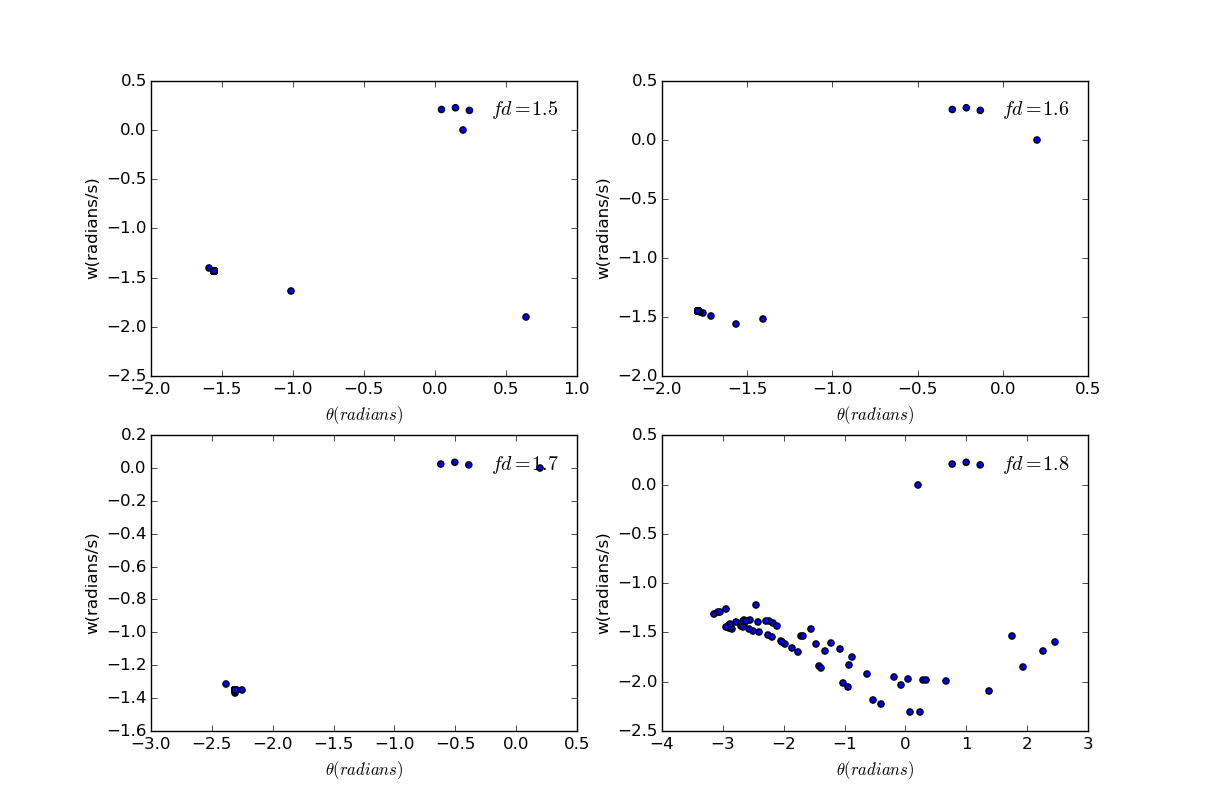
As the driving force $F_D$ increase, the trajectory doesn't become more and more random, in contrast, it becomes somewhat regular then turns to random again. In a word, the trajectory is unpredictable.
If we choose to make plot at different times, some new phenomena will emerge:
$\Omega_Dt=\pi/2,\pi,3\pi/2,2\pi:$

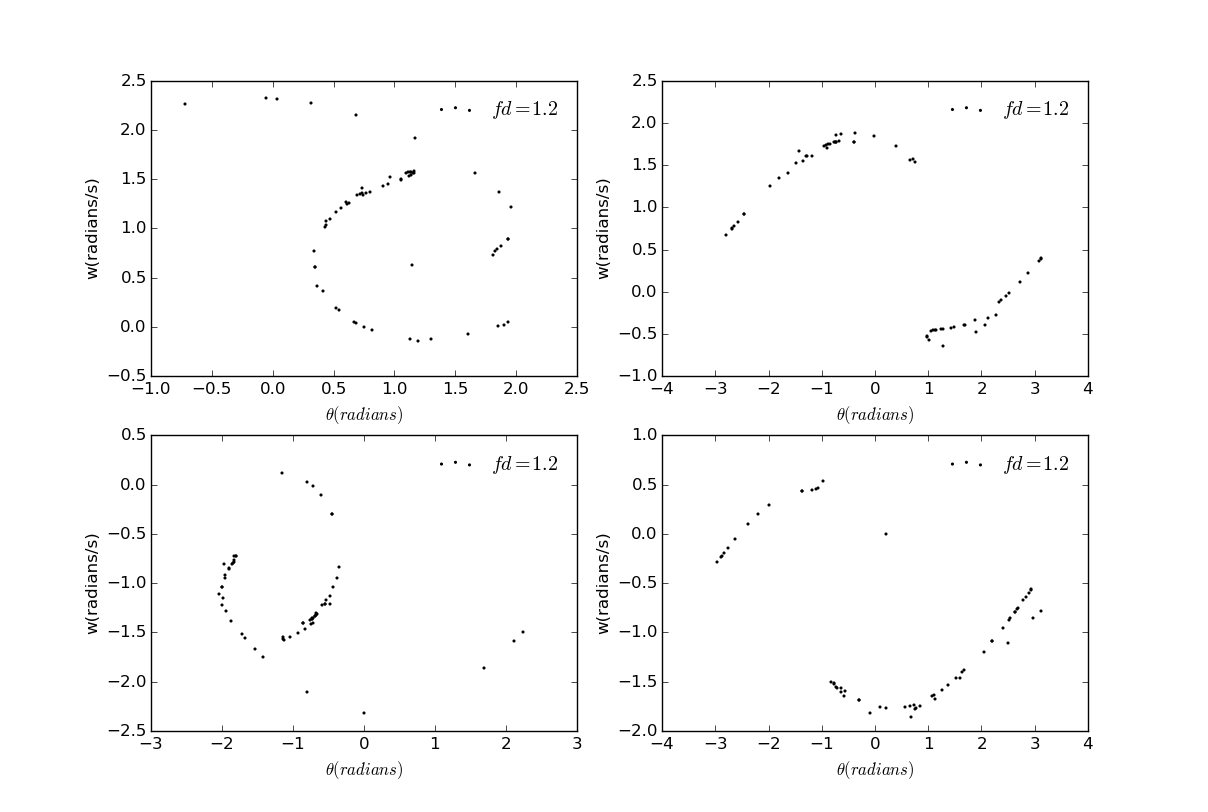
When $\Omega_Dt=\pi/2,3\pi/2$, $F_D$ reaches maximum, when $\Omega_Dt=\pi,2\pi$, the driving force cross zero. As you can see, there are some kind of symmetry in the Poincare sections at these times.

Conclusion

We explore chaotic behavior of physical pedulum and have a taste of the chaos. There are two key properties of chaos systems:

They are both deterministic and unpredictable;

The behavior of a chaos system is not completely random, it can be described by a strange attractor in phase space.

program codes

chaosp.py

THANKS

I should thank GuoShuaifei for the plotting skill he taught me.

Best wishes to you!