Chapter 4 problem 4.7

python.assignment

---

name: Li FangYing
number: 2013301020027

Abstract

Simulation of solar system in three-dimension version will be made. In addition, Two body system and binary star system will be explored and displayed in three-dimension form.

Introduction

If we want to explore fundamental physical principles such as Newton's laws, we would better find a system without friction force. The solar system is such a ideal laboratory.
Studying of the motion of celestial bodys is really inspiraing! We will begin with a sun and one planet system than go to binary star systems.

Nummerical Approach

Euler-Cromer method is a better choice than Euler method on this problem. Because the planetary motion is a oscillatory problem.
If we use Euler method, the energy of the planet will go with time, but Euler-Cromer method can exactly conserve energy over the course of each orbit. So we will take the latter one for our problem.
Consider a simple system which has a sun and a planet, the dynamic equation can be written as:

$$\frac{dv_x}{dt}=-\frac{GM_Sx}{r^3}$$ $$\frac{dx}{dt}=v_x$$ $$\frac{dv_y}{dt}=-\frac{GM_Sy}{r^3}$$ $$\frac{dy}{dt}=v_y$$
We will use astronomical units,AU and use year to measure time, and we have $GM_S=v^2r$, for simplity we take the period as 1 year, than $v=2\pi r/yr,$ so $GM_S=4\pi r^3$. For earth, $r=1(AU)$
If we consider two body problem, in which has no fixed body, there will be $8$ equations:$v_{x1},v_{x2},v_{y1},v_{y2},x_1,x_2,y_1,y_2$, and right hand of the equation will be $(x_1-x_2),(x_2-x_1),$ and so on.

Data analysis

First, we start with the simplest situation: a system with Earth and Sun:

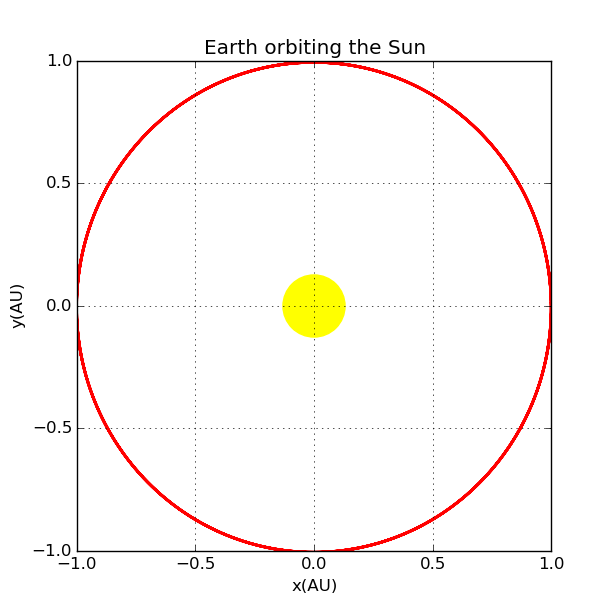
Following the fundamental principle, we can develop our own solar system. This is a 3D display of a part of the system:

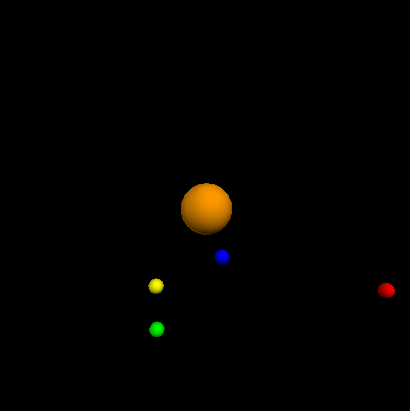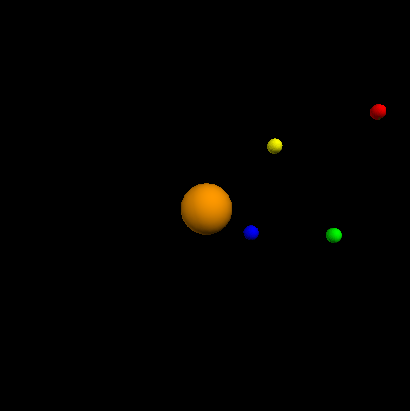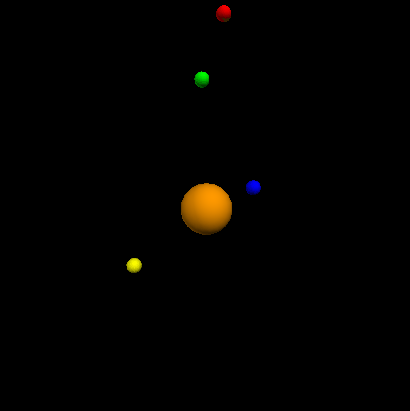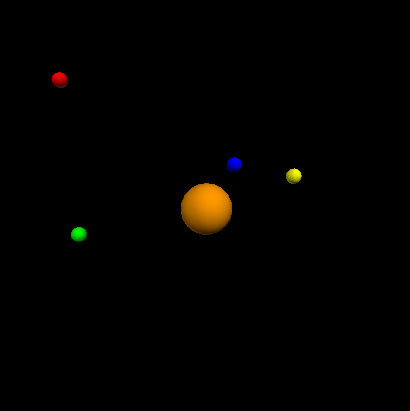
Viewing stars rotating is just a pleasures after errors and tries!

Than we let the two bodys have equal mass:
Notice that we should set the total momentum equals to zero, and the initial location is $(x1,y1)=(-1,0), (x2,y2)=(1,0)$; the initial velocity is $(vx1,vy1)=(0,-pi) (vx2,vy2)=(0,pi)$:

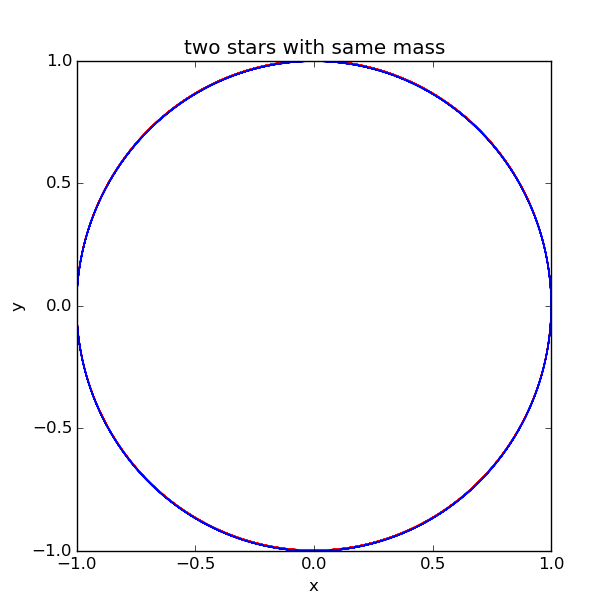
We can enlarge the figure to see it more clearly:

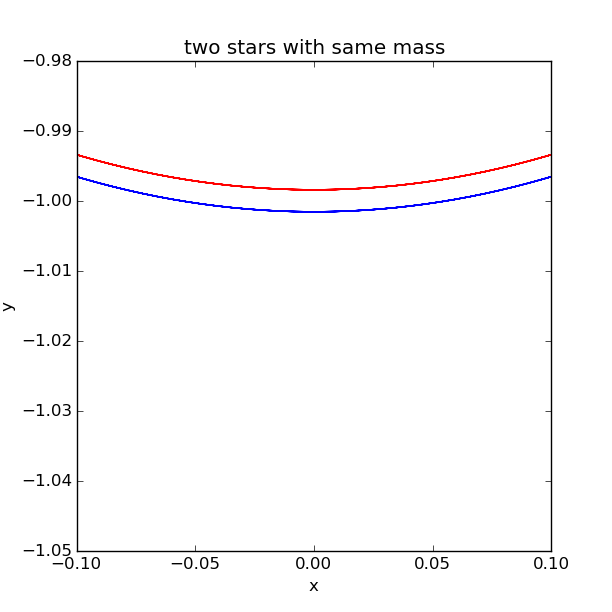
We can see the route is almost the same, but if we change the initial condition, the result will be totally differen. The result will change with initial conditions.

Next step we naturally want them have different masses, and they becomes binary stars:

The bigger one is twice as heavy as the smaller one. As you can see, the heavier one has smaller radius.

Conclusion

Today we construct our own solar system, and explore two body problem.
When two body has same masses, their trajectory is symmetric, when they have different masses, the trajectory of the heavier one has a smaller radius. If one of it is extremely heavy, the radius get down to zero and it becomes a fixed body. Besides, the trajectory will vary with the initial condition.

program codes

Earth and Sun
3D solar system
two body with equal mass
3D binary stars