stp_chap 6

姚媛媛 2014301020047

热统

---

6.1 Mean distance between particles
(a) 因为$\rho=L/N$，而粒子的平均距离为$L/N$，所以它和$\rho$的关系为$L/N=1/\rho$.
(b) 因为粒子数密度为$\rho=N/{L^2}$，平均距离$d=L/\sqrt N$, 即$d=L/\sqrt N={\rho}^{-1/2}$.
(c) 在三维情况下，同理$\rho=N/{L^3}$,粒子间的平均距离$d=L/\sqrt[3] N$, 即$d=L/\sqrt N={\rho}^{-1/3}$.

6.2 Independence of the partition function on the shape of the box
因为配分函数

$$Z_1=\sum_{n_x=1}^{\infty}\sum_{n_y=1}^{\infty}\sum_{n_z=1}^{\infty}e^{-\beta h^2[(n_x/L_x)^2+(n_y/L_y)^2+(n_z/L_z)^2]}$$
令$S_i=\sum_{n_x=1}^{\infty}e^{-\alpha_i^2n_i^2}$，其中$\alpha_i^2=\cfrac{h^2}{8mL_i^2},i=x,y,z$
根据式(6.9),类似得到： $$S_i=L_i(\cfrac{2\pi m}{\beta h^2})^{1/2}-1$$
忽略式中的$-1$项，有$S_i=L_i(\cfrac{2\pi m}{\beta h^2})^{1/2}$，
所以$Z_1=S_xS_yS_z=V(\cfrac{2\pi m}{\beta h^2})^{3/2}=\cfrac{V}{\lambda^3}$
即配分函数和盒子的形状无关。

6.3 Semiclassical limit of the single partical partition function
因为在半经典极限下，一维无限深势阱中的单粒子的配分函数可写为

$$Z_1=L(\cfrac{2\pi m}{\beta h^2})^{1/2}$$
又因为 $$\iint \cfrac{dpdx}{h}e^{-\beta p^2/2m}=\int_0^L dx\int_{-\infty}^{\infty}\cfrac{e^{-\beta p^2/2m}}{h}dp=\cfrac Lh\sqrt{\cfrac{\pi}{\beta/2m}}=L(\cfrac{2\pi m}{\beta h^2})^{1/2}.$$
所以配分函数可写为： $$Z_1=\iint \cfrac{dpdx}{h}e^{-\beta p^2/2m}$$
6.4 Equations of state of an ideal classical gas
由(6.26)式可得： $$F=-kT\ln Z_N=-kTN[\ln\cfrac VN+\cfrac 32\ln(\cfrac{2\pi mkT}{h^2})+1]$$
我们可以得到 $$P=\cfrac{1}{\beta}\cfrac{\partial \ln Z_N}{\partial V}=\cfrac{kTN}{V}$$
$$\overline E=-\cfrac{\partial}{\partial\beta}\ln Z_N=\cfrac 32N/\beta=\cfrac 32NkT$$
比较(6.15)式和(6.16)式，可知以上结果不依赖于粒子是否可分辨

Problem 6.5. Entropy of an ideal classical gas
(a) 由式(6.26)

$$F=-kT\ln Z_N=-kTN[\ln\cfrac VN+\cfrac 32\ln(\cfrac{2\pi mkT}{h^2})+1]$$
因为$S=-\partial F/\partial T$，所以可以得到 $$S(T,V,N)= Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mkT}{2\pi \hbar^2}}+\cfrac 52]$$
(b) 由6.4中的计算结果$\overline E=-\cfrac{\partial}{\partial\beta}\ln Z_N=\cfrac 32N/\beta=\cfrac 32NkT，$得到$kT=\cfrac{2\overline E}{3N}$
代入$S$的表达式中，得到 $$S(E,V,N)=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{4\pi mE}{3N h^2}}+\cfrac 52]$$
Problem 6.6. The chemical potential of an ideal classical gas
(a) $$\begin{align} \mu &= ∂F/∂N=\cfrac{∂}{∂N}\{-kTN[\ln\cfrac VN+\cfrac 32\ln(\cfrac{2\pi mkT}{h^2})+1]\}\\&=-kT\ln[\cfrac VN(\cfrac{2\pi m kT}{h^2})^{3/2}]. \end{align}$$
(b) 从(a)中的结果得到，在经典理想气体中，如果$\rho= V/N$变大，那么化学势会减少即浓度越大，化学势越低。
(c) 带入数据得 $$\begin{align} S&=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mkT}{2\pi \hbar^2}}+\cfrac 52]=-19.5186J/K. \end{align}$$
Problem 6.7. Entropy as an extensive quantity
(a) 我们已经得到的Sachur-Tetrode方程为： $$S(T,V,N)=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mkT}{2\pi \hbar^2}}+\cfrac 52]$$
所以有 $$\begin{align} S(T,\lambda V,\lambda N)&=\lambda Nk[\ln{\cfrac {\lambda V}{\lambda N}}+\cfrac 32\ln{\cfrac{mkT}{2\pi \hbar^2}}+\cfrac 52]\lambda S(T,V,N). \end{align}$$

(b)

$$Z_N=V^N(\cfrac{2\pi mkT}{h^2})^{3N/2}$$
$$F=-kT\ln Z_N=-kTN[\ln V +\cfrac 32\ln({\cfrac{2\pi mkT}{h^2}})]$$
此时熵为 $$\begin{align} S(T,V,N)=−∂F/∂T&=Nk[\ln V +\cfrac 32\ln({\cfrac{2\pi mkT}{h^2}})+\cfrac 32] \end{align}$$
此时$S$不满足 $$S(T,\lambda V,\lambda N)=\lambda S(T,V,N).$$
$S$不再是一个强度量了
(c) $g(N)$的形式应满足一个强度量的判定公式： $$g(\lambda N)=\lambda g(N)$$ 所以$g(N)$是$N$的线性函数

Problem 6.8.Etropy of mixing identical particles
(a) 由式(6.37)

$$\Delta S=k[(N_A+N_B)\ln{\cfrac{V_A+V_B}{N_A+N_B}}-N_A\ln{\cfrac{V_A}{N_A}-N_B}\ln{\cfrac{V_B}{N_B}}]$$
当$\rho=\cfrac{N_A}{V_A}=\cfrac{N_B}{V_B}$时,混合后的总浓度和混合前各自的浓度相等，即$\rho=\cfrac{V_A+V_B}{N_A+N_B}$,所以混合过程的熵变为 $$\Delta S=k[(N_A+N_B)\ln{\cfrac{1}{\rho}}-N_A\ln{\cfrac{1}{\rho}}-N_B\ln{\cfrac{1}{\rho}}]=0$$
(b)因为即使是全同粒子，在混合前两边的浓度不一样，那么混合后的浓度就与初始浓度不相同，原来粒子数浓度较大一边的部分粒子所在位置的信息丢失，所以熵变不为0

Problem 6.9. More on the entropy of mixing
(a)考虑气体A,假设它为含有N个粒子的理想气体，体积从$V$变成$2V$。熵的变化为$\Delta S=Nk\ln 2$,同理可得B气体与A相同。可以得到

$$\Delta S=2Nk\ln2$$
(b) 若系统中的粒子是可分辨的，则熵的表达式应为 $$S=Nk[\ln V +f(T,m)]$$
其中$f(T,m)=\cfrac 32\ln{\cfrac{2\pi mkT}{h^2}}+\cfrac 32.$
所以混合前各个子系统的熵为 $$S_A=N_Ak[\ln {V_A} +f(T,m_A)]\\S_B=N_Bk[\ln V_B +f(T,m_B)]$$
混合后的熵为 $$S=k[N_A\ln(V_A+V_B) +N_B\ln(V_A+V_B)+N_Af(T,m_A)+N_Bf(T,m_B)]$$
所以混合过程的熵变为 $$\Delta S=k(N_A\ln\cfrac{V_A+V_B}{V_A}+N_B\ln\cfrac{V_A+V_B}{V_B}).$$
当$N_A=N_B=N,V_A=V_B=V$时，得到 $$\Delta S=2\ln2Nk$$

Problem 6.10 Is there an upper limit to the velocity?
麦克斯韦速度分布律的表达式中，当粒子速度趋于无穷大的时候，其概率几乎等于零，即几乎不可能达到速度非常大的情况。而在统计学中，像这种小概率事件我们一般称之为不可能事件，所以不用太操心速度大于光速的情况

Problem 6.11 Simulations of the Maxwell velocity distribution
(a) 运行程序的结果如下：

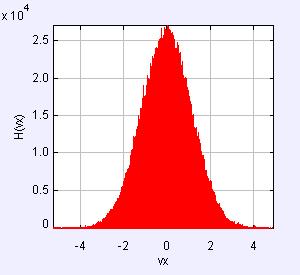
可以看到模拟的速度分布确实可以近似为麦克斯韦速度分布，温度越大，曲线的宽度越大

(b)

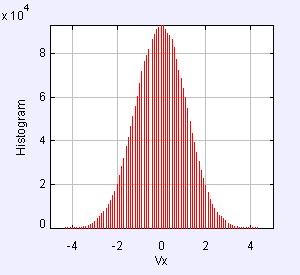
三维情况下的x方向的速度分布依然满足麦克斯韦速度分布律。根据中心极限定理，大数量的随机变量之和的值近似为一个高斯分布，所以x方向的分速度的分布是一个高斯分布

Problem 6.12. Maxwell speed distribution
(a) 麦克斯韦速度分布的取值可以为负数，是一个正态分布；而麦克斯韦速率分布的取值不能为负，所以速率分布的范围为$0\to\infty$，并且不是一个正态分布
(b) 麦克斯韦速率分布律的形式为：

$$f(v)dv=4\pi Av^2e^{-mv^2/2kT}dv,$$
由归一化条件$\int_0^{\infty}f(v)dv=1$，得到 $$\begin{align} 1&=\int_0^{\infty}4\pi Av^2e^{-mv^2/2kT}dv=4\pi A·2I(2)=A(\cfrac{2\pi kT}{m})^{3/2} \end{align}$$
其中$I_n=\int_{-\infty}^{\infty}t^xe^{-a t}dt$，为高斯积分,
当$n=2$时，$I_2=\cfrac 12(\cfrac{\pi}{a^3})^{1/2}$，所以得到 $$A=(\cfrac{m}{2\pi kT})^{3/2}$$
即麦克斯韦速率分布律为： $$f(v)dv=4\pi v^2 (\cfrac{m}{2\pi kT})^{3/2}e^{-mv^2/2kT}dv.$$
(c) $$\begin{align} \overline v&=\int_0^{\infty}4\pi v^3 (\cfrac{m}{2\pi kT})^{3/2}e^{-mv^2/2kT}dv\\&=4\pi(\cfrac{m}{2\pi kT})^{3/2}\int_0^{\infty}v^3e^{-mv^2/2kT}dv\\&=4\pi(\cfrac{m}{2\pi kT})^{3/2}\int_0^{\infty}(\cfrac{2kT}{m}t)^{3/2}e^{-t}d(\cfrac{2kT}{m}t)^{1/2}\\&=4\pi(\cfrac{m}{2\pi kT})^{3/2}·2(\cfrac{kT}{m})^2\int_0^{\infty}te^{-t}dt\\&=\sqrt{\cfrac{8kT}{\pi m}} \end{align}$$
由$\cfrac{df(v)}{dv}=0$，得到最可几速率为： $$\tilde v=\sqrt{\cfrac{2kT}{m}}$$
又有 $$\begin{align} \overline{v^2}&=\int_0^{\infty}4\pi v^4 (\cfrac{m}{2\pi kT})^{3/2}e^{-mv^2/2kT}dv\\&=4\pi(\cfrac{m}{2\pi kT})^{3/2}\int_0^{\infty}v^4e^{-mv^2/2kT}dv \end{align}$$
令$a=m/2kT$,则 $$\begin{align} \int_0^{\infty}v^4e^{-mv^2/2kT}dv&=\int_0^{\infty}v^4e^{-av^2}dv=\cfrac 12\int_{-\infty}^{\infty}v^4e^{-av^2}dv=\cfrac 12I(4)\\&=-\cfrac 12\cfrac{\partial I(2)}{\partial a}=\cfrac 38\sqrt{\pi}a^{-5/2}=\cfrac 38\sqrt{\pi}(\cfrac{m}{2kT})^{-5/2} \end{align}$$
所以 $$\overline {v^2}=4\pi(\cfrac{m}{2\pi kT})^{3/2}\cfrac 38\sqrt{\pi}(\cfrac{m}{2kT})^{-5/2}=\cfrac{3kT}m$$
所以均方根速率为： $$v_{rms}=\sqrt{\cfrac{3kT}{m}}$$
得到：$\tilde v\lt\overline v\lt v_{rms}$
(d) 令$du=dv/\sqrt{\frac{2kT}{m}}$,则 $$f(v)dv=f(u)du=4\pi{u^2}\cfrac{2kT}{m}(\cfrac{m}{2\pi kT})^{3/2}e^{-u^2}d(u\sqrt{\frac{2kT}{m}})=\cfrac{4}{\sqrt{\pi}}u^2e^{-u^2}du$$
Problem 6.13. Maxwell speed distribution in one or two dimentions
在一维情况下，速度空间仅由$v_x$构成，为一维速度空间，速率在$v,v+dv$之间的概率为$2dv·f(v)$，所以麦克斯韦速率分布为 $$F(v)=(\cfrac{2m}{\pi kT})^{1/2}e^{-mv^2/2kT}$$
在二维情况下，这时速度有$v_x,v_y$两个分量,在每个方向上均满足麦克斯韦速度分布律 $$f(v_x)=(\cfrac{m}{2\pi kT})^{1/2}e^{-mv_x^2/2kT}\\f(v_y)=(\cfrac{m}{2\pi kT})^{1/2}e^{-mv_y^2/2kT}$$
此时速度空间是$v_x,v_y$组成的二维平面，速率在$v,v+dv$之间的概率为$2\pi vdv·f(v)$，所以麦克斯韦速率分布为 $$F(v)=\cfrac{mv}{ kT}e^{-mv^2/2kT}$$
Problem 6.14.
$\overline n=0\times1/4+3\times1/4=3/4$

Problem 6.15. Mean energy of a toy model of an ideal Bose gas
(a)$\overline E=(1/6+4/6+3/6+4/6)\Delta =2\Delta$
(b)$\overline E=(2/9+6/9+4/9)\Delta =2\Delta$
(c) 对于全同的玻色子系统，其中一个粒子的平均能量为：$\overline E_1=\Delta$，
所以对于全同的玻色子满足关系式$\overline E_2=2\overline E_1$

Problem 6.16. Single particle density of states in one and two dimensions
在一维情况下，在半径小于或等于$k$内的状态数为

$$\Gamma(k)=\cfrac{Lk}{\pi}$$ 所以得到$k$和$k+dk$内的状态数为 $$g(k)dk=\cfrac{d\Gamma(k)}{dk}dk=\cfrac{L}{\pi}dk$$
二维情况下，k空间由$n_x,n_y$构成，即$\overrightarrow k=(n_x,n_y)\cfrac{\pi}{L}$,在半径小于或等于$k$内的状态数为 $$\Gamma(k)=\cfrac 14\pi(\cfrac{Lk}{\pi})^2$$
所以得到$k$和$k+dk$内的状态数为 $$g(k)dk=\cfrac{d\Gamma(k)}{dk}dk=\cfrac{L^2k}{2\pi}dk$$
Problem 4.17. Density of states in one and two dimensions
在一维情况下$\Gamma(k)=\cfrac{Lk}{\pi}$，则$\Gamma(\epsilon)=\cfrac{L}{\pi}(\cfrac{2m\epsilon}{\hbar^2})^{1/2}$，所以有
$$g(\epsilon)=\cfrac{d\Gamma(\epsilon)}{d\epsilon}=\cfrac{L}{\pi\hbar}(\cfrac{m}{2\epsilon})^{1/2}$$
在二维情况下，在k空间中在半径小于或等于k内的状态数为： $$\Gamma(k)=\cfrac 14\pi(\cfrac{Lk}{\pi})^2$$
由式（6.102）和（6.103）有 $$\epsilon=\cfrac{\hbar^2k^2}{2m}，d\epsilon=\cfrac{\hbar^2k}{m}dk$$ 所以 $$k=(\cfrac{2m\epsilon}{\hbar^2})^{1/2}，\Gamma(\epsilon)=\cfrac 14\pi(\cfrac{L}{\pi})^2 \cfrac{2m\epsilon}{\hbar^2}=\cfrac{mL^2}{2\pi\hbar^2}\epsilon$$
进而得到： $$g(\epsilon)=\cfrac{d\Gamma(\epsilon)}{d\epsilon}=\cfrac{mL^2}{2\pi\hbar^2}$$
Problem 6.18. Relativistic particles
对于相对论性粒子有 $$\epsilon^2=p^2c^2+m^2c^4=\hbar^2k^2c^2+m^2c^4$$ 所以 $$k=(\cfrac{\epsilon^2-m^2c^4}{\hbar^2c^2})^{1/2}\\dk=\cfrac{1}{\hbar c}(\cfrac{\epsilon^2}{\epsilon^2-m^2c^4})^{1/2}d\epsilon$$
得到 $$\Gamma(\epsilon)=\cfrac 18\cfrac{4\pi}{3}(\cfrac{L}{\pi})^3(\cfrac{\epsilon^2-m^2c^4}{\hbar^2c^2})^{3/2}$$
得到态浓度为： $$\begin{align} g(\epsilon)&=\cfrac{d\Gamma(\epsilon)}{d\epsilon}=\cfrac{L^3\epsilon}{2\pi^2\hbar c}(\epsilon^2-m^2c^4)^{1/2}. \end{align}$$
Problem 6.19. Relation between the energy and pressure equations of state for a nonrelativistic ideal gas
$$E=\int_0^{\infty}\epsilon\overline n(\epsilon)g(\epsilon)d\epsilon=n_s\cfrac{V}{4\pi^2\hbar^3}(2m)^{3/2}\int_0^{\infty}\cfrac{\epsilon^{3/2}d\epsilon}{e^{\beta(\epsilon-\mu)}±1}$$

$$\Omega=∓kT\int_0^{\infty}g(\epsilon)\ln[1±e^{-\beta(\epsilon-\mu)}]=∓kT\cfrac{n_sV}{4\pi^2\hbar^3}(2m)^{3/2}\int_0^{\infty}\epsilon^{1/2}\ln[1±e^{-\beta(\epsilon-\mu)}]d\epsilon$$

作分部积分，得到：

$$\Omega=-\cfrac 23n_s\cfrac{V}{4\pi^2\hbar^3}(2m)^{3/2}\int_0^{\infty}\cfrac{\epsilon^{3/2}d\epsilon}{e^{\beta(\epsilon-\mu)}±1}$$

即$\Omega=-\cfrac 23E$，又$\Omega=-PV$,所以有

$$PV=\cfrac 23 E$$

Problem 6.20. Relation between the energy and pressure equations of state for photons

$$E=\int_0^{\infty}\epsilon\overline n(\epsilon)g(\epsilon)d\epsilon=\cfrac{V}{\pi^2\hbar^3c^3}\int_0^{\infty}\cfrac{\epsilon^3d\epsilon}{e^{\beta(\epsilon-\mu)}+1}$$

$$\Omega=-kT\int_0^{\infty}g(\epsilon)\ln[1+e^{-\beta(\epsilon-\mu)}]=-kT\cfrac{V}{\pi^2\hbar^3c^3}\int_0^{\infty}\epsilon^2ln[1+e^{-\beta(\epsilon-\mu)}]d\epsilon$$
作分部积分得： $$\Omega=-\cfrac 13\cfrac{V}{\pi^2\hbar^3c^3}\int_0^{\infty}\cfrac{\epsilon^3d\epsilon}{e^{\beta(\epsilon-\mu)}+1}$$
又$\Omega=-PV$,所以得到 $$PV=\cfrac 13E$$
Problem 6.21. The chemical potential
(a) 标准条件下1摩尔单原子理想气体的$T=273.15K,N=6.02\times10^{23},V=0.0224m^3$,假设原子质量为$m=1.672\times10^{-27}kg$,所以其化学势为： $$\mu=kT\ln[\cfrac{N}{V}(\cfrac{2\pi \hbar^2}{mkT})^{3/2}]=-3.908\times10^{-20}J.$$

(b) 已知

$$\overline N=V(\cfrac{m}{2\pi\hbar^2\beta})^{3/2}e^{\beta\mu}$$

因为热德布罗意波长为$\lambda=(\cfrac{h^2}{2\pi mkT})^{1/2}=(\cfrac{m}{2\pi\hbar^2\beta})^{-1/2}$,所以

$$\overline N=\cfrac{V}{\lambda^3}e^{\beta\mu}$$

又记$\rho=\overline N/V,$所以得到化学势表达式为：

$$\mu(T,V)=-kT\ln\cfrac 1{\rho\lambda^3}.\tag{6.117}$$
(c) 由(6.87)式和$\overline n_k<<1$： $$\overline n_k=e^{-\beta(\epsilon_k-\mu)}\tag{6.87}，\overline n_k<<1$$
由于$\epsilon_k$可以任意，所以$\mu\to-\infty$，又由(6.117)可得：${\rho\lambda^3}<<1$，即 $$\lambda<<\rho^{-1/3}$$
Problem 6.22. Ideal gas equations of state
$$P=\cfrac{kT}{\lambda^3}e^{\beta\mu}，\overline N=\cfrac{V}{\lambda^3}e^{\beta\mu}$$
将两式作比消去$\mu$得到：$\cfrac{P}{N}=\cfrac{kT}{V}$,
即 $$PV=NkT$$
再利用在前面得到的关系式$PV=\cfrac 23E$,得到： $$E=-kTN+\cfrac52kNT=\cfrac32kNT$$
Problem 6.23. Wien's displacement law
方程 $$(3-x)e^x=3$$ 的数值解,除$x=0$之外的另一个根为$x=2.822$

Problem 6.24. Derivation of the Rayleigh-Jeans and Wien's laws
(a)

$$u(\nu)d\nu=\cfrac{8\pi h\nu^3}{c^3}\cfrac{d\nu}{e^{\beta h\nu}-1}$$

利用波长和频率的关系$\lambda=c/\nu$,作变量代换，得到

$$\begin{align} u(\lambda)d(-\lambda&)=\cfrac{8\pi h(c/\lambda)^3}{c^3}\cfrac{-c/\lambda^2d\lambda}{e^{\beta hc/\lambda}-1}=-\cfrac{8\pi hc}{\lambda^5}\cfrac{d\lambda}{e^{\beta hc/\lambda}-1} \end{align}$$ 所以： $$u(\lambda)=\cfrac{8\pi hc}{\lambda^5}\cfrac{1}{e^{\beta hc/\lambda}-1}.$$
(b) 当$\lambda\to\infty$时，有$e^{\beta hc/\lambda}-1\sim\beta hc/\lambda$，所以有 $$\begin{align} u(\lambda)d\lambda&=\cfrac{8\pi hc}{\lambda^5}\cfrac{d\lambda}{e^{\beta hc/\lambda}-1}=\cfrac{8\pi hc}{\lambda^5}\cfrac{d\lambda}{\beta hc/\lambda}=\cfrac{8\pi kT}{\lambda^4}d\lambda \end{align}$$
(c) 当$\lambda\to0$时，$u(\lambda)\to \infty$
(d) 当$\lambda\to0$时， $e^{\beta hc/\lambda}>>1$,所以我们忽略掉减1的这一项，得到维恩公式： $$u(\lambda)=\cfrac{8\pi hc}{\lambda^5}{e^{-\beta hc/\lambda}}d\lambda.$$
Problem 6.25. Thermodynamics of blackbody radiation
(1) $$u(\nu)=\cfrac{8\pi h\nu^3}{c^3}\cfrac{1}{e^{\beta h\nu}-1}$$ $$\begin{align} E&=V\int_0^{\infty}u(\nu)d\nu=V\cfrac{8\pi h}{c^3}\int_0^{\infty}\cfrac{(kT/h)^4 x^3}{e^x-1}dx=V\cfrac{8\pi k^4T^4}{h^3c^3}\cfrac{\pi^4}{15}=\cfrac{4\sigma}{c}VT^4. \end{align}$$
其中，$\int_0^{\infty}\cfrac{ x^3}{e^x-1}dx=\cfrac{\pi^4}{15},\sigma=\cfrac{2\pi^5k^4}{15h^3c^2}$.
(2) 在problem6.20中已经求得，对于光子有$PV=\cfrac 13E，$所以朗道势为： $$\Omega=-PV=-\cfrac 13E=-\cfrac{4\sigma}{3c}VT^4$$
且因为在我们的模型中化学势消失，所以正则系综和巨正则系综的配分函数相同，所以有$F=\Omega$.
(3) 由热力学关系式$S=-\cfrac{\partial\Omega}{\partial T}$,得到 $$S=-\cfrac{\partial\Omega}{\partial T}=\cfrac{16\sigma}{3c}VT^3.$$
(4) 由热力学关系式$P=-\cfrac{\partial\Omega}{\partial V}$,得到 $$P=-\cfrac{\partial\Omega}{\partial V}=\cfrac{4\sigma}{3c}T^4=\cfrac 13\cfrac EV.$$
(5) 由(2)中的推导可知 $$G=F+PV=0.$$

Problem 6.26. Mean number of photons

$$\begin{align} N&=\int_0^{\infty}\overline n(\epsilon)g(\epsilon)d\epsilon=\cfrac{V}{\pi^2\hbar^3c^3}\int_0^{\infty}\cfrac{\epsilon^2d\epsilon}{e^{\beta\epsilon}-1}=\cfrac{V}{\pi^2\hbar^3c^3}\int_0^{\infty}\cfrac{(\hbar w)^2d(\hbar w)}{e^{\hbar w/kT}-1}=\cfrac{V(kT)^3}{\pi^2\hbar^3c^3}\int_0^{\infty}\cfrac{x^2dx}{e^x-1}\\&=2\times1.202\cfrac{V(kT)^3}{\pi^2\hbar^3c^3}=0.244V(\cfrac{kT}{\hbar c})^3. \end{align}$$

Problem 6.27. Order of magnitude estimates
(a) 因为$1eV=1.602\times10^{-19}J,k=1.381\times1^{-23}J/K$,所以由已知的费米能，可以计算得到费米温度:

$$T_F(Li)=\cfrac{\epsilon_F(Li)}{k}=\cfrac{4.7\times1.602\times10^{-19}J}{1.381\times1^{-23}J/K}=5.5\times10^4K\\T_F(Na)=\cfrac{\epsilon_F(Na)}{k}=\cfrac{3.2\times1.602\times10^{-19}J}{1.381\times1^{-23}J/K}=3.7\times10^4K\\T_F(Al)=\cfrac{\epsilon_F(Al)}{k}=\cfrac{11.7\times1.602\times10^{-19}J}{1.381\times1^{-23}J/K}=13.6\times10^4K\\T_F(Cu)=\cfrac{\epsilon_F(Cu)}{k}=\cfrac{7\times1.602\times10^{-19}J}{1.381\times1^{-23}J/K}=8.1\times10^4K\\T_F(Ag)=\cfrac{\epsilon_F(Ag)}{k}=\cfrac{5.5\times1.602\times10^{-19}J}{1.381\times1^{-23}J/K}=6.4\times10^4K$$
(b) 室温一般可取为：300K,可见，和室温相比，(a)中计算出的各金属的费米温度都很高。对于室温，有$kT=1.381\times10^{-23}\times300=4.143\times10^{-21}J=0.02586 eV$
(c) 由 $$\epsilon_F=\cfrac{\hbar^2}{2m}(3\pi^2\rho)^{2/3}，\rho=\cfrac{1}{3\pi^2}(\cfrac{2m\epsilon_F}{\hbar^2})^{3/2}$$ 对于Li和Cu,分别代入它们的费米能量，并代入电子质量$m=9.1\times10^{-31}kg$,可以求得它们的电子浓度分别为： $$\rho_{Li}=4.7\times10^{28}m^{-3}\\\rho_{Cu}=8.5\times10^{28}m^{-3}$$
(d) 粒子间的平均距离为粒子数浓度的三次方根的倒数，我们用d表示，所以$d=\rho^{-1/3}$
$$d_{Li}=\rho_{Li}^{-1/3}=0.277nm\\d_{Cu}=\rho_{Cu}^{-1/3}=0.227nm$$
(e) 假设温度为Li的费米温度，则此时电子的德布罗意波长为 $$\begin{align} \lambda&=(\cfrac{h^2}{2\pi m kT})^{1/2}\\&=0.9989nm \end{align}$$
(f) 可以看到在费米温度下电子的德布罗意波长大于电子的平均距离。

Problem 6.28. Landau potential at zero temperature

$$\Omega=-kT\int_0^{\infty}g(\epsilon)\ln[1+e^{-\beta(\epsilon-\mu)}]d\epsilon$$ 对于$T\to0$,则在能量小于化学势部分得到$\ln[1+e^{-\beta(\epsilon-\mu)}]\to\ln e^{-\beta(\epsilon-\mu)}=-\beta(\epsilon-\mu)$,而在能量大于化学势那部分没有电子占据，所以 $$\begin{align} \Omega&=\cfrac{V(2m)^{3/2}}{2\pi^2\hbar^3}\int_0^{\epsilon_F}\epsilon^{1/2}(\epsilon-\epsilon_F)d\epsilon=-\cfrac{4\epsilon^{5/2}}{15}\cfrac{V(2m)^{3/2}}{2\pi^2\hbar^3}=-\cfrac{2V(2m)^{3/2}\epsilon^{5/2}}{15\pi^2\hbar^3} \end{align}$$
所以在T=0时的压强为 $$P=-\cfrac{\partial\Omega}{\partial V}=\cfrac{2(2m)^{3/2}\epsilon^{5/2}}{15\pi^2\hbar^3}$$

Problem 6.29. Show that the limit (6.145) for $\overline n(\epsilon)$ at T = 0 follows only if µ > 0
因为

$$\overline n(\epsilon)=\cfrac{1}{e^{\beta(\epsilon-\mu)}+1}$$
当$\mu>0$时，令$T\to0$,即$\beta\to\infty$,所以得到 $$\overline n(\epsilon)=\begin{cases}1,\epsilon<\mu\\0,\epsilon>\mu\end{cases}\tag{6.145}$$
当$\mu\lt0$时，$T\to0$,即$\beta\to\infty$,会导致$e^{\beta(\epsilon-\mu)}\to\infty$,结果使$\overline n(\epsilon)\to0.$
当$\mu=0$时，$\epsilon$也只能是0，所以$\overline n(\epsilon)=1$.
所以，只有当$\mu>0$时，才满足式（6.145）

Problem 6.30. Numerical evaluation of the chemical potential for an ideal Fermi gas
(a) $T^{*}=0.2$时，$\mu^*=0.967$
$T^{*}=0.3$时，$\mu^*=0.936$
$T^{*}=0.4$时，$\mu^*=0.843$
可见，开始时随着温度升高，化学势降低；
$T^{*}=10$时，$\mu^*=-37.28$
$T^{*}=100$时，$\mu^*=-633.8$
所以当$T^*>>1$时，$-\mu>>1$.
(b) $T^*=0.99$时，$\mu^*\approx0$.
(c) E(T)是关于T的线性增函数，$C_V(T)$是T的线性增函数。

Problem 6.31. Low temperature behavior
(a) 由

$$g(\epsilon)d\epsilon=\cfrac{V(2m)^{3/2}}{2\pi^2\hbar^3}\epsilon^{1/2}d\epsilon\tag{6.105}$$
当$\epsilon=\epsilon_F$时， $$\begin{align} g(\epsilon_F)&=\cfrac{V(2m)^{3/2}}{2\pi^2\hbar^3}\epsilon_F^{1/2}=\cfrac{V}{2\pi^2}(\cfrac{2m}{\hbar^2})^{3/2}\epsilon_F^{1/2}\\&=\cfrac{V}{2\pi^2}(\cfrac{2m}{\hbar^2(3\pi^2\rho)^{2/3}})^{3/2}·3\pi^2\rho\epsilon_F^{1/2}=\cfrac{V}{2}\cfrac{3\rho}{\epsilon_F^{3/2}}\epsilon_F^{1/2}=\cfrac{3N}{2\epsilon_F}=\cfrac{3N}{2kT_F}. \end{align}$$
(b) 因为 $$\rho=\cfrac{(2m)^{3/2}}{3\pi^2\hbar^3}\mu^{3/2}\left[1+\cfrac{\pi^2}{8}(kT)^2\mu^{-2}\right]$$
所以
$$\begin{align} P&=-\cfrac{\partial\Omega}{\partial V}=\cfrac{(2m)^{3/2}}{3\pi^2\hbar^3}\left[\cfrac 25\mu^{5/2}+\cfrac{\pi^2}{4}(kT)^2\mu^{1/2}\right]=\cfrac 25\rho\epsilon_F\left[1+\cfrac {5\pi^2}{12}(\cfrac{T}{T_F})^2+···\right] \end{align}$$
(c) 由$PV=\cfrac 23E$，得到 $$\begin{align} E&=\cfrac 32PV=\cfrac 32V\cfrac 25\rho\epsilon_F\left[1+\cfrac {5\pi^2}{12}(\cfrac{T}{T_F})^2+···\right]\\&=\cfrac 35V\rho\epsilon_F\left[1+\cfrac {5\pi^2}{12}(\cfrac{T}{T_F})^2+···\right] \end{align}$$
(d) $$\begin{align} S&=-\cfrac{\partial\Omega}{\partial T}=\cfrac{V(2m)^{3/2}}{3\pi^2\hbar^3}·\cfrac {\pi^2}2k^2T\mu^{1/2}=\cfrac{\rho V}{\epsilon_F}·\cfrac {\pi^2}2k^2\epsilon^{1/2}=\cfrac {\pi^2}2k^2N\cfrac{T}{kT_F}=\cfrac {\pi^2}2kN\cfrac{T}{T_F}. \end{align}$$

Problem 6.32. Effective electron mass
由式(6.174)

$$C_V=\cfrac {\pi^2}2kN\cfrac{T}{T_F}\tag{6.174}$$ 得到 $$C_V/NkT=\cfrac{\pi^2}{2T_F}$$
对于铜有$T_F=8.2\times10^{4}K$,所以 $$C_V/NkT=\cfrac{\pi^2}{2\times8.2\times10^{4}K}=6.02\times10^{-5}K^{-1}$$
这和实验得到的值$8\times10^{-5}K^{-1}$有差别，将电子质量修正为有效质量$m^*=1.3m_e$,得到 $$C_V/NkT=1.3\times\cfrac{\pi^2}{2\times8.2\times10^{4}K}=7.8\times10^{-5}K^{-1}$$
这个等效质量和铜原子核的质量有关。

Problem 6.33. Temperature dependence of the chemical potential in two dimensions
(a) 在二维情况下单粒子微观态浓度为$g(\epsilon)=\cfrac{mA}{2\pi\hbar^2}$，对于电子，还应考虑其自旋，所以电子的单粒子态浓度为

$$g(\epsilon)=\cfrac{mA}{\pi\hbar^2}$$
所以总电子数的平均值为 $$\begin{align} \overline N&=\int_0^{\infty}\overline n(\epsilon)g(\epsilon)d\epsilon=\cfrac{mA}{\pi\hbar^2}\int_0^{\infty}\cfrac{1}{e^{\beta(\epsilon-\mu)}+1}\\&=\cfrac{mA}{\pi\hbar^2}kT\ln\cfrac{e^{\beta\epsilon}}{e^{\beta(\epsilon-\mu)}+1}|_0^{\infty}=\cfrac{mA}{\pi\hbar^2}kT\ln(1+e^{\beta\mu}) \end{align}$$
其中$\rho=\overline N/A$.
所以得到 $$\mu(T)=kT\ln(e^{\rho\pi\hbar^2/mkT}-1).$$
(b) 当T=0时，总平均粒子数为： $$\begin{align} \overline N&=\int_0^{\epsilon_F}g(\epsilon)d\epsilon=\cfrac{mA}{\pi\hbar^2}\epsilon_F \end{align}$$
所以得到：
$$\epsilon_F=\mu(T=0)=\rho\pi\hbar^2/m.$$
当$T>>T_F$时，$e^{\rho\pi\hbar^2/mkT}-1\approx\rho\pi\hbar^2/mkT$,所以 $$\mu=kT\ln\cfrac{\rho\pi\hbar^2}{mkT}.$$

Problem 6.34. Limiting behavior of the heat capacity in the Einstein model
已知

$$C_V=3Nk(\cfrac{T_E}{T})^2\cfrac{e^{T_E/T}}{e^{T_E/T}-1}$$
令$x=T_E/T$,当$T>>T_E$即$x\to0$时，$e^x\approx1+x$,所以 $$x^2e^x/(e^x-1)^2\approx1+x$$ ,我们假设x进一步趋于0，则有$1+x\approx1$,得到 $$C_V=3Nk$$
当$T<<T_E$即$x\to\infty$时，$e^x>>1$,所以$e^x-1\approx e^x$，所以 $$C_V=3Nkx^2e^{-x}=3Nk(\cfrac{\hbar w}{kT})^2e^{-\hbar w/kT}.$$

Problem 6.35. More on the Einstein and Debye theories
(a)

$$\lambda_D=2\pi\cfrac{\overline c}{w_D}=2\pi\cfrac{\overline c}{2\pi\overline c(3\rho/4\pi)^{1/3}}=(\cfrac{4\pi}{3})^{1/3}\rho^{-1/3}$$

德拜波长和格点间的距离在同一个数量级，差别不大。
(b) 已知能量的表达式

$$E=9NkT(\cfrac{T}{T_D})^3\int_0^{T_D/T}\cfrac{x^3dx}{e^x-1}$$
对于高温情况，有$T>>T_D\implies T_D/T\to0$，所以公式中的积分的被积函数可以化为$\cfrac{x^3}{1+x-1}=x^2$,所以积分的结果为$\cfrac 13(T_D/T)^3$，能量为 $$E=3NkT$$
可以看到高温情况下能量和温度成正比；
在低温情况下$T<<T_D\implies T_D/T\to\infty$,积分项的积分范围从0延伸到无穷大，由 $$\int_0^{\infty}\cfrac{x^3dx}{e^x-1}=\Gamma(4)\zeta(4)=6\times\cfrac{\pi^2}{90}=\cfrac{\pi^2}{15}$$
所以能量为 $$E=\cfrac{\pi^2}{15}·9NkT(\cfrac{T}{T_D})^3=\cfrac{3\pi^2Nk}{5T_D^3}T^4$$
(d) 在二维情况下态密度为$g(w)dw=\cfrac{Aw}{2\pi c^2}dw$
所以能量为 $$\begin{align} E&=\int_0^{w_D}\hbar w\overline n(w)g(w)dw\\&=\cfrac{\hbar A}{2\pi c^2}\int_0^{w_D}\cfrac{w^2dw}{e^{\beta\hbar w}-1}=\cfrac{\hbar A}{2\pi c^2}(\cfrac{kT}{\hbar})^3\int_0^{T_D/T}\cfrac{x^2dx}{e^x-1}\\&=\begin{cases}1.202\cfrac{\hbar A}{\pi c^2}(\cfrac{kT}{\hbar})^3,T<<T_D\\\cfrac{k^3\hbar T_D^2A}{4\pi c^2}T,T>>T_D\end{cases} \end{align}$$
热容为 $$C_V=(\cfrac{\partial E}{\partial T})_V=\begin{cases}3.606\cfrac{\hbar A}{\pi c^2}(\cfrac{k}{\hbar})^3T^2,T<<T_D\\\cfrac{k^3\hbar T_D^2A}{4\pi c^2},T>>T_D\end{cases}$$
在一维情况下，$g(w)=\cfrac{L}{\pi c}dw$
所以能量为 $$\begin{align} E&=\int_0^{w_D}\hbar w\overline n(w)g(w)dw\\&=\cfrac{\hbar L}{\pi c}\int_0^{w_D}\cfrac{wdw}{e^{\beta\hbar w}-1}=\cfrac{\hbar L}{\pi c}(\cfrac{kT}{\hbar})^2\int_0^{T_D/T}\cfrac{xdx}{e^x-1}\\&=\begin{cases}\cfrac{\pi Lk^2}{6 c\hbar}T^2, T<<T_D\\\cfrac{\hbar Lk^2T_D}{\pi c}T, T>>T_D\end{cases} \end{align}$$
热容为 $$C_V=(\cfrac{\partial E}{\partial T})_V=\begin{cases}\cfrac{\pi Lk^2}{3 c\hbar}T, T<<T_D\\\cfrac{\hbar Lk^2T_D}{\pi c}, T>>T_D\end{cases}$$

Problem 6.36. Relation of Tc to the zero-point energy
当$\mu=0$时，

$$\rho=\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}\int_0^{\infty}\cfrac{x^{1/2}dx}{e^x-1}=2.612\cfrac{\sqrt{\pi}}{2}\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}$$
$$E=\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}kT_c\int_0^{\infty}\cfrac{x^{3/2}dx}{e^x-1}=1.341\cfrac{3\sqrt{\pi}}{4}\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}$$
两式相除，得到 $$\cfrac{E}{\rho}=\cfrac{3\times1.341}{2\times2.612}kT_c=0.77kT_c$$
若将粒子至于体积为$a^3=1/\rho$的区域中，则 $$T_c=\cfrac{E}{0.77ka^3}$$

Problem 6.37. Numerical evaluation of µ for an ideal Bose gas
因为

$$\rho=\cfrac{(2m)^{3/2}}{4\pi^2\hbar^3}\int_0^{\infty}\cfrac{{\epsilon}^{1/2}d\epsilon}{e^{\beta(\epsilon-\mu)}-1}$$
作变量代换$\epsilon=kT_cy,T=T_cT^*,\mu=kT_c\mu^*$，得到 $$\rho=\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}\int_0^{\infty}\cfrac{y^{1/2}dy}{e^{(y-\mu^*)/T^*}-1}$$
又经计算得到 $$\rho=2.612\cfrac{\sqrt{\pi}}{2}\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3},$$
两式相除，得到想要的结果： $$1=\cfrac{2}{2.612\sqrt{\pi}}\int_0^{\infty}\cfrac{y^{1/2}dy}{e^{(y-\mu^*)/T^*}-1}\tag{6.211}$$

Problem 6.38.
由Problem6.36中给出的密度的表达式可以得到

$$\begin{align} \rho_c&=2.612\cfrac{\sqrt{\pi}}{2}\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}=2.612(\cfrac{2 mkT_c}{2\pi\hbar^2})^{3/2}=\cfrac{2.612}{\lambda^3}. \end{align}$$
因为系统的平均粒子数随温度改变，系统的体积不变，所以给定一个温度，可以产生一个相应的密度$\rho_c$.

Problem 6.39.
因为$\rho=\cfrac{2.612}{\lambda^3},$可以得到$\lambda=(\cfrac{2.612}{\rho})^{1/3}$
而粒子间的平均间隔为$\rho^{-1/3}$,所以在$T=T_c$时，热德布罗意波长和粒子间平均距离是可以比拟的

Problem 6.40. Temperature dependence of the pressure
(a) 对于理想玻色气体，$T<T_c$时，对压强有贡献的那部分粒子数为有效粒子数，其为

$$N_{eff}=N(\cfrac{T}{T_c})^{3/2}$$ 将其代入气压状态方程得到： $$P=\cfrac{NkT^{5/2}}{VT_c^{3/2}}$$ 可以看到，在低温条件下$P ∝ T ^{5/2}$
(b) $$\Omega=-P_0V=kT\ln(1-e^{\beta\mu})$$
所以基态对压强的贡献为： $$P_0=\cfrac{kT}{V}\ln\cfrac{1}{1-e^{\beta\mu}}=\cfrac{kT}{V}\ln\left(\cfrac{1}{e^{-\beta\mu}-1}+1\right)$$
即 $$P_0=\cfrac{kT}{V}\ln\left(\overline N_0+1\right).$$
在低温情况下其趋于0，在$T<T_c$时，$\overline N_0$很大，P0和V无关。

Problem 6.41. Estimate of the Bose condensation temperature
(a)

$$\begin{align} T_c&=\cfrac{1}{2.612^{2/3}}\cfrac{2\pi\hbar^2}{mk}\rho^{2/3}=1.004\times10^{-17}K \end{align}$$
(b) $$\begin{align} \rho_c&=2.612\cfrac{\sqrt{\pi}}{2}\cfrac{(2mkT_c)^{3/2}}{4\pi^2\hbar^3}=5.9\times10^{19}m^{-3}. \end{align}$$
所以粒子间的平均距离为： $$d=\rho^{-1/3}=2.569\times10^{-7}m.$$
Problem 6.42. Number fluctuations
$$P_s=\cfrac 1{Z_G}e^{-\beta(E_s-\mu N_s)}$$
其中$Z_G=\sum_s e^{-\beta(E_s-\mu N_s)}$,所以粒子数平均值为 $$\overline N=\sum_sN_sP_s=\cfrac {\sum_sN_s e^{-\beta(E_s-\mu N_s)}}{\sum_s e^{-\beta(E_s-\mu N_s)}}$$
所以 $$\begin{align} \left(\cfrac{\partial \overline N}{\partial\mu}\right)_{T,V}&=\cfrac{1}{kT}\left(\overline{N^2}-\overline N^2\right) \end{align}$$

Problem 6.43. Another Maxwell relation
(a)

$$\begin{align} \mu&=\left(\frac{\partial F}{\partial N}\right)_{T,V}=\frac{\partial }{\partial N}(Nf)=f+\rho\left(\frac{\partial f}{\partial \rho}\right)_T \end{align}$$

$$\begin{align} \left(\frac{\partial \mu}{\partial \rho}\right)_{T}&=\left(\frac{\partial f}{\partial \rho}\right)_T+\rho\left(\frac{\partial f}{\partial \rho}\right)_T+\left(\frac{\partial^2 f}{\partial \rho^2}\right)_T=2\left(\frac{\partial f}{\partial \rho}\right)_{T}+\rho\left(\frac{\partial^2 f}{\partial \rho^2}\right)_{T} \end{align}$$

$$\begin{align} P&=-\left(\frac{\partial F}{\partial N}\right)_{T,N}=-N\left(\frac{\partial f}{\partial \rho}\right)_{T}\frac{\partial \rho}{\partial V}=\frac{N^2}{V^2}\left(\frac{\partial f}{\partial \rho}\right)_{T}=\rho^2\left(\frac{\partial f}{\partial \rho}\right)_{T} \end{align}$$

$$\begin{align} \left(\frac{\partial P}{\partial \rho}\right)_{T}&=2\rho\left(\frac{\partial f}{\partial \rho}\right)_{T}+\rho^2\left(\frac{\partial^2 f}{\partial \rho^2}\right)_{T}=\rho\left(\frac{\partial \mu}{\partial \rho}\right)_{T} \end{align}$$
(b) $$\begin{align} \left(\frac{\partial P}{\partial \rho}\right)_{T}&=\left(\frac{\partial P}{\partial V}\right)_{T,N}\frac{\partial V}{\partial \rho}=\left(\frac{\partial P}{\partial V}\right)_{T,N}\frac{\partial }{\partial \rho}\left[\cfrac{N}{\rho}\right]=-\cfrac{N}{\rho^2}\left(\frac{\partial P}{\partial V}\right)_{T,N}=-\cfrac{V^2}{N}\left(\frac{\partial P}{\partial V}\right)_{T,N} \end{align}$$

$$\begin{align} \left(\cfrac{\partial \mu}{\partial \rho}\right)_{T}&=\left(\cfrac{\partial \mu}{\partial N}\right)_{T}\cfrac{\partial N}{\partial \rho}=\left(\cfrac{\partial \mu}{\partial N}\right)_{T}\cfrac{\partial }{\partial \rho}\left(\rho V\right)=V\left(\cfrac{\partial \mu}{\partial N}\right)_{T,V}. \end{align}$$
(c) 由(a)中最后一个式子和(b)中的两个关系式得到：
$$V\left(\cfrac{\partial \mu}{\partial N}\right)_{T,V}=-\cfrac{V^2}{N}\left(\cfrac{\partial P}{\partial V}\right)_{T,N}$$
所以 $$\begin{align} N\left(\cfrac{\partial \mu}{\partial N}\right)_{T,V}&=-\cfrac 1{\rho}\cfrac NV\cfrac{V^2}{N}\left(\cfrac{\partial P}{\partial V}\right)_{T,N}=-\cfrac V{\rho}\left(\cfrac{\partial P}{\partial V}\right)_{T,N}=\cfrac{1}{\rho\kappa} \end{align}$$
又由式(6.228)有：$\left(\cfrac{\partial \overline N}{\partial\mu}\right)_{T,V}=\cfrac{1}{kT}\left(\overline{N^2}-\overline N^2\right)$
所以： $$\rho\kappa N=\cfrac{1}{kT}\left(\overline{N^2}-\overline N^2\right)$$

$$\kappa=\cfrac{1}{kT\rho}\cfrac{\left(\overline{N^2}-\overline N^2\right)}{\overline N}.$$