@xzyxzy
2018-10-18T12:20:21.000000Z
字数 1917
阅读 1975
[JLOI2015]骗我呢
题解
作业部落
评论地址
TAG:数学,DP
题意
骗你呢
求满足以下条件的的矩阵的个数对取模
对于矩阵中的第行第列的元素都有
题解
Part 0 前言
不会做啊!(杠了四五个小时!)
谢两位dalao:blog1、blog2
以下图片均来自于此篇文章:http://www.cnblogs.com/coco-night/p/9552677.html,如有冒犯请与我联系,谢谢!
Part 1 朴素DP
首先发现一个很好的性质:
每行是递增的并且一行个元素,取值只能在中选
那么必然该行至多有一个位置与后一个位置相差2,其余的都只相差1
由此可以列出一个简单的:
表示第行没有出现过的数是的方案数
至于上界为什么是可以手动模拟一下,假设这行没有出现过,上一行试一试、、、,发现大于的就不合法了
略微优化一下就变成了
Part 2 转化为图形
发现这个像极了组合数公式,把它套用在坐标系里就是这个样子
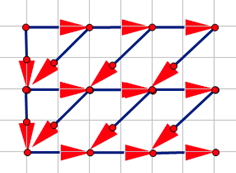
自上而下第行,从左往右第列的点就表示,其指向的点就表示可以转移
这样仍然不太好处理,我们继续转化:
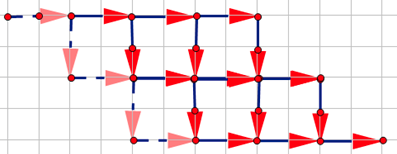
还是不好看,给它对称一下:
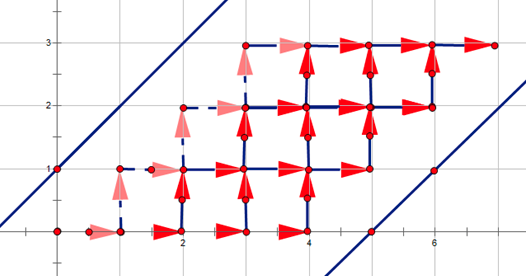
Part 3 挖掘组合意义
这么一看,不就是从原点出发,只能向右或向上走,不接触直线A,B,到达点(n+m+1,n)的路径条数吗!
直线,直线
Part 4 计算
这种格路数计算(如两双手)都可以考虑采用容斥计数
不考虑其他限制,原点到的方案数是
考虑不合法方案是什么:如依次经过
把它缩一下:
可以发现不合法方案要么以开头要么以开头
表示为首次跨越的直线是还是
所以:答案=总方案数 - A开头的方案数 - B开头的方案数
,把沿对称得到
每条从到的路径都依次对应一条以A结尾或者以AB结尾的路径!
如图:(这个图是我自己画的!)

上面是一条以结尾的路径

上面是一条以结尾的路径
所以,总共的不合法方案是
- A
- B
- AB
- BA
- ABA
- BAB
- ABAB
- BABA
- ...
为了减去以开头的方案,需要减去以A,AB结尾的方案,加上以BA,BAB结尾的方案,减去....
那么实现方式是:把(x,y)沿A翻折,减去答案;将翻折过的点沿B翻着,加上答案;再沿A翻折...
同理计算以开头的方案,就是先沿折就好了
具体细节的话沿着折是,沿着折是
完美解决本题!
代码
#include<iostream>using namespace std;const int P=1e9+7,N=3e6+10;int n,m,up,inv[N],jc[N],inj[N];int Calc(int x,int y) {return (x<0||y<0)?0:1ll*jc[x+y]*inj[x]%P*inj[y]%P;}void flip1(int &x,int &y) {swap(x,y);x--;y++;}void flip2(int &x,int &y) {swap(x,y);x+=m+2;y-=m+2;}void add(int &x,int y) {x+=y;if(x>=P) x-=P;}int main(){cin>>n>>m;inv[0]=inv[1]=jc[0]=inj[0]=1;up=max(n,m)*3+1;for(int i=2;i<=up;i++) inv[i]=(P-1ll*P/i*inv[P%i]%P)%P;for(int i=1;i<=up;i++) jc[i]=1ll*jc[i-1]*i%P,inj[i]=1ll*inj[i-1]*inv[i]%P;int x=n+m+1,y=n,ans=Calc(x,y);while(x>=0&&y>=0){flip1(x,y);add(ans,P-Calc(x,y));flip2(x,y);add(ans,Calc(x,y));}x=n+m+1,y=n;while(x>=0&&y>=0){flip2(x,y);add(ans,P-Calc(x,y));flip1(x,y);add(ans,Calc(x,y));}return cout<<ans<<endl,0;}
