广义后缀自动机

字符串 题解

作业部落

评论地址

一、前言

广义后缀自动机实际上考得比普通后缀自动机要更多更灵活
所以这里作为一个小专题呈现，题单在后缀自动机的总题单里
为了更好掌握广义$SAM$，这里提供一个高级模板题的题解

二、构建方法

普通后缀自动机处理单串的问题，多串就只能使用广义$SAM$了

最方便的构建

一种方案是把字符串中间依次用从未出现过的字符连接，当作一个字符串处理，再多几个特判

    for(int i=1;i<=m;i++)
    {
        string A; cin>>A; s[++l]='#';
        for(int j=0,l=A.size();j<l;j++) s[++l]=A[j];
    }

一种方案是每插入一个串就把$lst=1$，其余什么都不用改变

    for(int i=1;i<=m;i++)
    {
        lst=1; cin>>s; l=s.size();
        for(int j=0;j<l;j++) Extend(s[j]-'0');      
    }

最准确的构建

其实准确来说，广义后缀自动机是通过遍历Trie树建的，所以要先建好$Trie$树
每次找到$fa[x]$的节点作为$lst$往后接即可

有两种方法：$BFS$与$DFS$遍历建后缀自动机
叶大佬告诉我们，$DFS$会被卡成$n^2$而$BFS$不会，就像下面图片中的例子

int Extend(int f,int c)
{
    if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];//？！
    int p=++node,ff=0;lst=p;
    len[p]=len[f]+1;
    while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
    if(!f) {fa[p]=1;return p;}
    int x=ch[f][c],y=++node;
    if(len[x]==len[f]+1) {fa[p]=x;node--;return p;}
    if(len[p]==len[f]+1) ff=1;//？！
    memcpy(ch[y],ch[x],sizeof(ch[y]));
    len[y]=len[f]+1; fa[y]=fa[x]; fa[x]=fa[p]=y;
    while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];//原因就在这
    return ff?y:p;
}

你会发现这和后缀自动机的模板有些区别诶
首先是有一个返回值，这个很好理解，返回的是如果下次要往后接的$lst$，也就是方便找到$Trie$树某点在$SAM$上的位置，直接传进来就好啦
然后是有一个if(len[p]==len[f]+1) return y;的特判
前面也有一个if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];的特判

好，广义$SAM$的构建就讲完了
什么？！WTF？！那个特判是啥意思我还不造嘞！
别急，我们来通过例题理解它

三、例题

链接：HN省队集训
题意：给$n$个字符串$s$，强制在线进行$4$个操作，询问/串长$1e5$，$n\le20$

题解
对于操作$1$
记录$pos[i][j]$表示在第$i$次操作后$j$号串的结尾字符在$SAM$上的节点编号是$j$，当在第$i$次操作在字符串$x$后插入字符时，令$lst=pos[i-1][x]$，然后照常插入即可

对于操作$2$
记录$siz[i][j]$表示在$i$号点，由$j$号字符串贡献的$Endpos$集合的大小，实际意义就是$i$号点代表的字符串集合在$n$个串中共出现了$\sum_{k=1}^{n}siz[i][j]$，其中在$j$号串中出现了$siz[i][j]$次。
查询$z$串中$x$串的出现次数，那么$x$串在$y$次操作后的结尾位置是$pos[y][x]$，那么$siz[pos[y][x]][z]$就是答案。
这里的$siz$是在$parent$树上对子树进行求和才有上述意义，原理可见于我的另一篇博文后缀自动机，但是这里需要在线插入节点，于是我们用$lct$维护$parent$树上的$siz$，每次断开或者连上父亲的时候相当是给节点到$parent$根的路径$+/-1$，所以这里的$lct$只需要支持链加，不需要改变树的根所以没有$makeroot$、$reverse$等操作，如果需要学习$lct$，可见我的另一篇博文lct

对于操作$3$
维护一个全局变量$sum$，每个节点贡献的本质不同的子串个数就是$len[x]-len[fa[x]]$

对于操作$4$
在$SAM$上匹配到T的结束位置的节点，$Ans=max(siz[pos][i]),i=1..n$

复杂度分析
操作$1$的总复杂度是$\sum len[s_i]×log(n)$的，操作$2$是$log(n)$的，操作$2$是$O(1)$，操作$4$是$\sum len[T_i]+20$的，$log$都是$lct$的复杂度
所以总共时间复杂度是$O(\sum len[s_i]*log(n)+\sum len[T_i])$的
空间复杂度$O(n*20)$左右

代码如下

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define ll long long
using namespace std;
int read()
{
    char ch=getchar();int h=0,t=1;
    while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
    if(ch=='-') t=-1,ch=getchar();
    while(ch>='0'&&ch<='9') h=h*10+ch-'0',ch=getchar();
    return h*t;
}
const int N=1e6+100;
char s[N];
int n,zx,m,ans,node=1;
int fa[N],ch[N][11],len[N],pos[N][21];
ll sum;
namespace lct
{
    #define lc t[x].ch[0]
    #define rc t[x].ch[1]
    struct LCT{int fa,ch[2],val[21],tag[21];}t[N];
    int isrt(int x) {return t[t[x].fa].ch[0]!=x&&t[t[x].fa].ch[1]!=x;}
    void Tag(int x,int y,int k) {t[x].val[y]+=k; t[x].tag[y]+=k;}
    void pushdown(int x)
    {
        for(int i=1;i<=n;i++)
        {
            if(!t[x].tag[i]) continue;
            if(lc) Tag(lc,i,t[x].tag[i]);
            if(rc) Tag(rc,i,t[x].tag[i]);
            t[x].tag[i]=0;
        }
    }
    void rotate(int x)
    {
        int y=t[x].fa,z=t[y].fa;
        int k=t[y].ch[1]==x;
        if(!isrt(y)) t[z].ch[t[z].ch[1]==y]=x; t[x].fa=z;
        t[y].ch[k]=t[x].ch[k^1];               t[t[x].ch[k^1]].fa=y;
        t[x].ch[k^1]=y;                        t[y].fa=x;       
    }
    void Push(int x){if(!isrt(x)) Push(t[x].fa);pushdown(x);}
    void splay(int x)
    {
        Push(x);
        while(!isrt(x))
        {
            int y=t[x].fa,z=t[y].fa;
            if(!isrt(y)) (t[z].ch[0]==y)^(t[y].ch[0]==x)?rotate(x):rotate(y);
            rotate(x);
        }
    }
    void Access(int x) {for(int y=0;x;y=x,x=t[x].fa) splay(x),rc=y;}
    void Add(int x,int y,int op) {for(int i=1;i<=n;i++) Tag(x,i,t[y].val[i]*op);}
    void link(int x,int y) {Push(x);t[x].fa=y;Access(y);splay(y);Add(y,x,1);}
    void cut(int x) {Access(x);splay(x);Add(lc,x,-1);lc=t[lc].fa=0;}
    int query(int x,int k) {Push(x);return t[x].val[k];}
}
int Extend(int f,int id,int c)
{
    if(ch[f][c]&&len[ch[f][c]]==len[f]+1)
    {
        int p=ch[f][c];
        lct::Access(p);lct::splay(p);lct::Tag(p,id,1);
        return p;
    }
    int p=++node; len[p]=len[f]+1; lct::t[p].val[id]=1;
    while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
    if(!f) {fa[p]=1;lct::link(p,1);sum+=len[p]-len[fa[p]];return p;}
    int x=ch[f][c];
    if(len[f]+1==len[x]) {fa[p]=x;lct::link(p,x);sum+=len[p]-len[fa[p]];return p;}
    if(len[f]+1==len[p])//！！
    {
        lct::cut(x);lct::link(p,fa[x]);lct::link(x,p);
        memcpy(ch[p],ch[x],sizeof(ch[p]));
        fa[p]=fa[x]; fa[x]=p;
        sum-=len[p]-len[fa[p]];
        while(f&&ch[f][c]==x) ch[f][c]=p,f=fa[f];
    }
    else
    {
        int y=++node; len[y]=len[f]+1;
        lct::cut(x);lct::link(y,fa[x]);lct::link(x,y);lct::link(p,y);
        memcpy(ch[y],ch[x],sizeof(ch[y]));
        fa[y]=fa[x]; fa[x]=fa[p]=y;
        while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
    }
    sum+=len[p]-len[fa[p]];
    return p;
}
int calc()
{
    int x=1,res=0,i,l; scanf("%s",s+1);
    for(i=1,l=strlen(s+1);i<=l&&x;i++) x=ch[x][s[i]-'0'];
    if(i!=l+1) return 0;
    lct::Push(x);
    for(i=1;i<=n;i++) res=max(res,lct::t[x].val[i]);
    return res;
}
int main()
{
    n=read();zx=read();
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1); pos[0][i]=1;
        for(int p=1,l=strlen(s+1);p<=l;p++)
            pos[0][i]=Extend(pos[0][i],i,s[p]-'0');
    }
    m=read();
    for(int i=1;i<=m;i++)
    {
        int op=read(),x,y,z;
        for(int p=1;p<=n;p++) pos[i][p]=pos[i-1][p];
        if(op<=2) x=read(),y=read();
        if(op==1) y=(y^(ans*zx))%10,pos[i][x]=Extend(pos[i][x],x,y);
        else if(op==2) z=read(),printf("%d\n",ans=lct::query(pos[y][x],z));
        else if(op==3) printf("%lld\n",sum);
        else printf("%d\n",ans=calc());
    }
    return 0;
}

Wait！
出题人和我讲这道题的时候，特别强调要特判！
但是我一直不理解，把特判if(len[f]+1==len[p]) ff=1;删了后还是过了本题
于是他给了一组$hackdata$并且在$BZOJ$加强了数据

Input
2 0
3201
01
1
2 2 0 1
Output
Right : 1
Wrong : 0

首先我们建出第一个串的$SAM$（黑边是$SAM$上的边，基佬紫边是$Parent$树上的边）

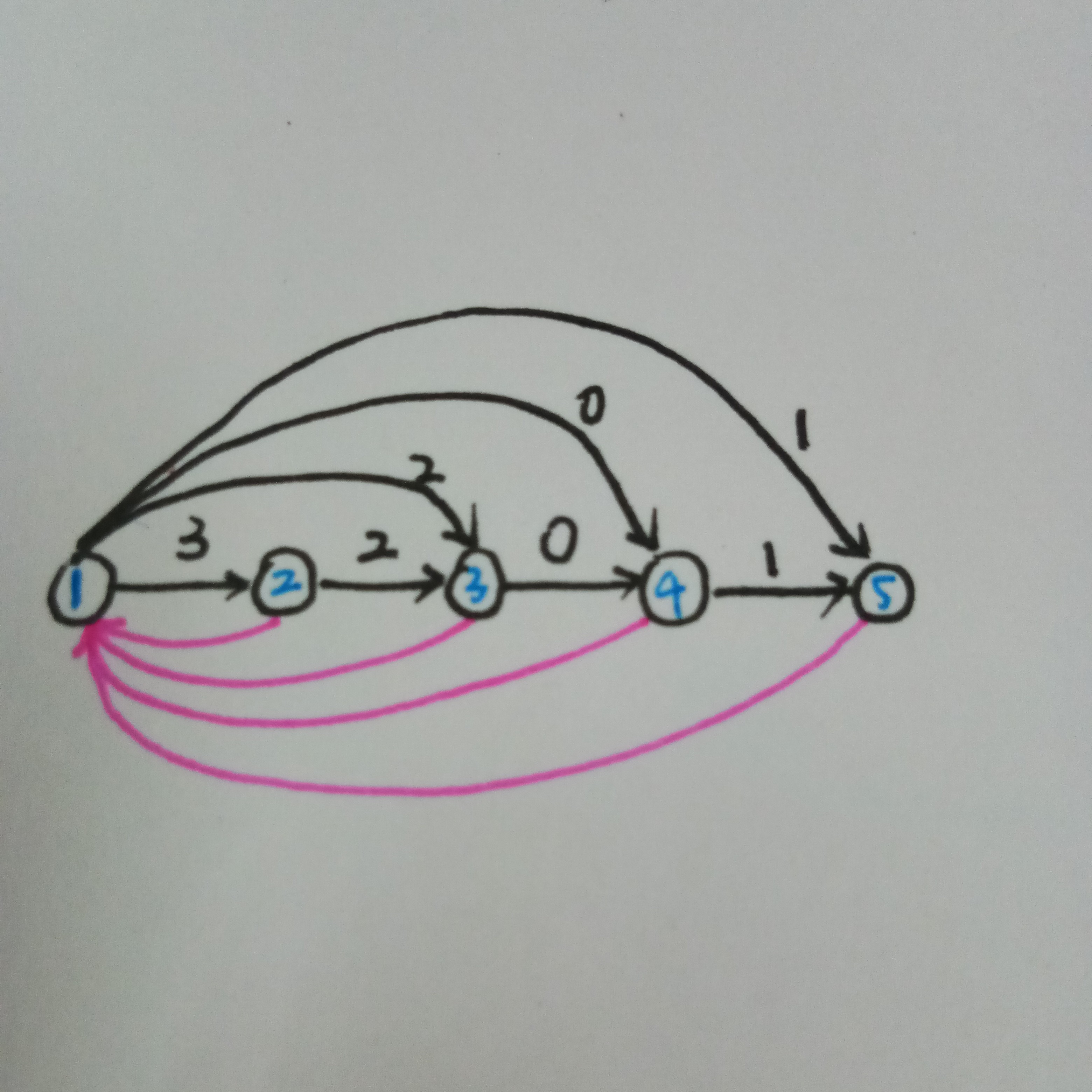
我们先加特判，那么继续建就会这样（姨妈红边是删去的边）

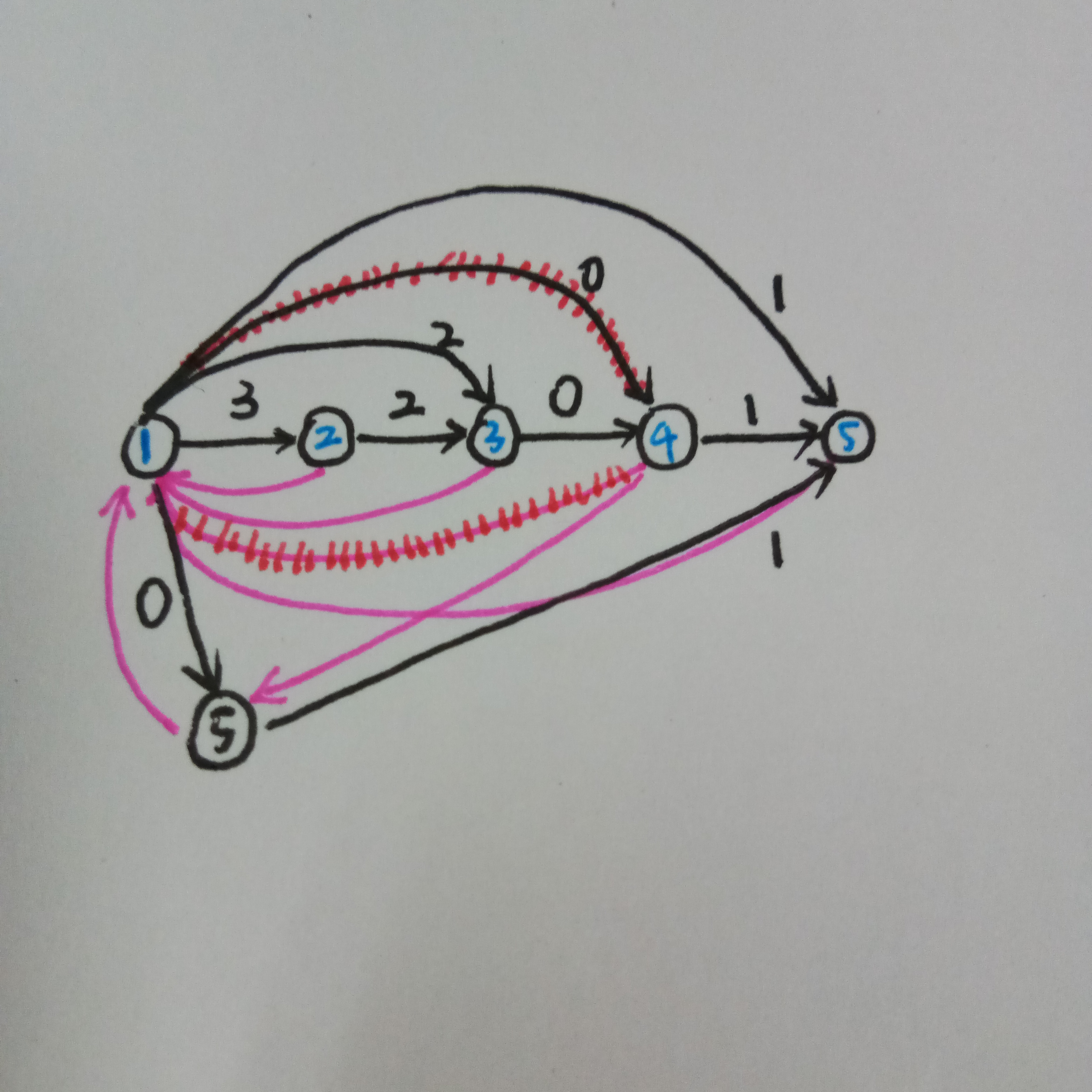
继续加边

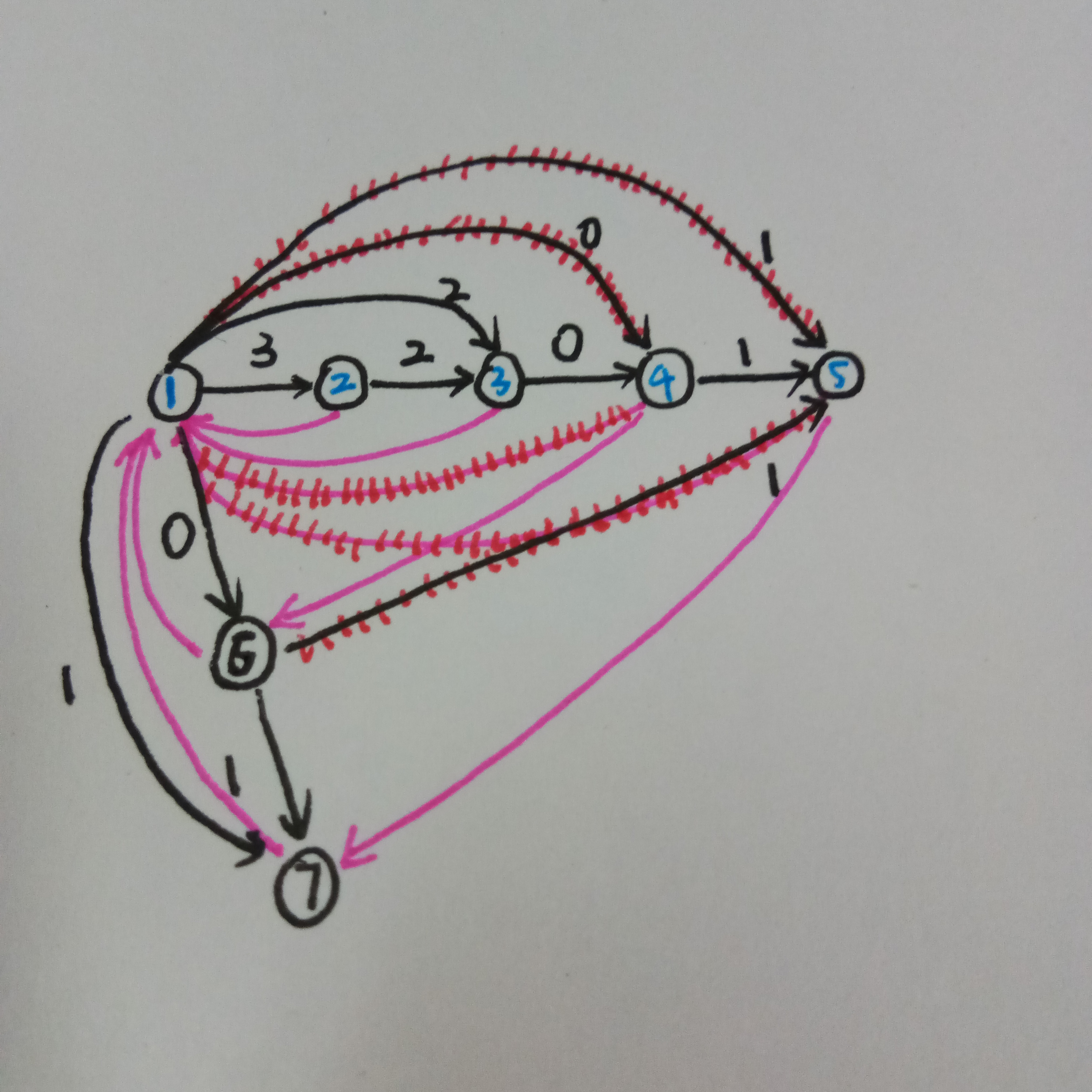
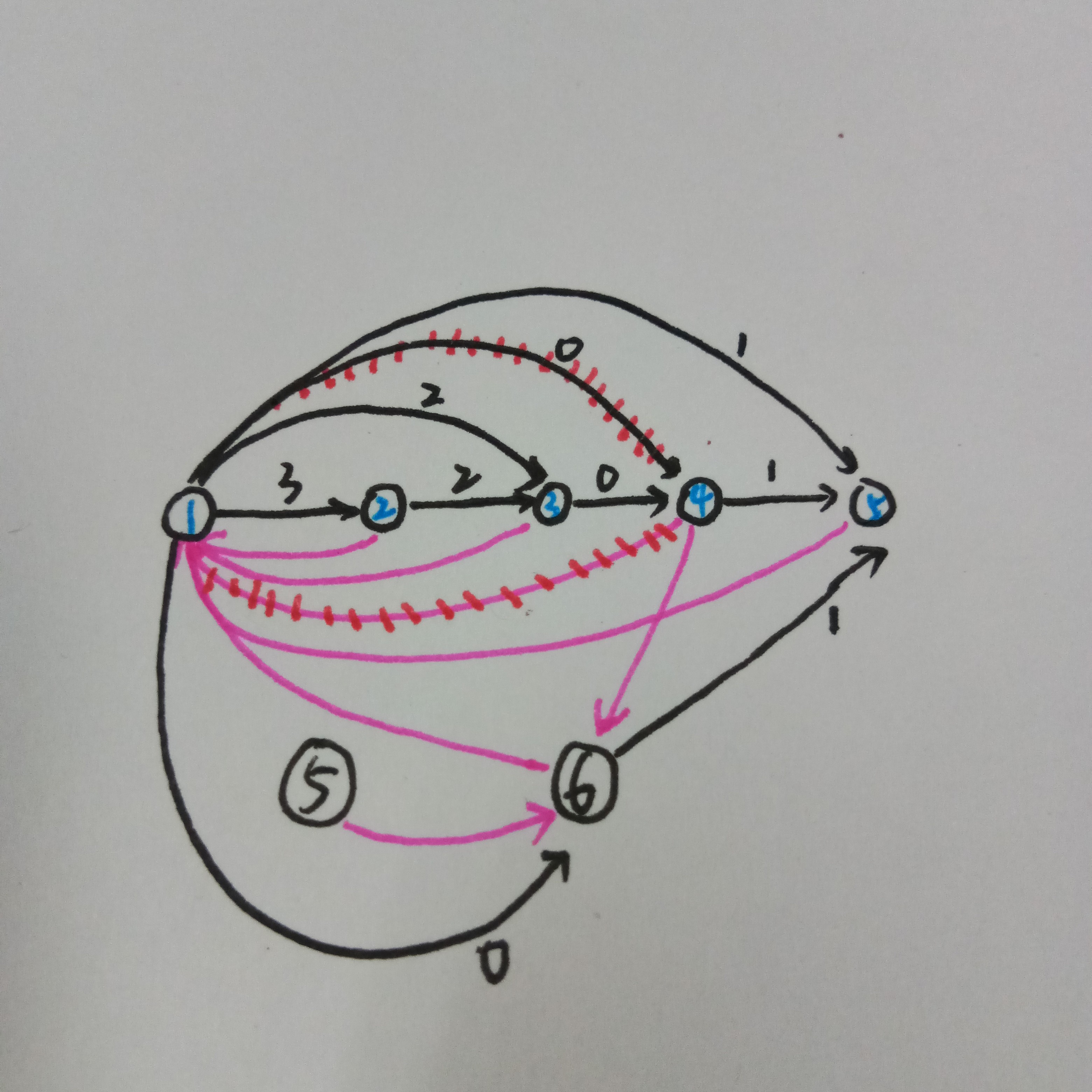
但是如果不加这个特判，就会撒夫夫地把蓝$4$给复制一边，但是这时第二个串的$0$的结尾位置是$5$，当我查询$2$串在$1$串中出现次数就会访问到$siz[pos[x][2]][1]$，此时很遗憾地发现调用到了$5$节点，它没有记录蓝$4$的信息

这样写代码很长，有没有一种简单的写法捏？
有的，我们发现黑$5$不会再被访问到，相当于他的贡献被算到了六号点上，同时又没有点指向它所以它不会被访问到。对比上面两张图，我们发现其实就是$图1$中的黑$5$和$图3$中的黑$6$是完全一样的诶！
于是直接返回黑$6$就好啦
把上述代码的$Extend$改成下面这种

int Extend(int f,int id,int c)
{
    if(ch[f][c]&&len[ch[f][c]]==len[f]+1)
    {
        int p=ch[f][c];
        lct::Access(p);lct::splay(p);lct::Tag(p,id,1);
        return p;
    }
    int p=++node,ff=0; len[p]=len[f]+1; lct::t[p].val[id]=1;
    while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
    if(!f) {fa[p]=1;lct::link(p,1);sum+=len[p]-len[fa[p]];return p;}
    int x=ch[f][c];
    if(len[f]+1==len[x]) {fa[p]=x;lct::link(p,x);sum+=len[p]-len[fa[p]];return p;}
    if(len[f]+1==len[p]) ff=1;
    int y=++node; len[y]=len[f]+1;
    lct::cut(x);lct::link(y,fa[x]);lct::link(x,y);lct::link(p,y);
    memcpy(ch[y],ch[x],sizeof(ch[y]));
    fa[y]=fa[x]; fa[x]=fa[p]=y;
    while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
    sum+=len[p]-len[fa[p]];
    return ff?y:p;
}

是不是很方便？

从本质上分析这两个特判

if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];

我们建$SAM$是在$Trie$树上遍历建的，这句话表示访问到$Trie$树上一个点，它在$SAM$上已经被建出来了，所以不需要新建

if(len[f]+1==len[p]) ff=1;

这句特判起作用的条件是中间$f$没有被改变，也就是说存在$ch[f][c]$，假设$f$表示的字符串是$A$，那么插入字符$c$后产生$Ac$，但是$Ac$已经存在于自动机上，所以要把它从原来的状态剥离出来，复制一遍，从后来的操作中可以发现最后我们需要的$lst$也就是$return$的点应该是复制出来的那个点