@xzyxzy 2018-04-11T07:19:16.000000Z 字数 2862 阅读 1723

主席树

数据结构

作业部落链接：https://www.zybuluo.com/xzyxzy/note/1085441

一、概述

~~YL讲的主席树专题orz~~
主席树是可持久化线段树的一种
主席树可以查询历史版本
实现方式就是每次修改就相当于在历史的长河中加入那棵被修改了的树
查询连续的一段历史修改操作结果，就在漫漫长河中寻找就好了

所以为了降低时间复杂度，维护前缀和
为了降低空间复杂度，就这样子(图片来源于此博客)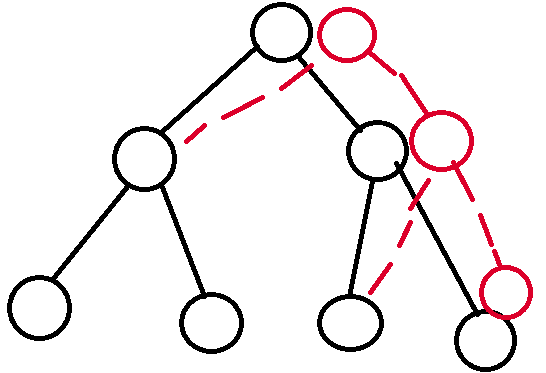 此处输入图片的描述
这样子每修改一次加 $logN$ 个点，既保证时间复杂度又保证空间复杂度，是不是很妙啊

二、题单

三、套路

又到最激动人心的时刻了，通常博主为了总结套路需要刷大量的变态题死上万个脑细胞了，今天多亏了 $YL$ 的完美讲课

1、查询历史版本

除了模板外，大概没有这类题了吧
[luogu]可持久化数组模板

2、查询区间Kth

模板吧 [Luogu3834]可持久化线段树
可以查询区间中位数（第总数 $/2$ 大）
同理查询区间前 $k$ 大的数的和

3、树上路径Kth

每个点维护从该点到根的路径的链（扔进权值线段树里）
那么查询就是 $u+v-lca(u,v)-fa[lca(u,v)]$
[SPOJ10628]Count On a Tree

4、二维数点问题

把主席树看成一个象限，以操作版本为横轴，插入全值为纵轴，就可以进行查询操作版本在 $(l,r)$ ，权值在 $(u,d)$ 之间的最值或数量
这种方法是树套树的思想，主席树完成会很方便，常作为工具用于优化DP等

5、区间内不重复（重复次数不超过ｋ）的数的个数

每个点维护值域线段树，该点插入的 $val$ 为该数前1次（k次）出现的位置，那么进行二维数点，查询当前位置在 $(l,r)$ 且前1次（k次）位置在 $(l,r)$ 的点的个数，这些点是不计入贡献的，用总点数减去即为答案
CF813E Army Creation

6、二分转化为0/1求值

一些题需要求最值的时候，自然地会想到二分，二分后将大于mid的置为1，小于的置为0或-1，很多时候会使问题方便求解很多
想办法用主席树维护这个过程
将点按照权值排序，对于每个点（即每个权值，但是相同权值有可能开多棵树）开一棵位置线段树，将上一个点的位置置为0或-1，那么二分下来之后就直接在该位置的线段树上进行操作就好了
CF484E Sign on Fence

7、更多神奇的套路...

数据结构的套路是发掘不尽的，只要深刻理解题意，所需要的数据结构就会自己找上门来，同时灵活处理好正序倒序，分清楚权值还是位置，才能见题拆题

代码

[luogu]可持久化数组模板
要求一种能够查询历史版本的数据结构
通常情况主席树可以不用建0树，有些特殊情况建0会方便很多比如说这个
主要还是看个人习惯吧

注意：Query(Root[r],Root[l-1]...)易错打成Query(r,l-1...)

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int read()
{
    char ch=getchar();int h=0,t=1;
    while(ch!='-'&&(ch>'9'||ch<'0'))ch=getchar();
    if(ch=='-')t=-1,ch=getchar();
    while(ch>='0'&&ch<='9'){h=h*10+ch-'0';ch=getchar();}
    return h*t; 
}
const int MAXN=1000100;
int N,M,Root[MAXN],tot;
struct Seg{int val,lc,rc;}t[MAXN*20];
inline void Get(Seg&A,Seg B){A.val=B.val,A.lc=B.lc,A.rc=B.rc;}
void Buildtree(int &now,int l,int r)
{
    Get(t[++tot],t[now]);now=tot;
    if(l==r){t[now].val=read();return;}
    int mid=(l+r)>>1;
    Buildtree(t[now].lc,l,mid);
    Buildtree(t[now].rc,mid+1,r);
}
void Replace(int &now,int l,int r,int pos,int v)
{
    Get(t[++tot],t[now]);now=tot;
    if(l==r){t[now].val=v;return;}
    int mid=(l+r)>>1;
    if(pos<=mid)Replace(t[now].lc,l,mid,pos,v);
    else Replace(t[now].rc,mid+1,r,pos,v);
}
int Query(int now,int l,int r,int pos)
{
    if(l==r)return t[now].val;
    int mid=(l+r)>>1;
    if(pos<=mid)return Query(t[now].lc,l,mid,pos);
    else return Query(t[now].rc,mid+1,r,pos);
}
int main()
{
    N=read();M=read();
    Buildtree(Root[0],1,N);
    for(int i=1;i<=M;i++)
    {
        int id=read(),op=read(),x=read(),y;
        Root[i]=Root[id];
        if(op==1){y=read();Replace(Root[i],1,N,x,y);}
        else printf("%d\n",Query(Root[i],1,N,x));
    }
    return 0;
}

后记

相信这篇文章除了题单外对主席树的学习没有一点帮助
安利一篇同样的看不懂的博客吧「Zctoylm」(反正我看不懂)
然后大佬们的水表「YCB」「ZSY」「YYB」「YL」「SYC」