Waves

未分类

Introduction

Wave is natual phenomenon in our world which has a close connection with musical instrumentsOne particular example is stand wave also known as a stationary wave – is a wave in a medium in which each point on the axis of the wave has an associated constant amplitude. The locations at which the amplitude is minimum are called nodes, and the locations where the amplitude is maximum are called antinodes.A more ideal wave is free wave which transport to place far away.

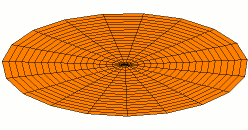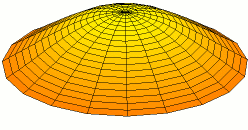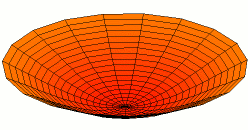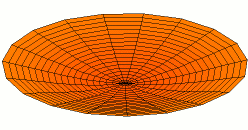
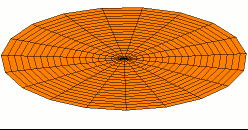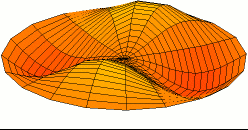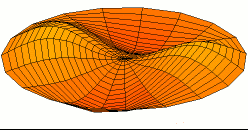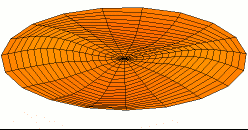
A standing wave on a circular membrane, an example of standing waves in two dimensions. This is the fundamental mode and A higher harmonic standing wave on a disk with two nodal lines crossing at the center.

A periodic travelling wave

Text

The ideal case

The central equation of wave motion is

$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$

y is the displacement of the string from its equilibrium form,x is distance measured along the horizontal direction,t is the time,and c is a parameter that turns out to be the speed with which a wave moves on the string.
we can deduce it from following analysis.

$\mu\Delta x\frac{d^2y_i}{dt^2}=Tsin\theta_{i+1}-Tsin\theta_{i}$
$sin\theta_i\approx\frac{y_{i}-y_{i-1}}{\Delta x}$
$\frac{d^2y_i}{dt^2}\approx=(\frac{T}{\mu})\frac{y_{i+1}-2y_{i}+y_{i-1}}{(\Delta x)^2}\approx(\frac{T}{\mu})\frac{\partial^2y}{\partial x^2}$

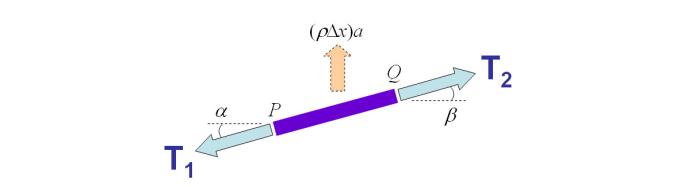
To construct a numerical approach to the wave equation,we write it in finite difference form.

$\frac{y(i,n+1)+y(i,n-1)-2y(i,n)}{(\Delta t)^2}\approx c^2[\frac{y(i+1,n)+y(i-1,n)-2y(i,n)}{(\Delta x^2)}]$

Rearranging it ,we express y(i,n+1) in term of y at previous time steps,with the result

$y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2[y(i+1,n)+y(i-1,n)]$

During the course of a calculation,the time index n will run from the initial time(n=0) to some final value corresponding to the time interval of interest.Sincd the string is modeled as a large number of discrete elements,I generate a lot of "data", but I only need to store information for 3 consecutive time step.
code1
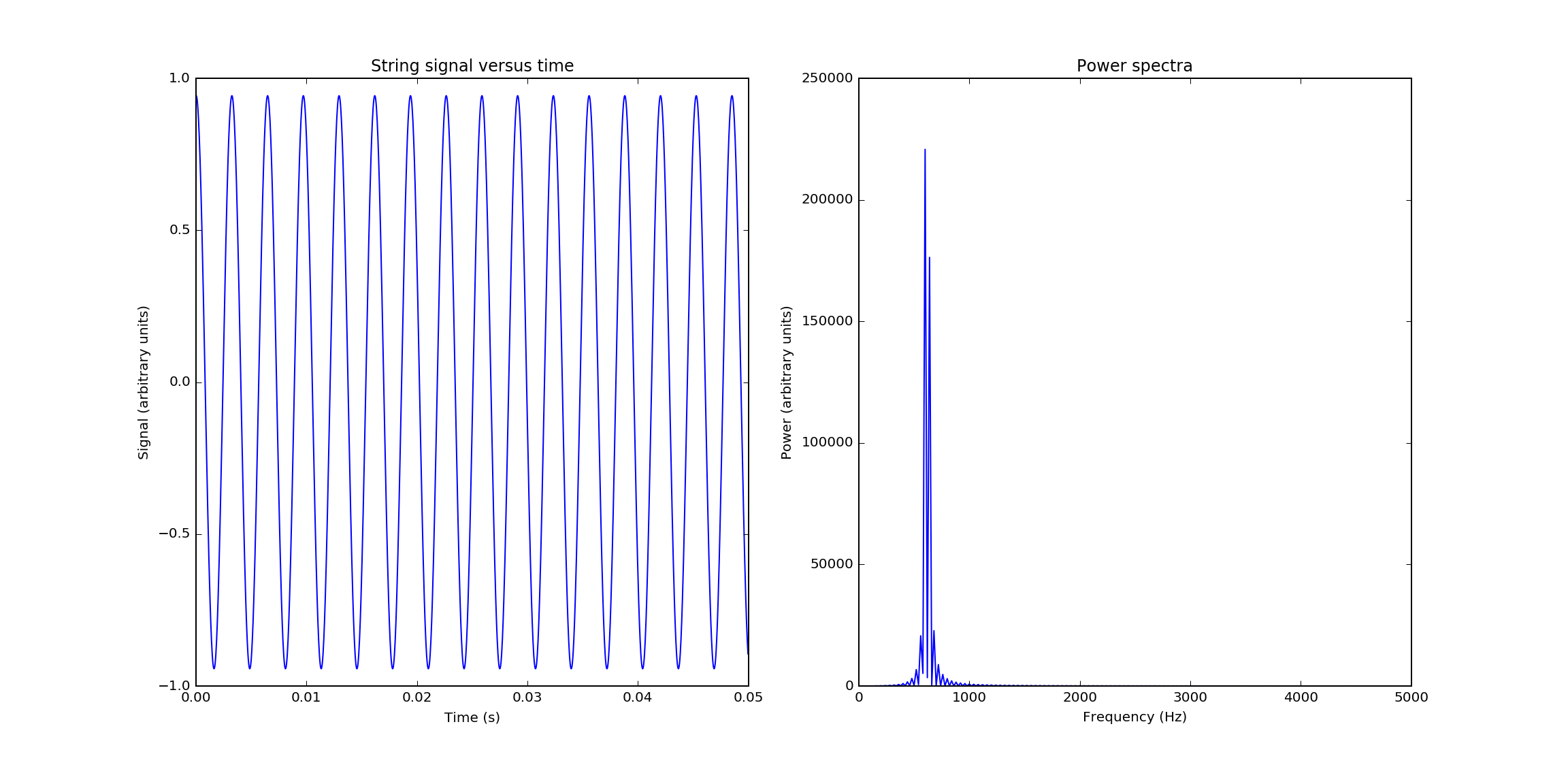
some results obtained with code1 is showed
!
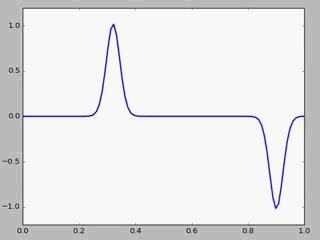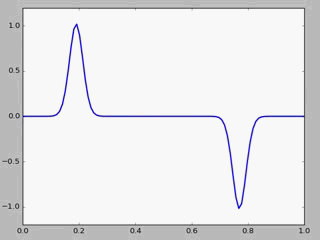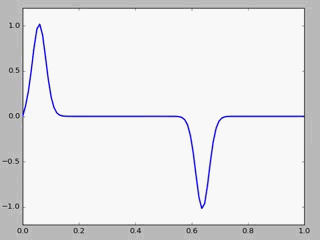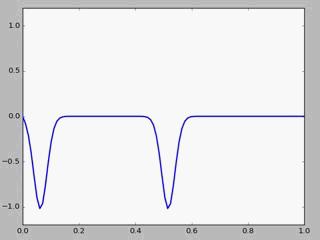Here we have assumed a simple "Gaussian pluck" pf string.That is ,we have taken the initial string profile to be

$y_0(x)=exp[-k(x-x_o)^2]$

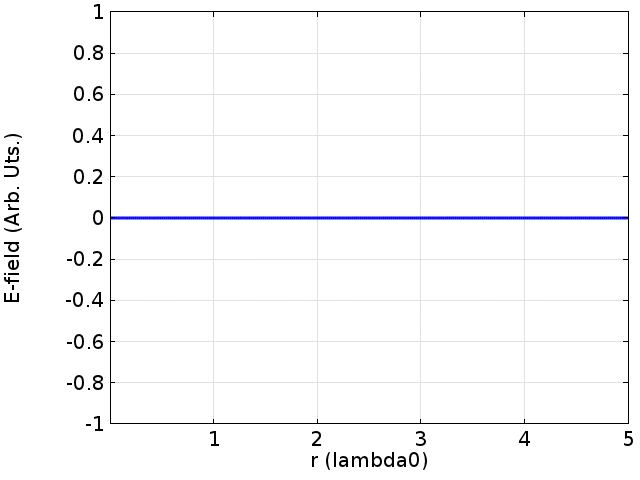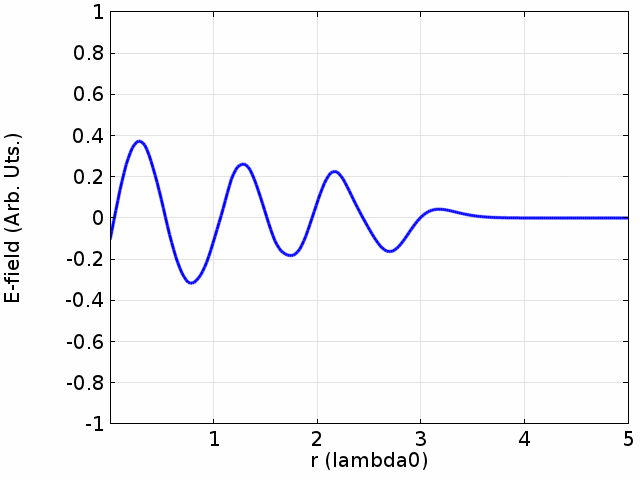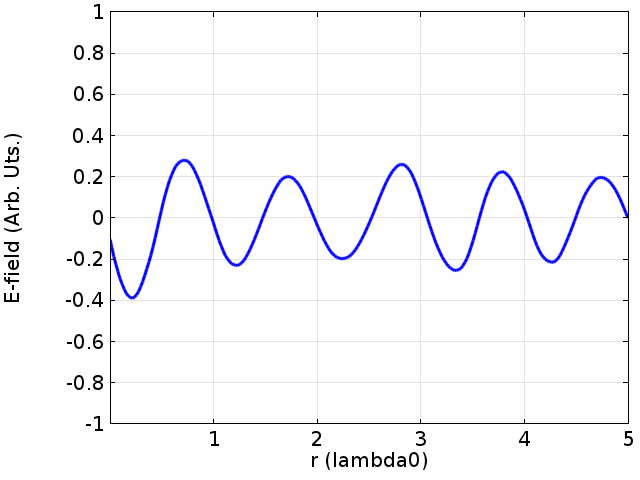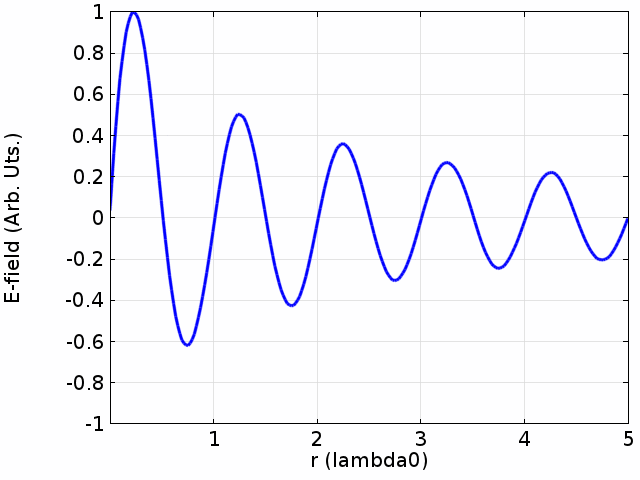
we can also give a turbulence at the left while the right is still to see how the wave transport.

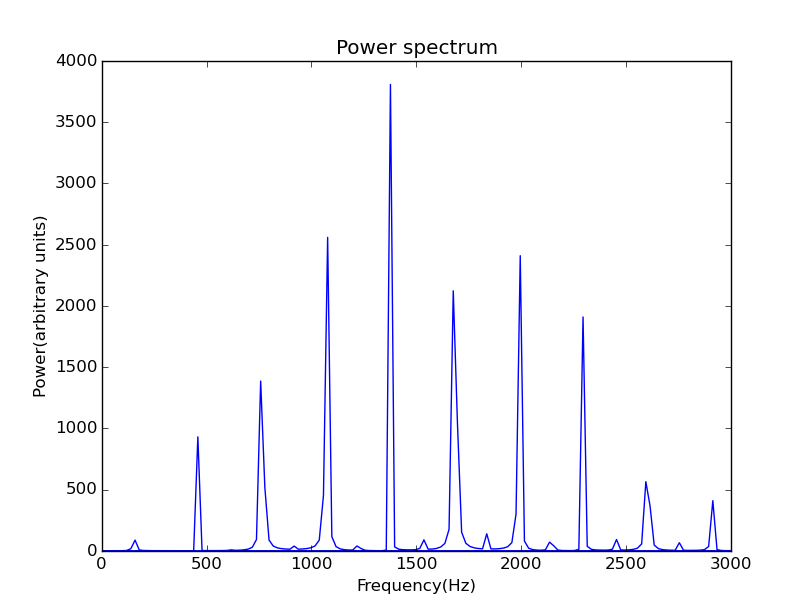
frequency spectrum of waves on a string.

Firstly,let's turn to the Fourier transform
Any function y(t) can be written as a sum of sine waves.It is convenient to express y(t) as an intergral over frequency f which is usually written in the form

$y(t)=\int_{-\propto}^{\propto}Y(f)e^{-2\pi ift}df$
while in one direction its inverse
$Y(f)=\int_{-\propto}^{\propto}y(t)e^{2\pi ift}dt$

These peaks can in terms of the standing waves that are found for a string with fixed ends.The standing waves with the longest wavelength has a wavelength $\lambda_1=2L$,the other standing waves have wavelengths of L, 2L/3.These standing waves can be thought of as the basic spatial Fourier components of the strin motion

code2

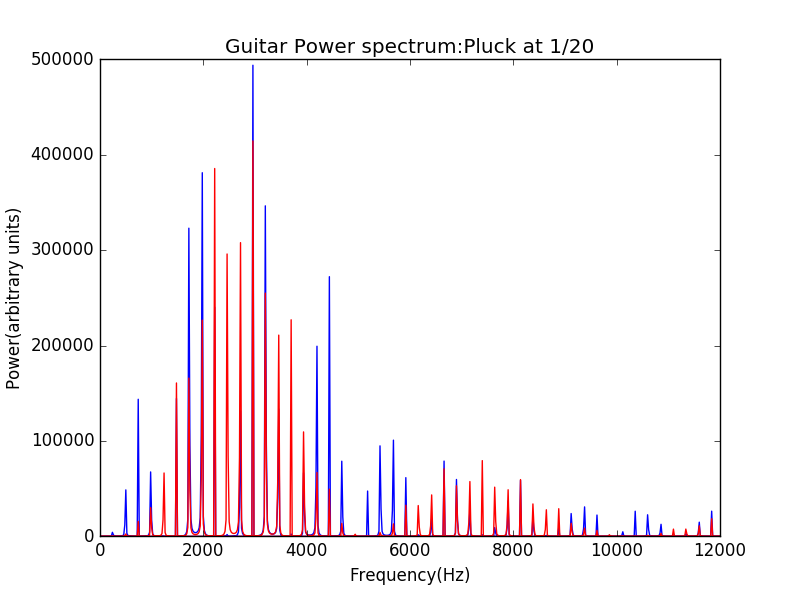
Power Spectral Density (PSD) is a frequency-domain plot of power per Hz vs frequency.

Averaging the periodograms of segments of long-duration signals more accurately assigns the power to the correct frequencies and averages to reduce noise-induced fluctuations in the power amplitudes. The tradeoff is that the frequency resolution is reduced because fewer data points are available for each FFT calculation.

The accuracy of the PSD is also improved by spectral windowing (each segment is windowed), but the windowing eliminates the contribution of the signal near the end of segment. The solution is to overlap the segments：

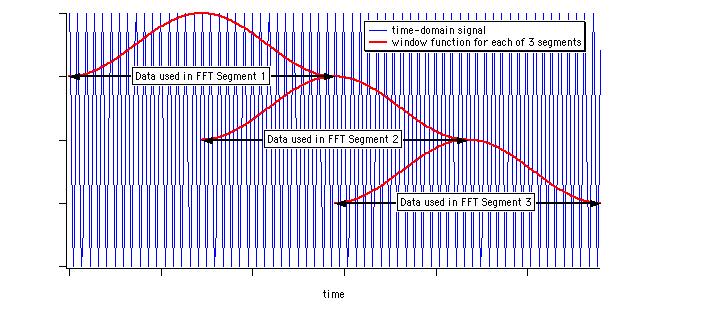
Here's an example of the averaging 8 periodograms from overlapping segments of a sampled sound:

code3

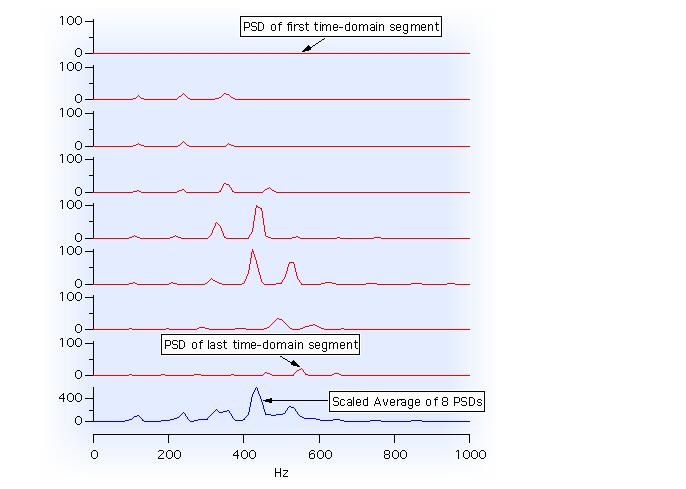
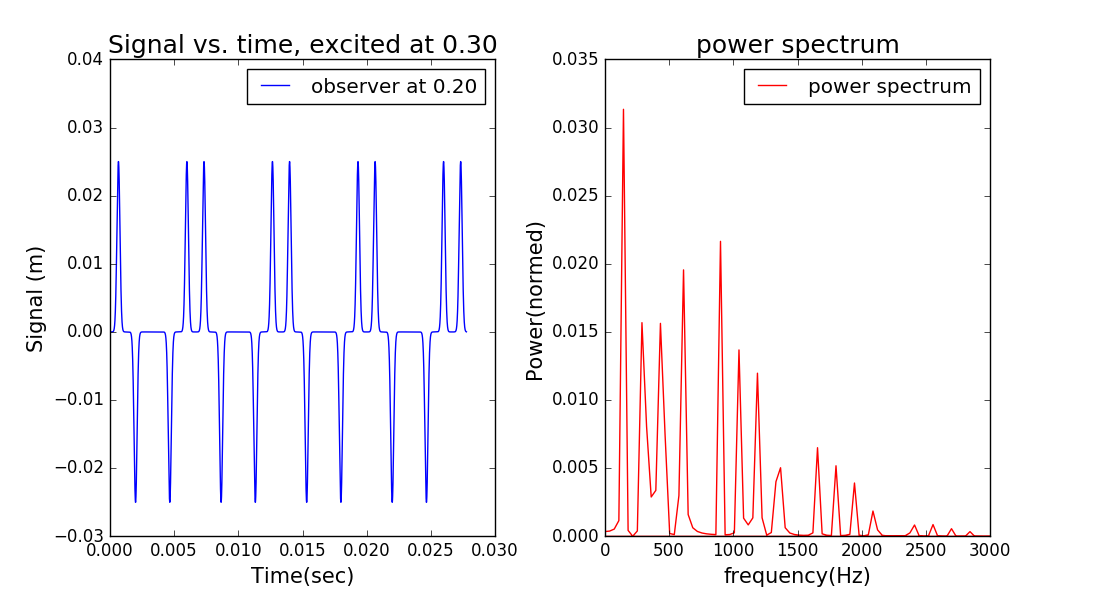
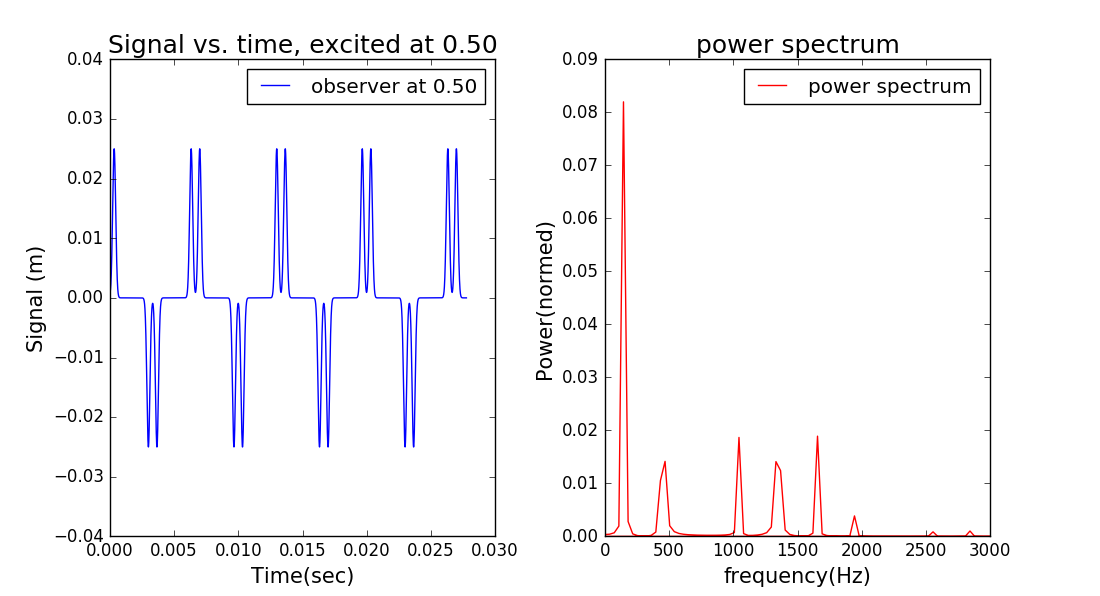
In fact,for our ideal string the magnitudes of these components do not change with time,so once we have deterimed the Fourier components for the initial wavepacket,we also have them for all laier times.If the wavepacket is located at the center of the string and is thus symmetric with respect to the center of the string.This symmetry will be preserved in the Fourier components.That is,the only Fourier components with significant amplitudes will be those that are nonzero at the center of the string and are symmetric about the center. If we give the initial disturbance at different places ,the pectrums will have different symmetry.

Thanks

Chengfeng,cheng yaoyang'code
Wikipedia
computational physics；Nicholas J. Giordano, Hisao Nakanishi.