Precise striking problem

Introduction

Generalize the program developed for the trajectory of our cannon shell including both air drag and the reduced air density under adiabatic approximation with different firing angles.The target is higher or lower than the cannon.We can also investigate how the minimum firing velocity required to hit the target varies.

Text

The first problem is how to use a constant velocity to hit target at different height.We can still use V=700m/s to test. The principle mentality is to use Euler method.
$\begin{cases}\frac{d^2x}{dt^2}=0\\\frac{d^2y}{dt^2}=-g\end{cases}$
If we add other forces like drog force,then
$\begin{cases}\frac{d^2x}{dt^2}=f_x(x,y,v_x,v_y;t)\\\frac{d^2y}{dt^2}=-g+f_y(x,y,v_x,v_y;t)\end{cases}$
$\Rightarrow$
$\begin{cases}\frac{dx}{dt}=v_x\\\frac{dv_x}{dt}=F_drag(v_x/v)\\\frac{dy}{dt}=v_y\\\frac{dv_y}{dt}=-g+F_drag(v_y/v)\end{cases}$
We can use the method of scattering the angle to find the most suitable point which is closest to the target.The smaller the angle is changed each time,the better the result is.
The folowing is the code.

import math     # import packages
import pylab as pl
import numpy as np
# class PROJECTILE solves for projectile motion with air resistance
# where : 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt: gravity acceleration and compute step size
class PROJECTILE(object):
    def __init__(self,_x0,_y0,_v0,_theta0,_B_m,_a,_alpha,_T0,_g,_dt):
        self.x= [float(_x0)]
        self.y= [float(_y0)]
        self.vx= _v0*math.cos(_theta0)
        self.vy= _v0*math.sin(_theta0)
        self.v0, self.theta0= _v0, _theta0
        self.v= _v0
        self.B= float(_B_m)        
        self.a, self.alpha, self.T0= float(_a), float(_alpha), float(_T0)
        self.g=_g
        self.dt= float(_dt)
    def calculate(self):
        while True :
            if self.y[-1]<-1E-4 :
                self.yi= self.y[-1]+self.vy*self.dt
                self.xi= self.x[-1]+self.vx*self.dt
                self.gama= -self.y[-1]/self.yi
                self.x.append((self.x[-1]+self.gama*self.xi)/(self.gama+1.))
                self.y.append(0.)
                break
            self.x.append(self.vx*self.dt+self.x[-1])
            self.y.append(self.vy*self.dt+self.y[-1])
            self.vx= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vx*self.v*self.dt+self.vx
            self.vy= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vy*self.v*self.dt+self.vy-self.g*self.dt
            self.v= math.sqrt(self.vx**2+self.vy**2)
    def store_max(self,x,v,theta):       # store the max range and theta and v0
        x.append(self.x[-1])
        v.append(self.v0)
        theta.append(self.theta0)
    def plot(self):                # plot the trace of the projectile 
        pl.plot(self.x,self.y,'--')
        pl.annotate(r'$\theta$'+'=  '+'%.2f'%(self.theta0*180./np.pi)+r'$^{o}$',
            xy=(7000,18000),fontsize=18)
        pl.annotate(r'$v_{0}$'+'=  '+'%.2f'%self.v0+r'm/s',xy=(7000,16000),fontsize=18)
        pl.annotate('start y= %.2f m'%self.y[0],xy=(7000,14000),fontsize=18)
        # class TARGET give the minimun seperation of a given orbit
# where : 
#             x_target, y_target : the target's coordinates             
class TARGET(PROJECTILE):
    def reinit(self,_x_target,_y_target):
        self.x_target= _x_target
        self.y_target= _y_target
    def deviation(self):
        self.devi= np.sqrt((np.array(self.x)-self.x_target)**2+(np.array(self.y)-self.y_target)**2)
        self.devi= [min(self.devi),self.v0,self.theta0,self.x[0],self.y[0],\
                            self.x_target,self.y_target]
        return self.devi
# class TARGET_PLUS re-solves for the orbit of a given initial state and target 
#            it will stop once it attack the target
# where : 
#             x_target, y_target : the target's coordinates
class TARGET_PLUS(PROJECTILE):
    def reinit(self,_x_target,_y_target,_len):
        self.x_target= _x_target
        self.y_target= _y_target
        self.len= _len
    def calculate(self):
        while True :
            if math.sqrt((self.x[-1]-self.x_target)**2+(self.y[-1]-self.y_target)**2)<2*self.len \
                            or self.y[-1]<-1E-4 :                
                break
            self.x.append(self.vx*self.dt+self.x[-1])
            self.y.append(self.vy*self.dt+self.y[-1])
            self.vx= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vx*self.v*self.dt+self.vx
            self.vy= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vy*self.v*self.dt+self.vy-self.g*self.dt
            self.v= math.sqrt(self.vx**2+self.vy**2)
def findextreme(to_find) :    # to find the maximum and minimum of a table
    maxvalue, maxposition= 0, 0
    minvalue, minposition= 10**9, 0
    for i in range(len(to_find)):
        if to_find[i]>maxvalue:
            maxvalue= to_find[i]
            maxposition= i
        if to_find[i]<minvalue:
            minvalue= to_find[i]
            minposition= i
    return minposition
# class PROPER_ANGEL give the proper initial angle to attack the target 
#                    initial velocity should be given
# where : 
#             x_target, y_target : the target's coordinates 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt, eps: gravity acceleration, compute step size, compute tolerant error              
class PROPER_ANGLE(object):
    def __init__(self,_up,_low,_n,_v0,_eps):
        self.up= _up
        self.low= _low
        self.n= float(_n)
        self.v0= _v0
        self.minlen= []
        self.theta= []
        self.eps =float(_eps)
    def calculate(self,_x0,_y0,_v0,_B_m,_a,_alpha,_T0,_g,_dt,_x_target,_y_target) :
        j = 1
        while True:                  # use iteration to give the angle that will attack the target
            print ('loop j=  ',j)
            self.set_range= np.linspace(self.low, self.up, self.n)            
            for i in range(len(self.set_range)):
                self.comp= TARGET(_x0,_y0,_v0,self.set_range[i],_B_m,_a,_alpha,_T0,_g,_dt)
                self.comp.calculate()
                self.comp.reinit(_x_target,_y_target)
                self.devi= self.comp.deviation()
                self.minlen.append(self.devi[0])
                self.theta.append(self.devi[2])
            self.minposi= findextreme(self.minlen)
            if (abs(max(self.minlen)-min(self.minlen))< self.eps and min(self.minlen)<10.*eps) \
                            or (j>=15):                  # once it is near enough to the target, loop will be stop
                break
            self.up, self.low= self.set_range[self.minposi]+(self.up-self.set_range[self.minposi])/5, \
                self.set_range[self.minposi]-(self.set_range[self.minposi]-self.low)/5
            j = j+1
            self.minlen, self.theta=[], []
        return self.minlen[self.minposi],self.theta[self.minposi],max(self.minlen)-min(self.minlen)
# initialize var. & para.
# where : 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt, eps: gravity acceleration, compute step size, computational tolerant error
#             xtar, ytar: target's coordinates
x0, y0= 0., [1000,2000,5000]
v0= 700.
B_m, a, alpha, T0, g= 4E-5, 6.5E-3, 2.5, 25.+273.5, 9.8
dt= 0.5
up, low= np.pi*44/90, np.pi/90
n= 30
eps= 0.1
xtar= [10000,10000,10000]
ytar= [5000,5000,5000]
# give the figure with different initialization : 
#              velocity:  fixed
#              connon's height, target's position: variable
figure= pl.figure(figsize=(15,5))
pl.subplot(1,3,1)
pl.ylabel('y  (m)',fontsize=18)
for i in range(3):
    minlen,v,theta=0,v0,0
    pro = PROPER_ANGLE(up, low, n, v0, eps)
    minlen,theta,delta= pro.calculate(x0,y0[i],v0,B_m,a,alpha,T0,g,dt,xtar[i],ytar[i])
    print( minlen,'m   ',theta*180/np.pi,'degree   ',delta,'m ')
    pro= TARGET_PLUS(x0,y0[i],v,theta,B_m,a,alpha,T0,g,dt)
    pro.reinit(xtar[i],ytar[i],minlen)
    pro.calculate()
    pl.subplot(1,3,i+1)
    pro.plot()
    pl.annotate(r'target',xy=(xtar[i],ytar[i]),xytext=(+5, +15),
         textcoords='offset points',fontsize=25)
    pl.scatter([xtar[i]],[ytar[i]],100,color= 'red')
    pl.xlim(0,32000)
    pl.ylim(0,23000)
    pl.xlabel('x  (m)',fontsize=18)
pl.show(figure)

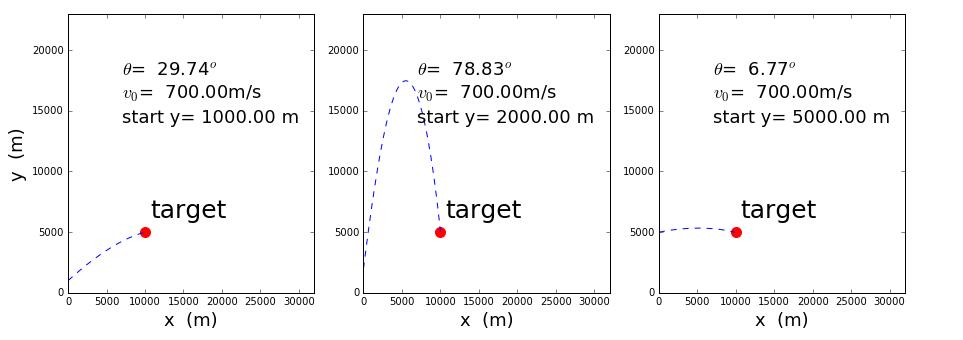
起始点分别在y轴1000米、2000米、5000米，打击点在（10000 5000）的三条曲线
We can also let the target is lower than the firing point.

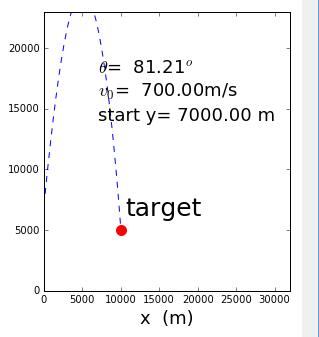
(The target is 2000m below the firing point)
Now we tend to find the smallest velocity.
As we know,the target is changed by x-coordinate and y-coordinate.Correspondingly,we should scatter the angle and the velocity to let cannon shell hit the target.

import math     # import packages
import pylab as pl
import numpy as np
# class PROJECTILE solves for projectile motion with air resistance
# where : 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt: gravity acceleration and compute step size
class PROJECTILE(object):
    def __init__(self,_x0,_y0,_v0,_theta0,_B_m,_a,_alpha,_T0,_g,_dt):
        self.x= [float(_x0)]
        self.y= [float(_y0)]
        self.vx= _v0*math.cos(_theta0)
        self.vy= _v0*math.sin(_theta0)
        self.v0, self.theta0= _v0, _theta0
        self.v= _v0
        self.B= float(_B_m)        
        self.a, self.alpha, self.T0= float(_a), float(_alpha), float(_T0)
        self.g=_g
        self.dt= float(_dt)
    def calculate(self):
        while True :
            if self.y[-1]<-1E-4 :
                self.yi= self.y[-1]+self.vy*self.dt
                self.xi= self.x[-1]+self.vx*self.dt
                self.gama= -self.y[-1]/self.yi
                self.x.append((self.x[-1]+self.gama*self.xi)/(self.gama+1.))
                self.y.append(0.)
                break
            self.x.append(self.vx*self.dt+self.x[-1])
            self.y.append(self.vy*self.dt+self.y[-1])
            self.vx= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vx*self.v*self.dt+self.vx
            self.vy= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vy*self.v*self.dt+self.vy-self.g*self.dt
            self.v= math.sqrt(self.vx**2+self.vy**2)
    def store_max(self,x,v,theta):       # store the max range and theta and v0
        x.append(self.x[-1])
        v.append(self.v0)
        theta.append(self.theta0)
    def plot(self):                 # plot the trace of the projectile 
        pl.plot(self.x,self.y,'--')
        pl.annotate(r'$\theta$'+'=  '+'%.2f'%(self.theta0*180./np.pi)+r'$^{o}$',
            xy=(5000,18000),fontsize=15)
        pl.annotate(r'$v_{0}$'+'=  '+'%.2f'%self.v0+r'm/s',xy=(5000,16000),fontsize=15)
        pl.annotate('with radii error 40m',xy=(5000,14000),fontsize=15)
# class TARGET give the minimun seperation of a given orbit
# where : 
#             x_target, y_target : the target's coordinates     
class TARGET(PROJECTILE):
    def reinit(self,_x_target,_y_target):
        self.x_target= _x_target
        self.y_target= _y_target
    def deviation(self):
        self.devi= np.sqrt((np.array(self.x)-self.x_target)**2+(np.array(self.y)-self.y_target)**2)
        self.devi= [min(self.devi),self.v0,self.theta0,self.x[0],self.y[0],\
                            self.x_target,self.y_target]
        return self.devi
# class TARGET_PLUS re-solves for the orbit of a given initial state and target 
#            it will stop once it attack the target
# where : 
#             x_target, y_target : the target's coordinates
class TARGET_PLUS(PROJECTILE):
    def reinit(self,_x_target,_y_target,_len):
        self.x_target= _x_target
        self.y_target= _y_target
        self.len= _len
    def calculate(self):
        while True :
            if math.sqrt((self.x[-1]-self.x_target)**2+(self.y[-1]-self.y_target)**2)<2*self.len \
                            or self.y[-1]<-1E-4 :                
                break
            self.x.append(self.vx*self.dt+self.x[-1])
            self.y.append(self.vy*self.dt+self.y[-1])
            self.vx= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vx*self.v*self.dt+self.vx
            self.vy= -self.B*((1-self.a*self.y[-2]/self.T0)**self.alpha)\
                           *self.vy*self.v*self.dt+self.vy-self.g*self.dt
            self.v= math.sqrt(self.vx**2+self.vy**2)
def findextreme(to_find) :          # to find the maximum and minimum of a table
    maxvalue, maxposition= 0, 0
    minvalue, minposition= 10**9, 0
    for i in range(len(to_find)):
        if to_find[i]>maxvalue:
            maxvalue= to_find[i]
            maxposition= i
        if to_find[i]<minvalue:
            minvalue= to_find[i]
            minposition= i
    return minposition
# class PROPER_ANGEL give the proper initial angle to attack the target 
#                    initial velocity should be given
# where : 
#             x_target, y_target : the target's coordinates 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt, eps: gravity acceleration, compute step size, compute tolerant error    
class PROPER_ANGLE(object):         
    def __init__(self,_up,_low,_n,_v0,_eps):
        self.up= _up
        self.low= _low
        self.n= float(_n)
        self.v0= _v0
        self.minlen= []
        self.theta= []
        self.eps =float(_eps)
    def calculate(self,_x0,_y0,_v0,_B_m,_a,_alpha,_T0,_g,_dt,_x_target,_y_target) :
        j = 1
        while True:                 # use iteration to give the angle that will attack the target
            self.set_range= np.linspace(self.low, self.up, self.n)            
            for i in range(len(self.set_range)):
                self.comp= TARGET(_x0,_y0,_v0,self.set_range[i],_B_m,_a,_alpha,_T0,_g,_dt)
                self.comp.calculate()
                self.comp.reinit(_x_target,_y_target)
                self.devi= self.comp.deviation()
                self.minlen.append(self.devi[0])
                self.theta.append(self.devi[2])
            self.minposi= findextreme(self.minlen)
            if (abs(max(self.minlen)-min(self.minlen))< self.eps and min(self.minlen)<10.*eps) \
                            or (j>=15):                   # once it is near enough to the target, loop will be stop
                break
            self.up, self.low= self.set_range[self.minposi]+(self.up-self.set_range[self.minposi])/5, \
                self.set_range[self.minposi]-(self.set_range[self.minposi]-self.low)/5
            j = j+1
            self.minlen, self.theta=[], []
        return self.minlen[self.minposi],self.theta[self.minposi],max(self.minlen)-min(self.minlen)
# initialize var. & para.
# where : 
#             x0, y0 : the connon's coordinates
#             v0, theta0 : shell's initial velocity and angle
#             B_m, a, alpha, T0 : coefficient of air resistance
#             g, dt, eps: gravity acceleration, compute step size, computational tolerant error
#             xtar, ytar: target's coordinates
x0, y0= 0., 1.
v0= 100.
B_m, a, alpha, T0, g= 4E-5, 6.5E-3, 2.5, 25.+273.5, 9.8
dt= 0.5
up, low= np.pi*44/90, np.pi/90
n= 30
eps= 0.1
xtar= 20000
ytar= 5000
# give the figure that plot the shell to attack the target
figure= pl.figure(figsize=(7,5))
pl.ylabel('y  (m)',fontsize=15)
pl.xlabel('x  (m)',fontsize=15)
pl.xlim(0,30000)
pl.ylim(0,20000)
minlen_t= []
v_t= []
theta_t= []
for i in range(0,1000,10):
    minlen,v,theta=0,v0+i*1.,0
    print( 'v =  ','%.2f'%v)
    pro = PROPER_ANGLE(up, low, n, v, eps)
    minlen,theta,delta= pro.calculate(x0,y0,v,B_m,a,alpha,T0,g,dt,xtar,ytar)
    minlen_t.append(minlen)
    v_t.append(v)
    theta_t.append(theta)
minlen = 10**9
v = 10**9
theta=0
for i in range(len(v_t)):
    if minlen_t[i]<40 and v_t[i]<v :
        minlen, v, theta= minlen_t[i], v_t[i], theta_t[i]
print ('v=  %.2f'%v,'    theta=   %.2f  degree'%(theta*180/np.pi))
pro= TARGET_PLUS(x0,y0,v,theta,B_m,a,alpha,T0,g,dt)
pro.reinit(xtar,ytar,minlen)
pro.calculate()
pro.plot()
pl.scatter([xtar],[ytar],50)
pl.annotate(r'target',xy=(xtar,ytar),xytext=(+5, +15),
         textcoords='offset points',fontsize=15)  
pl.show(figure)

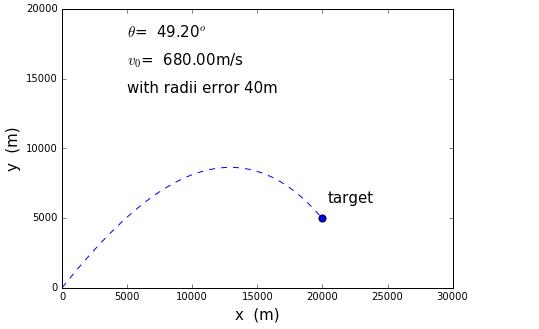
　the initial angle and velocity associated with the position of target
Input different initial place of target,we can get different angles to meet the need of minimum firing velocity.
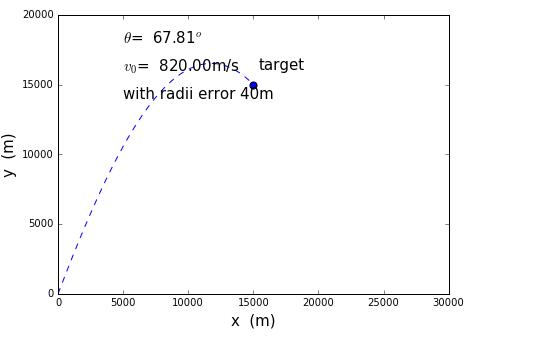
　　　　　　　　　the target is at(15000,15000)

Further discussion

add the head-on resistance.
This problem is changed into a systerm with different initial velocity along the x-coordinate.Different velocity may have a different result.

Conclusion

We can use this method to solve the practical problems about projectile problem.

Thanks

Cheng Yy's code with my debug and his suggestion.