Chaos pendulum

pendulum angle-difference driving-force Poincare-section

Abstration

Chaos is a natural but complex phenomenon around the world.Around 100 years ago,French physicist Poincaré found that the Determinism of Newtonian Mechanics was not clear when investigating three-body problem.That means the initial condition will lead to a uncertain result which means chaos.The famous example is The Butterfly Effect.

Text

Now that we have a numerical method that is suitable for various versions of the simple pendulum problem, and armed with some understanding of what might happen, an external driving force and nonlinearity.In general, we have the equation of motion
$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)$
$\rightarrow$
$\begin{cases}\frac{d\omega}{dt}=-\frac{g}{l}sin\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)\\\frac{d\theta}{dt}=\omega\end{cases}$

Firstly,we use Euler method to figure out the problem.We set initial condition same except driving force$F_D$

import math
import pylab as pl
class harmonic:
    def __init__(self, w_0 = 0, theta_0=0.2, time_constant = 1, time_of_duration = 20, time_step = 0.04,g=9.8,length=1,q=1,F=5,D=2):
        # unit of time is second
        self.n_uranium_A = [w_0]
        self.n_uranium_B = [theta_0]
        self.t = [0]
        self.g=g
        self.length=length
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        self.q=q
        self.F=F
        self.D=D
    def calculate(self):
        for i in range(self.nsteps):
            tmpA = self.n_uranium_A[i] -((self.g/self.length)*math.sin(self.n_uranium_B[i])+1*self.n_uranium_A[i]-self.F*math.sin(self.D*self.t[i]))*self.dt
            tmpB = self.n_uranium_B[i] + self.n_uranium_A[i]*self.dt
            self.n_uranium_A.append(tmpA)
            self.n_uranium_B.append(tmpB)
            self.t.append(self.t[i] + self.dt)
    def show_results(self):
        pl.plot(self.t, self.n_uranium_B,label=' F=5')
        pl.xlabel('time ($s$)')
        pl.ylabel('angle(radians)')
        pl.legend(loc='best',frameon = True)
        pl.grid(True)
a = harmonic()
a.calculate()
a.show_results()
class diff_check(harmonic):
    def show_results2(self,style='b'):
        pl.plot(self.t, self.n_uranium_B,style,label=' F=10')
        pl.xlabel('time ($s$)')
        pl.ylabel('angle(radians)')
        pl.legend(loc='best',frameon = True)
        pl.grid(True)
b=diff_check(w_0 = 0, theta_0=0.2, time_constant = 1, time_of_duration = 20, time_step = 0.04,g=9.8,length=1,q=1,F=10,D=2)
b.calculate()
b.show_results2('r')

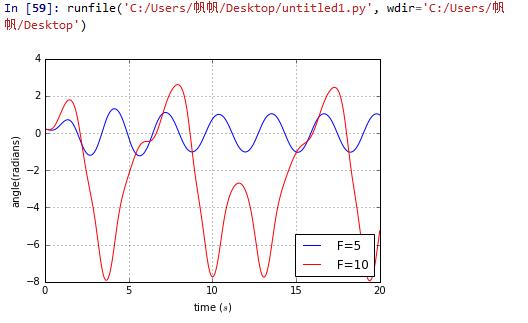
chapter3.12、3.13

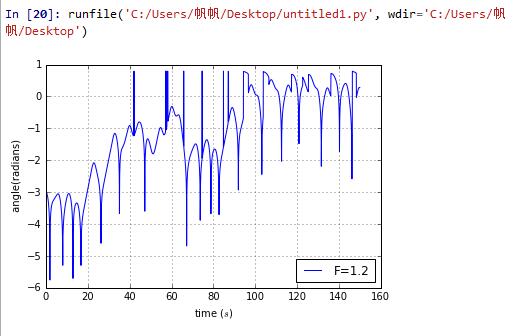
problem3.13 ask us to find $\Delta\theta\equiv|\theta_1-\theta_2|$ with time under the force
$F_{D1}=0.5 　　　F_{D2}=1.2$

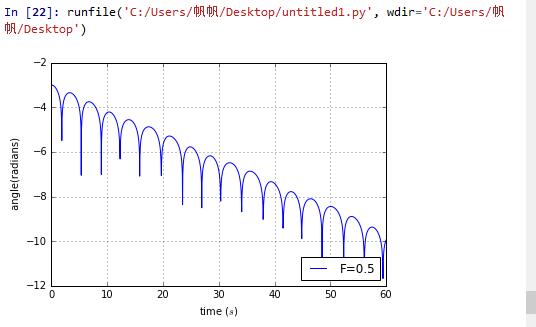
import math
import pylab as pl
class harmonic:
    def __init__(self, w_0 = 0, theta_01=0.2,theta_02=0.2+0.001, time_of_duration = 400, time_step = 0.04,g=9.8,length=9.8,q=1/2,F=1.2,D=2/3):
        # unit of time is second
        self.n_uranium_A1 = [w_0]
        self.n_uranium_B1= [theta_01]
        self.n_uranium_A2 = [w_0]
        self.n_uranium_B2= [theta_02]
        self.a=[math.log(abs(theta_02-theta_01))]
        self.t = [0]
        self.g=g
        self.length=length
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        self.q=q
        self.F=F
        self.D=D
    def calculate(self):
        for i in range(self.nsteps):
            self.n_uranium_A1.append(self.n_uranium_A1[i] -((self.g/self.length)*math.sin(self.n_uranium_B1[i])+self.q*self.n_uranium_A1[i]-self.F*math.sin(self.D*self.t[i]))*self.dt)
            self.n_uranium_B1.append(self.n_uranium_B1[i] + self.n_uranium_A1[i+1]*self.dt)
            if self.n_uranium_B1[i+1]<-math.pi:
                self.n_uranium_B1[i+1]=self.n_uranium_B1[i+1]+2*math.pi
            if self.n_uranium_B1[i+1]>math.pi:
                self.n_uranium_B1[i+1]=self.n_uranium_B1[i+1]-2*math.pi
            else:
                pass
            self.n_uranium_A2.append(self.n_uranium_A2[i] -((self.g/self.length)*math.sin(self.n_uranium_B2[i])+self.q*self.n_uranium_A2[i]-self.F*math.sin(self.D*self.t[i]))*self.dt)
            self.n_uranium_B2.append(self.n_uranium_B2[i] + self.n_uranium_A2[i+1]*self.dt)
            if self.n_uranium_B2[i+1]<-math.pi:
                self.n_uranium_B2[i+1]=self.n_uranium_B2[i+1]+2*math.pi
            if self.n_uranium_B2[i+1]>math.pi:
                self.n_uranium_B2[i+1]=self.n_uranium_B2[i+1]-2*math.pi
            else:
                pass
            self.t.append(self.t[i] + self.dt)
            self.a.append(math.log(abs(self.n_uranium_B2[i+1]-self.n_uranium_B1[i+1])))
    def show_results(self):
        pl.plot(self.t, self.a)
        pl.xlabel('time ($s$)')
        pl.ylabel(' angle(radians)')
        pl.legend(loc='upper right',frameon = True)
        pl.grid(True)
        pl.show()
a = harmonic()
a.calculate()
a.show_results()

change the force to 0.5

we can say$|\Delta\theta|=e^{\lambda t}$
$ln|\Delta\theta|=\lambda t$
for $F_{D1}=0.5$,pick two top points like(13.7903,-4.52358) and (39.3145,-7.32757) to calculate $\lambda=-0.1098/log_{10}e=0.2528$

for $F_{D1}=1.2$,pick two top points like(14.5161,-3.33464) and (60.3226,-0.362945) to calculate $\lambda=0.0649/log_{10}e=0.1494$

Poincare section

we plot $\omega$ 　versus　$\theta$ only at times that are in phase with driving force,that is,dispaly the point when $\Omega_Dt=2n\pi$

import math
import pylab as pl
class harmonic:
    def __init__(self, w_0 = 0, theta_0=0.2, time_of_duration = 10000, time_step = 0.04,g=9.8,length=9.8,q=1/2,F=1.2,D=2/3):
        # unit of time is second
        self.n_uranium_A = [w_0]
        self.n_uranium_B = [theta_0]
        self.t = [0]
        self.g=g
        self.length=length
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        self.q=q
        self.F=F
        self.D=D
        self.n_uranium_A2=[0]
        self.n_uranium_B2=[0]
    def calculate(self):
        for i in range(self.nsteps):
            self.n_uranium_A.append(self.n_uranium_A[i] -((self.g/self.length)*math.sin(self.n_uranium_B[i])+self.q*self.n_uranium_A[i]-self.F*math.sin(self.D*self.t[i]))*self.dt)
            self.n_uranium_B.append(self.n_uranium_B[i] + self.n_uranium_A[i+1]*self.dt)
            if self.n_uranium_B[i+1]<-math.pi:
                self.n_uranium_B[i+1]=self.n_uranium_B[i+1]+2*math.pi
            if self.n_uranium_B[i+1]>math.pi:
                self.n_uranium_B[i+1]=self.n_uranium_B[i+1]-2*math.pi
            else:
                pass
            self.t.append(self.t[i] + self.dt)
        for i in range(self.nsteps):
            if self.t[i]%(2*math.pi/self.D)<0.02:
                self.n_uranium_A2.append(self.n_uranium_A[i])
                self.n_uranium_B2.append(self.n_uranium_B[i])
    def show_results(self):
        pl.plot( self.n_uranium_B2,self.n_uranium_A2,'.')
        pl.xlabel('angle(radians)')
        pl.ylabel(' angle velocity')
        pl.legend(loc='upper right',frameon = True)
        pl.grid(True)
        pl.show()
a = harmonic()
a.calculate()
a.show_results()

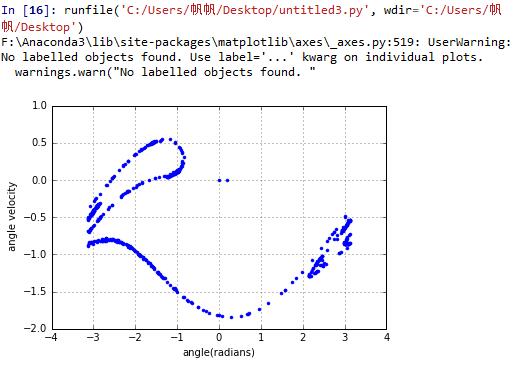
problem 3.12 ask us to change phase by $\pi/4$

so,I change the condition as followings

 if (self.t[i]-math.pi/4)%(2*math.pi/self.D)<0.02:

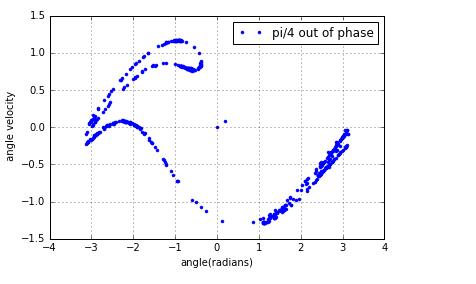
we can see two figures are apparent with a little difference.

the overall figure rises compared with figure3.9 in the textbook.

Thanks

the people who discuss this problem with me