@dongxi
2017-12-07T13:47:34.000000Z
字数 3416
阅读 1227
奇异值分解
数理统计 CS231n 降维
奇异值分解
假设说我们有一个矩阵
同时,我们有一个点,通过矩阵将转换成空间中的另一个点:
很显然,我们可以发现其几何意义就是在x轴方向拉伸为原来的3倍,而y轴方向不变的简单线性变换,也就是我们经常可以看到的对角矩阵能够产生水平/垂直方向的发射/拉伸作用。
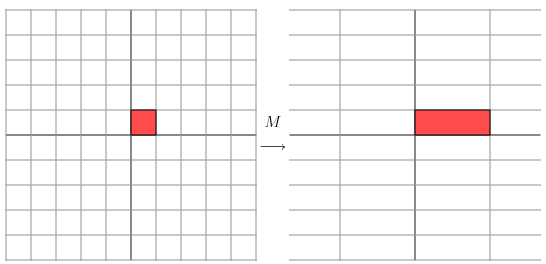
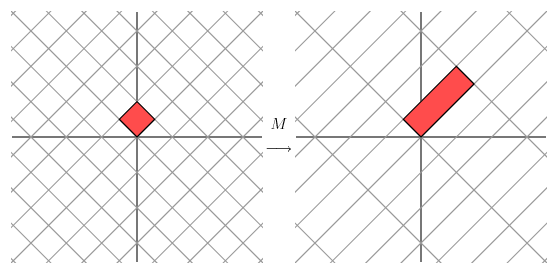
如果我们采用一个全新的矩阵,它并不是对角矩阵,是相对来说更具有一般性的对称矩阵:
那么,我们仍然可以找到一组网格线,使整个过程仅仅表现为反射/拉伸的变换,而不具有旋转变换。
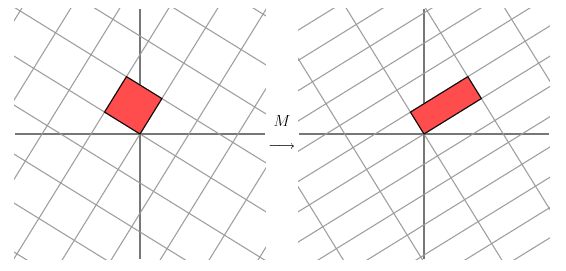
但是如果将矩阵替换为任意矩阵:
在这时,我们无论如何都不能找到一组坐标系使整个变换过程不发生旋转变换,但是还是可以保证整个过程仍然做到网格之间的相互垂直。
而奇异值就是为了完成这一过程而诞生的,它的几何意义就是对于任意一个矩阵,找到一组两两正交的单位向量序列,使得经过这一矩阵的转换以后产生的新的向量序列仍然保持两两正交。而奇异值就是指产生新的向量序列的长度。
实际上,矩阵应该就是新的向量序列与原本的正交序列之间的雅各比矩阵。
假设矩阵作用于正交单位向量和上之后,得到的和仍然满足正交条件,如下图所示:
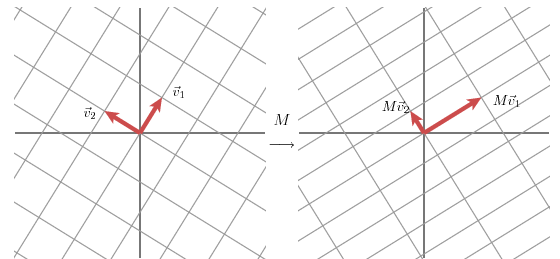
同时用和表示对应方向的单位向量,则会有:
整理以后就可以发现:
这样就得到了矩阵的奇异值分解过程,其中分别表示的长度。
除此之外,奇异值分解还有另外一种解释方法:
假设矩阵的奇异值分解为:
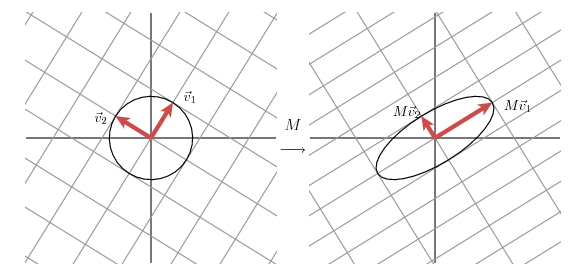
那么对于二维平面上的任意向量都可以表示为:,当作用于向量时,
令,那么如果在一个单位圆上,那么就在一个半长轴为椭圆上。这表明:矩阵将二维平面的一个单位圆变成了椭圆,同时两个奇异值就是两个半长轴长度。推广到多维空间,也是与之类似的。
奇异值分解的公式如下:
其中,是一个的矩阵,是一个的正交矩阵,又称为左奇异向量,则是的对角矩阵,同样也是一个正交矩阵,又称左奇异向量。其中,对角上的元素即奇异值。
奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小是呈正相关的。每一个矩阵都可以表示为一系列秩为1的“小矩阵”之和,而奇异值则衡量了这些“小矩阵”对于的权重。
应用
奇异值的应用也十分广泛,可以用于噪音消除、数据分析、数据压缩等方面,具体可以参考参考条目二。这里我们主要以图片的压缩为例,进行一些简单的理解。我们使用bing的壁纸来做一个简单的实验,以下是这张图片的原图:

通过奇异值分解,我们可以得到这个图片具有个奇异值,我们从中挑选一定数量的奇异值压缩图片,我们从10个奇异值开始:

实际上,只有10个奇异值,也就是全部奇异值的我们就可以看到图片的大致轮廓了,而在50个奇异值的情况下,我们已经可以较清晰的认识到整个图片的样子:

最后,我们选择108个奇异值,也就是全部奇异值的,其实跟原图已经没有很大差别了:

而对于108个奇异值的情况,我们只需要保存个参数,而对于原图我们总共需要保存个参数,压缩以后参数数目减小为了原来的,由此可见压缩效果还是很可观的。
代码如下:
import numpy as npfrom PIL import Imagedef rebuild_img(u, sigma, v, num):u_len = len(u)v_len = len(v)temp = np.zeros((u_len, v_len))for k in np.arange(num):uk = u[:, k].reshape(u_len, 1)vk = v[k].reshape(1, v_len)temp += sigma[k] * np.dot(uk, vk)temp[temp < 0] = 0temp[temp > 255] = 255return np.rint(temp).astype('uint8')if __name__ == '__main__':img = Image.open('test-2.jpg', 'r')temp = np.array(img)u_a, sigma_a, v_a = np.linalg.svd(temp[:, :, 0])u_g, sigma_g, v_g = np.linalg.svd(temp[:, :, 1])u_b, sigma_b, v_b = np.linalg.svd(temp[:, :, 2])print(len(sigma_a))print(len(u_a))print(len(v_a))for num in np.arange(10, 100, 10):R = rebuild_img(u_a, sigma_a, v_a, num)G = rebuild_img(u_g, sigma_g, v_g, num)B = rebuild_img(u_b, sigma_b, v_b, num)new_img = np.stack((R, G, B), 2)Image.fromarray(new_img).save('SVD-IMG\\test_' + str(num) + '.jpg')
