拉格朗日对偶性

数理统计 0未完成

---

前言

       本文主要是对机器学习领域中比较常见的一个数学工具拉格朗日对偶性进行简单的介绍与证明。

原始问题

       拉格朗日对偶性是一种寻找多元函数在其自变量受到一个或者多个条件约束时的极值的方法。这种方法可以将一个有$n$个变量和$m$个约束条件的最优化问题转换为一个解有$n + k$个变量的方程组问题。
       首先，定义一下我们的原问题：假设$f(x), c_i(x),h_j(x)$是定义在$R^n$上的连续可微函数，有如下具有约束的最优化问题：

$$\min f(x) \\ s.t. c_i(x) \le 0, i = 1, 2, ..., k \\ h_j(x) = 0, j = 1, 2, ..., l$$
       那么我们就可以将上式称为约束最优化问题的原始问题。我们可以和明显的得到其定义域（$dom$表示对其取定义域）：
$$\mathcal{D} = \bigcap_{i = 1}^{k}domf_i \cap \bigcap_{j = 1}^{l}domh_j$$
       对于这个原始问题我们并不是可以通过简单的求导得到其最优值，在中学时代对于这种问题，一般都是采用线性规划的方式进行求解，在这里我们会以纯代数的方式来解决这一问题。

拉格朗日函数

       对于上述问题，我们可以引入广义拉格朗日函数：

$$L(x, \alpha, \beta) = f(x) + \sum_{i = 1}^{k}\alpha_i c_i(x) + \sum_{j = 1}^{l}\beta_j h_j(x)$$
       经过上述转换，我们的定义域变为$\mathcal{D} \times R^k \times R^l$，其中$\alpha_i$和$\beta_j$被称为拉格朗日乘子，特别要求$\alpha_i \ge 0$。
       现在我们可以将$L(x, \alpha, \beta)$看做是关于$\alpha_i$和$\beta_j$的函数，需要求解其最大值，即：
$$\theta_P(x) = \max_{\alpha, \beta: \alpha_i \ge 0}L(x, \alpha, \beta)$$
       那么，我们如何将两者联系到一起？下面通过$x$是否满足约束条件两方面分析上述函数$\theta_P$。
       考虑某个$x$违反了原始的约束，即$c_i(x)>0$或者$h_j(x) \neq 0$，那么存在$\alpha_i$和$\beta_j$满足下式：
$$\theta_P(x) = \max_{\alpha, \beta: \alpha_i \ge 0}\left[f(x) + \sum_{i=1}^k\alpha_i c_i(x) + \sum_{j = 1}^{l}\beta_j h(_jx) \right] = + \infty$$
       如果$c_i(x)>0$，我们可以去$\alpha_i \rightarrow +\infty$即可，同理当$h_j(x) \neq 0$时，只需$\beta_j \rightarrow +\infty$。
       考虑$x$满足原始的约束，那么：
$$\theta_P(x) = \max_{\alpha, \beta: \alpha_i \ge 0}\left[f(x) \right] = f(x)$$
       当我们选择合适的$\alpha_i$和$\beta_j$时，我们就可以很容易的得到$\theta_P(x)$的便是其本身$f(x)$。
       我们可以对上述内容进行简单的归纳，可以得出：
$$\theta_P(x) = \left\{ \begin{aligned} f(x), \ x满足原始问题约束 \\ + \infty, \ x不满足原始问题约束 \end{aligned} \right.$$

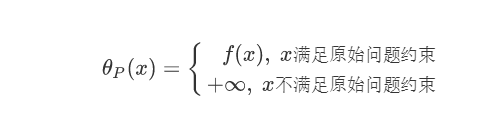
       那么，在满足约束的条件下，我们有：
$$\min_x\theta_P(x) = \min_x \max_{\alpha, \beta: \alpha_i \ge 0}L(x, \alpha, \beta) = \min_x f(x)$$
       所以，我们$\min_x\theta_P(x)$与原优化问题等价，所以经常会使用$\min_x\theta_P(x)$代表原始问题，为了方便接下来的表述，我们用$p^*$表示原始问题的最优值，即：
$$p^* = \min_x\theta_P(x)$$

对偶问题

       接下来到了我们的重点部分，有些时候原始问题的形式，我们难以求解，我们可以对这些问题进行对称化。
       定义关于$\alpha$和$\beta$的函数：

$$\theta_D(\alpha, \beta) = \min_x L(x, \alpha, \beta)$$
       这里需要注意到一点，在本定义中，等式右侧是关于$x$的函数最小化，最小值是一个关于$\alpha$和$\beta$的函数。
       我们对$\theta_D(x)$求最大化，那么会有：
$$\max_{\alpha, \beta: \alpha_i \ge 0} \theta_D(\alpha,beta) = \max_{\alpha, \beta: \alpha_i \ge 0} \min_x L(x, \alpha, \beta)$$
       我们将这个问题定义为原始问题的对偶问题，我们将原始问题写出来：
$$\min_x \theta_P(x) = \min_x \max_{\alpha, \beta: \alpha_i \ge 0}L(x, \alpha, \beta) = \min_x L(x, \alpha, \beta)$$
       两者在形式上极其相似，只是交换了$\min$和$\max$的相对位置，将原问题转变成了先固定$\alpha$和$\beta$，优化$x$，然后在确定参数$\alpha$和$\beta$。
       与上文相似，为了方便表示我们定义：
$$d^* = \max_{\alpha, \beta: \alpha_i \ge 0} \theta_D(\alpha,beta)$$

对偶问题与原始问题的关系

       原始问题和对偶问题并不是一定相等的，他们的关系有如下定理：
定理：若原始问题与对偶问题都有最优值，则：

$$d^* = \max_{\alpha, \beta: \alpha_i \ge 0} \min_x L(x, \alpha, \beta) \\ \le \min_x \max_{\alpha, \beta: \alpha_i \ge 0}L(x, \alpha, \beta) =\ p^*$$
       对于上述定理其实是可以很容易想到的，但是“拍脑门”不是我们的目的，其证明如下：

对于任意的$\alpha$、$\beta$和$x$，我们有：

$$\theta_D(\alpha, \beta) = \min_x L(x, \alpha, \beta) \le L(x, \alpha, \beta) \\ \le \max_{\alpha, \beta: \alpha_i \ge 0}L(x, \alpha, \beta) = \theta_P(x)$$
即：
$$\theta_D(\alpha, \beta) \le \theta_P(x)$$
由于原始问题与对偶问题都有最优值，那么会有：
$$\max_{\alpha, \beta: \alpha_i \ge 0} \theta_D(\alpha,beta) \le \min_x \theta_P(x)$$
即：
$$d^* = \max_{\alpha, \beta: \alpha_i \ge 0} \theta_D(\alpha,beta) \\ \le \min_x \theta_P(x) = p^*$$

       那么，原始问题的最优解不小于对偶问题的最优解，这是一个很有用的结论，但并不是我们想得到的。如果我们希望使用对偶问题去求解原始问题，那么就必须要求对偶问题的最优值和原始问题最优值相等才可以，那么在什么条件下才能使$d^* = p^*$呢？这个条件就是所谓的$KTT$条件。

KTT条件

       当$d^* = p^*$成立时，满足的条件被称为$KTT$条件。我们来简单的推导一下$KTT$条件，首先为了方便讨论我们对约束条件进行一定的简化：

$$\min f(x) \\ s.t. h_j(x) = 0, i = 1, 2, ..., l$$
       很明显，我们的目标函数为：
$$\min{x, \beta}L(x,\beta) = f(x) + \beta_jh_j(x)$$
       根据数学知识我们可以知道，取得最小值的必要条件为：
$$\nabla_xL = \frac{\partial L}{\partial x} = \nabla_xf + \beta_j\nabla_x h_j = 0$$
$$\nabla_{\beta_j}L = \frac{\partial L}{\partial \beta_j} = h_j = 0$$
       其中第一个方程，我们成为定常方程（stationary equation），第二个则称为束缚条件。通过上面两式，我们可以很容易的得到最优值时的$x$和$\beta$的取值。
       接下来，增加一下复杂度，现在的约束条件为：
$$\min f(x) \\ s.t. c_i(x) \le 0, i = 1, 2, ..., k \\ $$
       束缚不等式$c_i(x) \le 0$成为原始可行性（primal feasibility），据此我们可以定义可行域$K = \{x \in R^n| c(x) \le 0\}$（这在前面有所提及）。假设$x^*$为满足束缚条件的最佳解，对于最佳解$x^*$存在两种情况：

1. $c(x^*) < 0$，最佳解位于$K$内部，称为内部解，这时束缚条件无效。
2. $c(x^*) = 0$，最佳解位于$K$内部，成为边界解，这使束缚条件则是有效的。

       对于这两种情况采用的解决方式是不同的，对于内部解的情况，实际上就是约束无效的情况，$c(x^*) < 0$也就不会产生效果，有约束问题退化成了无约束问题，因此$x^*$只需要满足$\nabla f = 0$且$\beta = 0$。而对于边界解时，束缚条件退化成了在之前我们提及到得模型，那么很显然会有$\nabla_xf = - \alpha_i\nabla_x c_i$，这里的$c_i \ge 0$是有意义的，以本题为例，我们希望最小化$f(x)$，而梯度$\nabla f$（函数$f$在点$x$上升最快的方向）一般指向可行域$K$内部，但是$\nabla c$却指向$K$的外部区域，所以$\beta \ge 0$，这项性质成为对偶可行性。
       同时我们可以发现无论是内部解还是边界解，都会有$\alpha_i \nabla c = 0$成立，这项性质称为补松弛。整合上述两种情况，最佳解需要的四个条件为：定常方程式、原始可行性、对偶可行性和补松弛(三个性质待补充)：

$$\nabla_xf + \alpha\nabla_x c = 0 \\ c(x) \le 0 \\ \alpha \ge 0 \\ \alpha c(x) = 0 \\ $$
       同样，如果我们要最大化$f(x)$，并且将原始可行性更改为$c(x) \le 0$，那么要将对偶可信性更改成$\beta \le 0$。
       对于多个约束的条件，我们也可以很容易得到$KTT$条件，对于：
$$\min f(x) \\ s.t. c_i(x) \le 0, i = 1, 2, ..., k \\ h_j(x) = 0, j = 1, 2, ..., l$$
       我们可以推导出$KTT$条件为：
$$\nabla_xL = 0 \\ h_j(x) = 0, j = 1, 2, ..., l \\ c_i(x) \le 0, i = 1, 2, ..., k \\ \alpha_i \ge 0, i = 1, 2, ..., k \\ \alpha_i c_i(x) = 0 , i = 1, 2, ..., k \\ $$

结语

       本篇博客基本上就算是初稿完成了，还是有很多地方说的不清不楚，不明不白的，这些部分等我看完线性代数的知识或者学习完《凸优化》再进行补充，应该也不会太晚，应该在今年之内。

参考
拉格朗日乘数
凸优化（八）——Lagrange对偶问题
简易解说拉格朗日对偶（Lagrange duality）
Karush-Kuhn-Tucker (KKT) 條件