机器学习可行性-VC维度

0完成 机器学习 机器学习基石 CS229 Learning-From-Data

---

前言

       机器学习是一种非常非常有力的工具，它能够通过一定的数据预测剩下的数据，实现一个学习的过程，但是机器学习为什么可以预测？本文借助VC维度这一概念，来粗浅的解释一下这个问题(本文章中，提及到的机器学习任务都默认是二分类问题，推广到其他问题与二分类问题相似)。

$E _{in}$和$\Omega$

       机器学习过程中，我们希望可以使用样本的统计量来估计总体的参数，所以我们必须要有一个假设，就是样本和总体服从同一分布，在我目前的认知中，这也是机器学习的最基本的条件，如果这一条件都无法满足，那么，我认为机器学习是无法进行的。所以，以下的所有问题，我们都假设样本和总体是服从同一分布的。
       对于服从同一分布的情况，样本和总体会满足一定的条件，其中Hoeffding's Inequality就描述了这种性质：

$$\mathbb{P}[|\mid \nu-\mu \mid>\epsilon]\leq 2exp(-2\epsilon ^2N)$$
       上式中，$\nu$表示样本的平均值，$\mu$表示总体的平均值，$\epsilon$表示我们的容忍度。同时，我们可以定义样本中错误概率$E _{in}$和总体中的错误概率$E _{out}$为：
$$E_{out}(h) = \underset{x\sim P}{\mathbb{E}} [h(x)\neq f(x)]$$
$$E_{in}(h) = \frac{1}{N}\sum_{n=1} ^ {N}[h(x_n)\neq y_n]$$
       那么，我们可以推导出：
$$\mathbb{P}[|E_{in}(h)-E_{out}(h)|\gt \epsilon]\leq 2 exp(-2\epsilon ^2N)$$
       所以只要右侧的上界足够小，我们就可以认为$h$在样本的表现力与总体的表现力相似，但是这并不是意味着这个$h$是一个很好地算法，很明显如果$E_{in}(h)$本身就很大，那么$h$也并不会在总体上表现的很好。现在我们就可以将我们在最开始提出的问题进行简单的转换：
$$E _{out}(h) = E _{in}(h) + \Omega$$
       只要$E _{in}$和$\Omega$都很小，那么就可以得到一个很小的$E _out$，这也是我们的目的所在。因此我们需要一个较小的$E _{in}(h)$，所以我们通过$\mathcal{A}$在$\mathcal{H}$上选择一个最好的$h$，用符号$g$表示，，只要$\mathcal{H}$足够大，我们的选择范围就越广，那么就一定可以得到一个很小的$E _in$，那么似乎我们的问题结束了，然而并不是这样。
       我们是通过$\mathcal{A}$在$\mathcal{H}$上选择合适的$h$，对于任意一个$h$，我们都有$\mathbb{P}[|E_{in}(h)-E_{out}(h)|\gt \epsilon]\leq 2 exp(-2\epsilon ^2N)$成立，这主要是由于我们在选择样本是完全随机，可能就是选出来的样本对于$h$不是很好，我们称这样的样本$\mathcal{D}$是一个$\mathcal{BAD\ D}$，这种样本实际上不会对我们的$E _{in}$产生什么影响，而在之前我们提及的$\mathcal{A}$在选择$h$时，完全以$E _{in}$为选择依据，那么只要对于任意一个$h$，样本$\mathcal{D}$为$\mathcal{BAD\ D}$就有可能导致我们最后选择的$g$的$\Omega{g}$很大，那么现在我们遇到$\mathcal{BAD\ D}$的上界则变为了（$M$表示$\mathcal{H}$中$h$的数量）：
$$\begin{aligned} \ & \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}] \\\ \ & = \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1\ or\ BAD\ \mathcal{D}\ for\ h_2\ or\ ...\ or\ BAD\ \mathcal{D}\ for\ h_M]\\\ \ & \leq \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1] + \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_2]+...+\mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_M] \\\ \ & \leq 2exp(-2\epsilon ^2N) + \leq 2exp(-2\epsilon ^2N) + ... + \leq 2exp(-2\epsilon ^2N) \\\ \ & = 2Mexp(-2\epsilon ^2N) \end{aligned}$$
       换言之，$E _{out}$是否足够小，在很大程度上与$\mathcal{H}$中的$h$数目有关，如果我们的$M$很小，那么得到$g$就很难保证$E _in$会很小，而如果$M$很大，那么就无法保证$\Omega(h)$可以保持在可以接受的范围内。

有效方程$h$

       在之前的推导中，我们使用了一个很大的上限，我们认为$H$遇到$\mathcal{BAD\ D}$等于每一个方程遇到的概率之和。这是一个很大的上界，如果方程$h _1\approx h _2 \approx h _3$，那么他们遇到$\mathcal{BAD\ D}$的事件也应该是十分相似的，如下图，如果可以将接近的方程相互合并，那么或许可以将$M$限制到一个可以接受的范围。

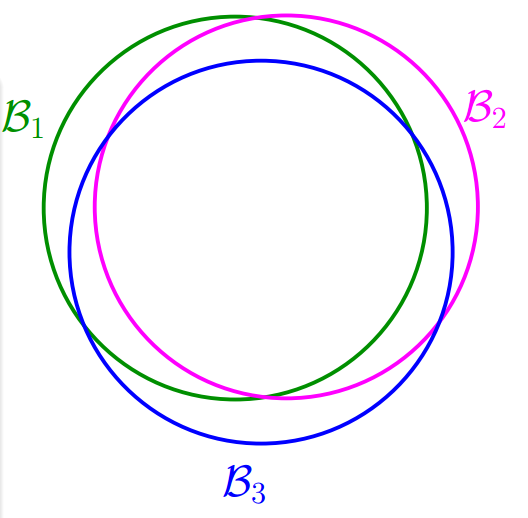
       现在假设要从平面上挑选一条直线作为$g$将一个数据$x ^{(1)}$进行分类，很显然$\mathcal{H}$中是有无数个方程的（参数范围为实数域），但是由于产生结果只有两类，所以可以将方程分为两类：

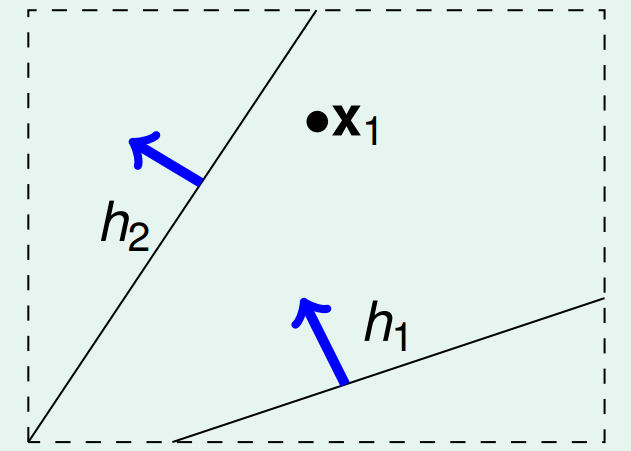
       如果我们的数据点变为两个$x ^{(1)}$和$x ^{(2)}$，那么可以产生四种结果，也就意味着有四种直线：

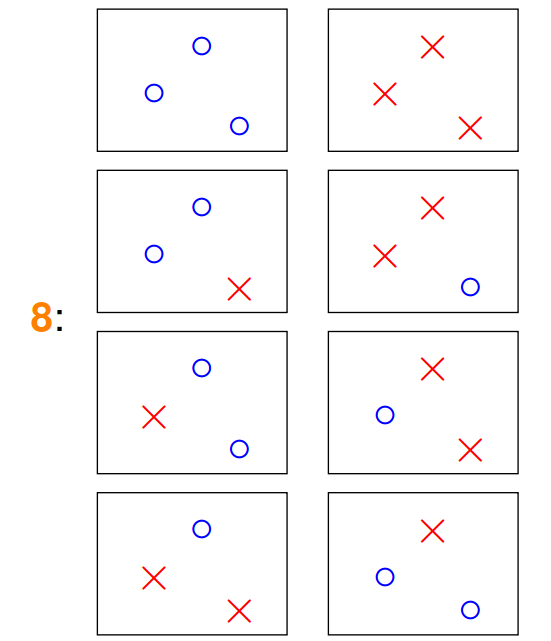
       同理，如果有三个数据点，便可以出现8种分类结果，也就是会可以产生8类直线进行分割（不考虑三点共线的情况，在这里我们只讨论最多产生的直线分类）：

       那么，对于四个数据点的情况，我们可以出现16种分类组合，但是好像可以产生的分类类型出现了一点变化：

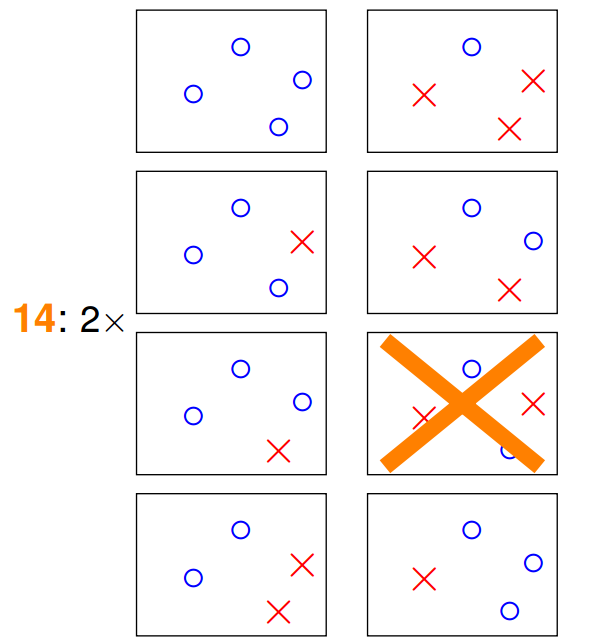
       很明显有一种情况我们是无法用线性进行分割的，对于这种情况，我们最多产生14种直线进行分割。这里我并没有找到很严格的证明，但是我们可以启发性的认为属于同一类的直线，他们将会同时遇到/不遇到$\mathcal{BAD\ D}$，所以新的上限可以进行一定程度的紧缩：

$$\mathbb{P}[|E_{in}(g)-E_{out}(g)|\gt \epsilon]\leq 2\cdot effective(N)\cdot exp(-2\epsilon^2N)$$
       通过观察上式，我们发现只要能够让$effective(N)$增加速度小于指数，比如多项式速度，那么只要我们取无限大的数据，就可以得到一个$E _{in}(g) \approx E _{out}(g)$，那么我们如何推导$effective(N)$呢？

增长函数

       在以下的过程中，我们使用一个$dichotomy$代表$\mathcal{H}$中一种类型的直线，而$Dichotomies$代表能够产生直线类型的集合，所以我们会有

$$effective(N) = num\ of\ dichotomy$$
       那么，对于一个$\mathcal{H}$最多产生多少种不同的$dichotomy$，很显然这是一个与$H$和$N$都相关的数据，我们可以用以下方式表示：
$$\max \mid \mathcal{H} (x ^{(1)}, x ^{(2)},\dots, x ^{(N)})$$
       这个式子又被成为增长函数（Growth Function）。如果我们采用确定的$\mathcal{H}$进行机器学习过程，那么增长函数很显然是一个只与$N$相关的函数。以下是几个常见的$\mathcal{H}$的成长函数：

1. Positive Rays

   
          这是一个很简单的模型，如果大于值$a$，那么我们就预测点$x ^{(n)}$为$+1$，反之则预测为$-1$，很明显，这时我们的增长函数为：$m_{\mathcal{H}(N)}=N+1$。

2. Positive Intervals

       与上述类似，使用简单的排列组合，可以推导出此时我们的成长函数为：$m_{\mathcal{H}(N)}=\binom{N+1}{2} + 1 = \frac{1}{2}N^2 + \frac{1}{2}N + 1$。
3. Convex Sets

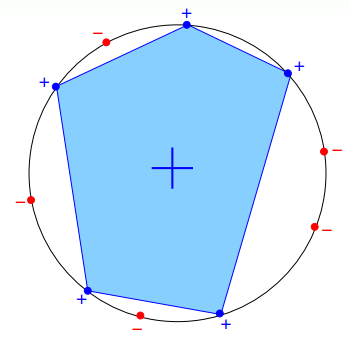
       对于一个凸集合，从中任选$k$个点，这些点包裹的空间范围，预测为$+1$，那么增长函数并不是多项式级别的，而是指数级别的，即：$m_{\mathcal{H}(N)}=2^N$。

Shatter & Break Point

       以上只是列举了少数几个特别简单的$\mathcal{H}$，那么对于一个不是那么简单的$\mathcal{H}$，比如多维空间的线性分割，我们该如何推导增长函数呢？
       首先，我们引入两个比较简单的概念，Shatter和Break Point。如果当$\mathcal{H}$作用于有$N$个样本的$\mathcal{D}$时，产生的$dichotomies$数量与$2 ^N$相等，那么我们就说这$N$个输入被$\mathcal{H}$给shatter掉了。
       对于一个给定的成长函数$m _H{N}$，从$N = 1$开始，对于第一个$k$，使当$N \ge k$时，永远有$m _H(N) \lt 2 ^k$，那么我们称$k$是成长函数$m _H{N}$的break point，也就是意味着对于任何的$N \ge k$，$\mathcal{H}$都无法shatter（其实，只要break point为k，那么任何$N \gt k$都不可能被shatter）。
       以二维平面的线性分类问题为例，当$N = 1， 2$时，总可以shatter，对于$N = 3$时，存在可以shatter的情况，但是当$N = 4$时，任何情况$\mathcal{H}$都不可以shatter，换言之，4便是该$\mathcal{H}$的break point。
       我们简单推导一下这一过程，首先假设我们有个$\mathcal{H}$的break point为2，那么对于$N = 3$时，增加一个dichotomy，那么会有：

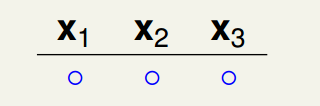
       很显然，这是可能成立的，我们继续增加dichotomy，那么：

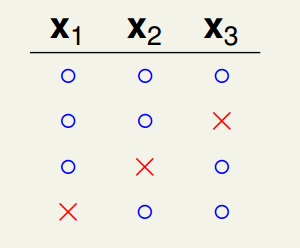
       我们再增加一个我们继续增加dichotomy：

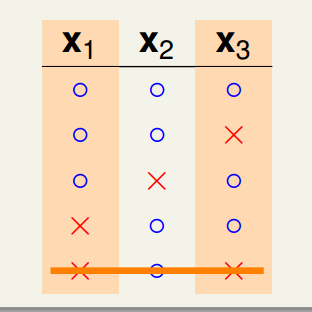
       此时，出现了不可以被shatter的内容，因为我们已经列举了$x ^{(1)}$和$x ^{(3)}$的所有情况，这与$break\ point = 2$的事实不符，继续尝试可以发现，我们已经无法增加任何组合了。因此，$N = 3, break\ point = 2$时，能够产生的dichotomies最多便是4种。
       为了方便起见，我们采用$B(N, k)$表示$break\ point = 2$的任意的$\mathcal{H}$能够产生的最大的dichotomies的数量（这里的$\mathcal{H}$是任意的，是一个很宽的上限，比如该例可能$B(2, 2) \lt 3$）。
       虽然说，一般的情况下我们都是难以得到一个准确的$m_H$，但是我们是可以推导出$m_H(N)$的上界$B(N, k)$的。我们可以很轻易的得到下表：

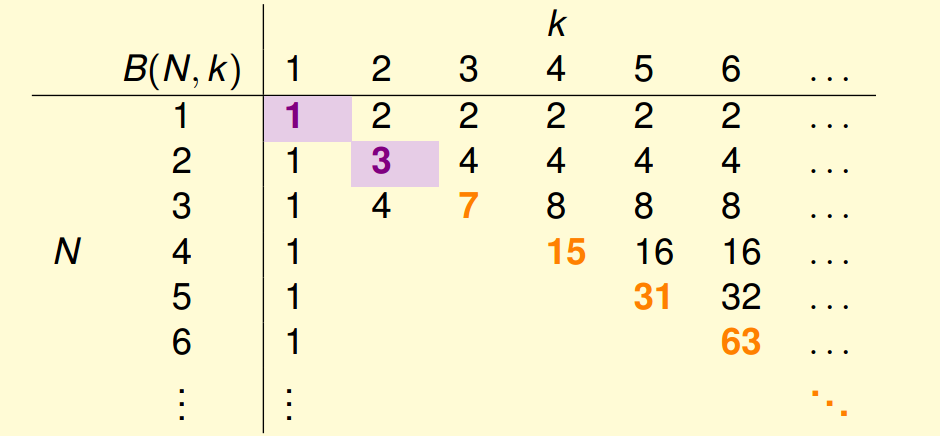
       但是，如何能够填写表格中还处于空白的部分呢？我们穷举$B(4, 3)$中所有的dichotomies穷举出来，然后进行简单的排序：

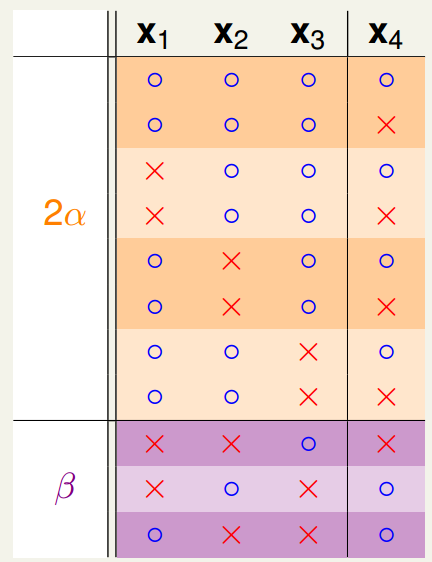
       其中，$\alpha$部分中的$x^{(1)} \sim x^{(3)}$都是成对出现的，而$\beta$则都是单独存在的。下面我们去掉$x ^{(4)}$，然后将重复的部分进行合并：

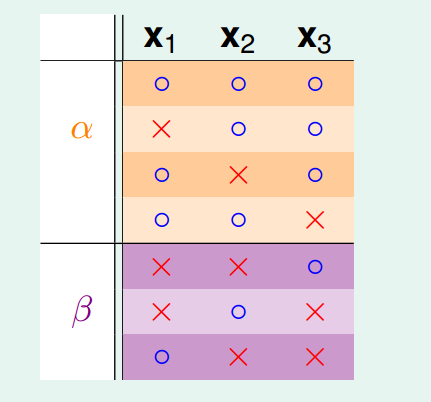
       很显然，对于$\alpha + \beta$部分一定是不能被shatter的，所以会有：$\alpha + \beta \le B(3, 3)$。接下来，单独看$\alpha$部分，则有：

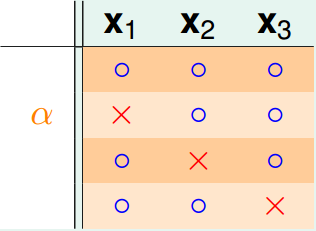
       $N = 4$的情况下，$\alpha$是成对存在的，如果在$\alpha$可以被shatter掉任何两个点，那么就可以和$x ^{(4)}$产生的dichotomies就可以被shatter了，与我们的$k = 3$不符，因此$\alpha$不能被shatter任何两个点shatter，即：$\alpha \le B(3, 2)$。
       到目前为止，我们终于可以推导出了$B(4, 3)$的上界，也就是：

$$B(4, 3) = 2\alpha + \beta \le B(3, 3) + B(3, 2) = 11$$
       同理，我们可以得到一个递推式：
$$\begin{aligned} B(N,k) &= 2\alpha + \beta \\\ \alpha + \beta &\leq B(N-1,k) \\\ \alpha &\leq B(N-1,k-1) \\\ \Rightarrow B(N,k) &\leq B(N-1,k) + B(N-1,k-1) \end{aligned}$$
       通过数学归纳法，可以我们有（$\binom{n + 1}{m} = \binom{n}{m} + \binom{n}{m - 1}$）：
$$\begin{aligned} B(N_{o}+1,k) &\leq B(N_{o},k) + B(N_{o},k-1) \\\ &\leq \sum_{i=0}^{k-1}\binom{N_{o}}{i}+\sum_{i=0}^{k-2}\binom{N_{o}}{i} \\\ &=1+\sum_{i=1}^{k-1}\binom{N_{o}}{i}+\sum_{i=1}^{k-1}\binom{N_{o}}{i-1} \\\ &=1+\sum_{i=1}^{k-1}[\binom{N_{o}}{i}+\binom{N_{o}}{i-1}] \\\ &=1+\sum_{i=1}^{k-1}\binom{N_{o}+1}{i}=\sum_{i=0}^{k-1}\binom{N_{o}+1}{i} \end{aligned}$$
       到此为止，我们已经可以将前面的空白地方填充上：

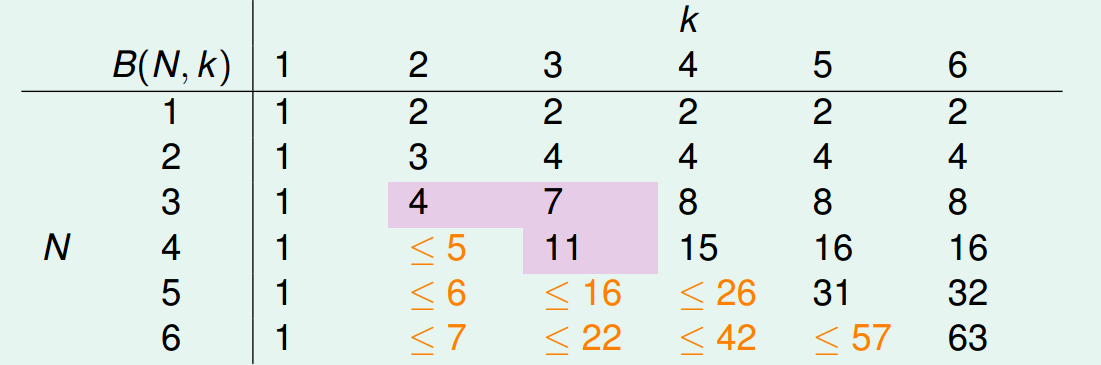
       所以，只要我们能够求出$\mathcal{H}$的break point，那么只要样本足够大，我们就可以认为机器学习产生的结果是有效的，也就是$E_{in} \sim E_{out}$。

VC维度

       在前文中，我们可以知道如果$\mathcal{H}$中存在一个break point，那么就可以保证其增长速度一定是多项式级别的，同时根据上面的推导，很显然break point越大，那么相应的$\mathcal{H}$复杂度也就会越高，在这里引入VC维度（VC Dimension）这一概念来表述$\mathcal{H}$的复杂度（实际上，直接用break point也应该是可以的描述的）。
       一个$\mathcal{H}$的VC维度（记为$d_{vc}(\mathcal{H})$）描述了其能在任何情况shatter的最多的点集中点数目，很显然，$d_{vc} + 1 = k(break\ points)$，因此增长函数的上界可以变更为：

$$m_{\mathcal{H}}(N)\leq \sum_{i=0}^{d_{vc}} \binom {N}{i} \leq N^{d_{vc}}+1$$

VC bound

       到目前为止，我们似乎已经将要证明的东西证明出来了，在确定这件事之前，我们在确定一下，现在我们有的不等式可以写成这样：

$$\mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon]\leq 2m_{\mathcal{H}}(N)\cdot exp(-2\epsilon ^2N)$$
       仔细观察下，发现好像有点不大对，我们之所以能够推导出一个$m_H$，是因为$\mathcal{H}$中点的数目有限，所以产生的$E_{in}$是有限的，才可以将$\mathcal{H}$分类，然而对于out of sample的情况，点是无穷无尽的，很显然只要$h$产生任意一点的变化，求得的$E_{out}$就会发生变化，因此对于$E_{in}$来说，$\mathcal{H}$是有限的，而对于$E_{out}$则是无限的，而这种无限可能无法更改的。那么现在我们希望能够将$E_{out}$进行简单的替换，把$E_{out}$变为有限个。
       假设我们能够在总体中再取得$N$笔资料作为验证集（Verification Set）$\mathcal{D'}$，那么对于任何一个$h$，我们都可以求出一个有限的$E_{in}'$，我们启发式的认为如果$E_{in}$的概率与$E_{out}$差距很大的话，那么$E_{in}$与$E_{in}'$也不会很相似。

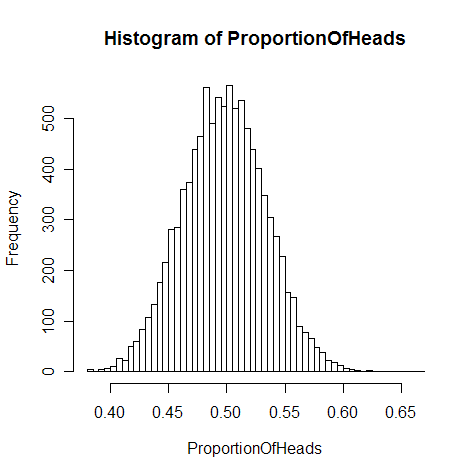
       实际上，由于中心极限定理可以知道当$N$很大的时候，$E_{in}$可以$E_{in}'$服从以$E_{out}$为中心的近似的正态分布，如上图。$[|E_{in}-E_{out}|\text{ is large}]$事件发生完全取决于$\mathcal{D}$。如果$[|E_{in}-E_{out}|\text{ is large}]$已经发生了，则如果我们从总体中在抽出一份$D'$，则会有50%左右的概率会发生$[|E_{in}-E_{in}^{'}|\text{ is large}]$，还有大概50%的概率$[|E_{in}-E_{in}^{'}|\text{ is not large}]$，实际上，最终我们可以得到如下结论（$sup$表示上确界）：
$$(1-2e^{-\frac{1}{2}\epsilon^2N})\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]\leq \mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}]$$

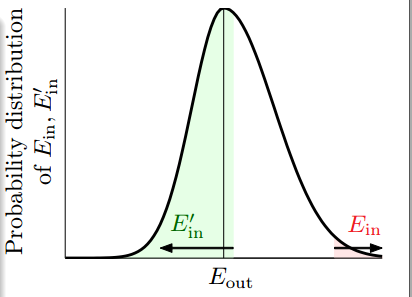
       从RHS出发，会有（主要运用了贝叶斯公式）：
$$\begin{aligned} &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &\geq \mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2} \mathbf{\;and\;} \underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &=\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \;\times \\\ &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ \end{aligned}$$
       再来看下不等式的最后一项，对于一个固定的$\mathcal{D}$来说，$h$的选择是只与$\mathcal{D}$有关，而与$\mathcal{D'}$无关的，对于一个固定的$\mathcal{D}$，任选一个$h ^*$使$|E_{in}(h^{*})-E_{out}(h^{*})|\gt \epsilon$，成立，那么上式变为：
$$\begin{aligned} &\;\;\;\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \\\ &\geq \mathbb{P}[|E_{in}(h^{*})-E_{in}^{'}(h^{*})| \gt \frac{\epsilon}{2}\;\;|\;\;\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon] \end{aligned}$$
       再引入一个比较有意思的东西：
$$\left.\begin{matrix} |E_{in}^{'}(h^*) - E_{out}(h^*)|\leq \frac{\epsilon}{2}\\\ |E_{in}(h^*)-E_{out}(h^*)| \gt \epsilon \end{matrix}\right\} \Rightarrow |E_{in}(h^*)-E_{in}^{'}(h^*)| \gt \frac{\epsilon}{2}$$
       很明显，LHS的两个式子是RHS的充分条件，而在原式中$E_{in}(h^*)-E_{out}(h^*)| \gt \epsilon$是作为条件的，那么原式又可以进一步的转换：

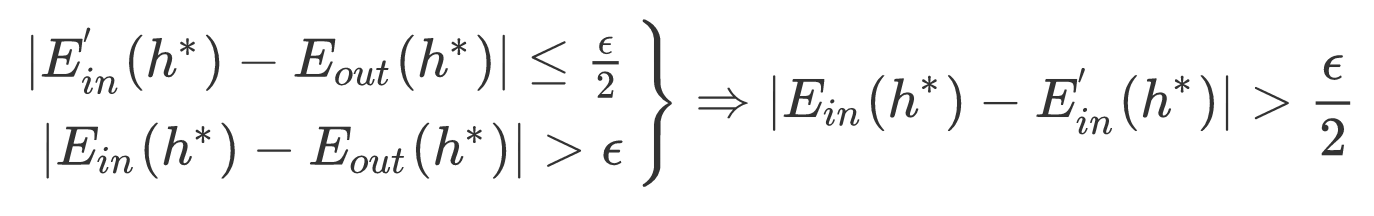
       第一个不等号就是上面叙述的内容，第二个不等号主要运用了Hoeffding Inequality，推导如下：
$$\begin{aligned} &\;\;\;\,\mathbb{P}[|...|\gt \epsilon]\leq 2Mexp(-2\epsilon^2N) \\\ &\Leftrightarrow 1-\mathbb{P}[|...|\gt \epsilon]\geq 1-2Mexp(-2\epsilon^2N) \\\ &\Leftrightarrow \mathbb{P}[|...|\leq \epsilon]\geq 1-2Mexp(-2\epsilon^2N) \end{aligned}$$
       在之前的讨论中，明确了$h ^*$的选择与$\mathcal{D'}$无关，那么很很显然$M = 1$成立，将原式带入就可以得到$\mathbb{P}[|...|\lt \frac{\epsilon}{2}]\geq 2exp(-\frac{1}{2}\epsilon^2N)$，到目前为止我们就得到了之前提及的式子，也就是：
$$(1-2e^{-\frac{1}{2}\epsilon^2N})\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]\leq \mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}]$$
       对$e^{-\frac{1}{2}e^2N}$一般可以采取一个比较合理的约束，$e^{-\frac{1}{2}e^2N} \lt \frac{1}{4}$，在此时将$1-2e^{-\frac{1}{2}e^2N}\gt \frac{1}{2}$带入上式，则会有：
$$\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{out}(h)| \gt \epsilon]\leq 2\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}]$$
       这与上面我们启发式的讨论的相似，现在我们可以认为我们一次取得了$2N$笔数据，分别为$\mathcal{D}$和$\mathcal{D'}$，而$\mathcal{H}$则变为了出现在$\mathcal{D}+\mathcal{D'}$最多能产生的dichotomies数目$m_{\mathcal{H}}(2N)$了。所以，我们新的$\mathbb{P}[BAD]$为：
$$\begin{aligned} \mathbb{P}[BAD] &\leq 2\,\mathbb{P}[\underset{h\in \mathcal{H}}{sup}\ |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &\leq 2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \end{aligned}$$
       前面的数据相当于建立一个
N的bin，然后从中抽取N个数据（不放回抽取），那么我我们需要知道新的bin中的分布，如果可以知道这个分布，那么我们就可以使用Hoeffding without replacement，将之推算出来了，而bin中的分布为$\frac{E_{in}+E_{out}}{2}$，又因为：
$$|E_{in}-E_{in}^{'}|\gt \frac{\epsilon}{2} \Leftrightarrow |E_{in} - \frac{E_{in}+E_{in}^{'}}{2}|\gt \frac{\epsilon}{4}$$
       所以原式又可以进行一定的转换：
$$\begin{aligned} \mathbb{P}[BAD] &\leq 2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-E_{in}^{'}(h)| \gt \frac{\epsilon}{2}] \\\ &=2\,m_{\mathcal{H}}(2N)\,\mathbb{P}[\text{fixed } \textit{h} \text{ s.t. } |E_{in}(h)-\frac{E_{in}(h)+E_{in}^{'}(h)}{2}| \gt \frac{\epsilon}{4}]\\\ &\;\;\;\text{(Hoeffding without replacement)} \\\ &\leq 2\,m_{\mathcal{H}}(2N)\cdot 2\,exp(-2(\frac{\epsilon}{4})^2N) \end{aligned}$$
       这个上限被称为VC bound：
$$\begin{aligned} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \end{aligned}$$
       这便是机器学习可行性的理论保障之一。总的来说，如果希望机器学习可以进行那么就要求有以下三个要求：

1. $\mathcal{H}$的$d_{vc}$有限，保障VC Bound存在。（good $\mathcal{H}$）
2. $N$相对于$d_{vc}$足够大，这样可以保证bound有意义。(good \mathcal{D})
3. 算法$\mathcal{A}$能够选择一个足够优秀的$g$，使$E_{in}$足够小。（good $\mathcal{A}$）

       对于$d_{vc}$较小的$\mathcal{H}$，我们可以比较容易的求出到什么情况完全无法在shatter了，但是对于比较复杂的模型就比较困难了，这时可以根据模型的自由度（模型中可以自由变动的参数个数，即我们的机器需要通过学习来决定的参数个数）近似的得到一个$d_{vc}$。比如我们之前的例子：

1. Positive Rays：需要确定1个参数，这个参数就是机器需要根据$\mathcal{D}$来确定的一个参数，则Positive Rays中自由的参数个数为1，即$d_{vc} = 1$；
2. Positive Intervals：需要确定左右2个参数，则可以由机器自由决定的参数的个数为2，$d_{vc} = 1$；
3. d-D Perceptrons：d维的感知机，可以由机器通过学习自由决定的参数的个数为$d + 1$， $d_{vc} = d + 1$。

模型选择

       回顾我们之前提及的两个问题：

1. $E_{in}$和$E_{out}$能否足够接近；
2. $E_{in}$能否足够小。

       这就导致了如果我们选择的$\mathcal{H}$不能过大，同样也不能过小，要合适才好，不过，合适才是最难的。令$\delta = VC\ Bound$，那么我们希望的$[|E_{in}(g)-E_{out}(g)|\leq \epsilon]$发生概率就变为了$1-\delta$，其中$1-\delta$又被称为置信度。经过简单的推导，我们可以得到$\epsilon$为：

$$\sqrt{\frac{8}{N}\ln\left(\frac{4(2N)^{d_{vc}}}{\delta}\right)} = \epsilon$$
       那么，我们可以将$E_{in}$和$E_{out}$可以表示为：
$$E_{in}(g)-\sqrt{\frac{8}{N}\ln\left(\frac{4(2N)^{d_{vc}}}{\delta}\right)} \leq E_{out}(g) \leq E_{in}(g)+\sqrt{\frac{8}{N}\ln\left(\frac{4(2N)^{d_{vc}}}{\delta}\right)}$$
       其中$\sqrt{\frac{8}{N}\ln\left(\frac{4(2N)^{d_{vc}}}{\delta}\right)}$称为模型复杂度，一般用$\Omega (N,\mathcal{H},\delta)$表示，模型复杂度用来衡量$E_{in}$和$E_{out}$的差异程度。我们可以绘制出下图：

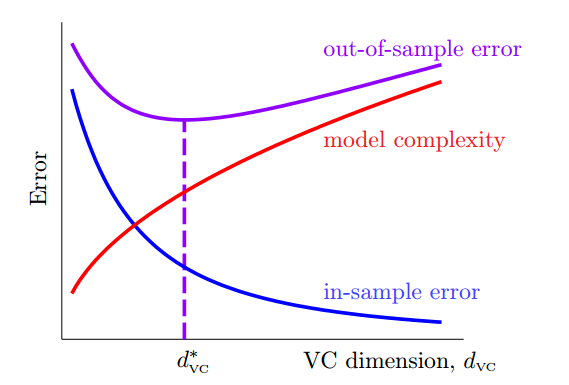
       很显然，$d_{vc}^*$是最好的情况，由此可见，合适的才是最好的。
       很显然，$\Omega (N,\mathcal{H},\delta)$随着$N$的增大而减小，理论上讲，只要有无穷无尽的数据，我们的$d_{vc}$也可以很大很大，但是我们不可能有无穷无尽的数据，所以对于一个$d_{vc}$需要多少数据量呢？一般来说，我们希望保证置信率$1-\delta =90\%$，根据VC Bound计算大致上$N\approx 10,000d_{vc}$，不过这是一个很宽松的范围，在经验上，一般来说满足$N\approx 10d_{vc}$就可以得到比较好的结果了。

总结

       本篇文章最开始是由于CS 229中关于VC维度那章节去查阅资料时，发现机器学习基石好像最初的几节课都是在讲这个东西的，就去看了机器学习基石，可是没想到前七节课都是讲的这个，然后就索性全都看了，还买了书。
       在写本篇文章时，很大程度上借鉴了机器学习笔记中的内容，其中的内容写的确实很详尽，建议阅读。

参考

Machine Learning Foundations (機器學習基石)
机器学习笔记
Learning From Data