高斯判别分析

机器学习 CS229 0未完成

---

前言

       高斯判别分析（GDA）是生成学习算法中的一种（虽然名字中有判别两字），在本模型中，我们假设$p(x|y)$符合多元正态分布，在介绍高斯判别分析之前，先简要介绍下多元正态分布。

多元正态分布

       在多元正态分布是正态分布在多维变量下的扩展，其均值$\mu \in R^n$，协方差矩阵$\Sigma \in R^{n \times n}$，与正态分布的表达式相似，多元正态分布的形式如下（$|\Sigma|$表示行列式）：

$$p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp\left(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)\right)$$
       其中，将$\Sigma$的多元正态分布称为标准正态分布，同样我们可以知道当$\Sigma$为对角矩阵，同时相应位置的值越大，那么其图像就应该越“矮胖”；相应位置的值越小，其图像就应该越“瘦小”（从方差的角度很容易理解）。

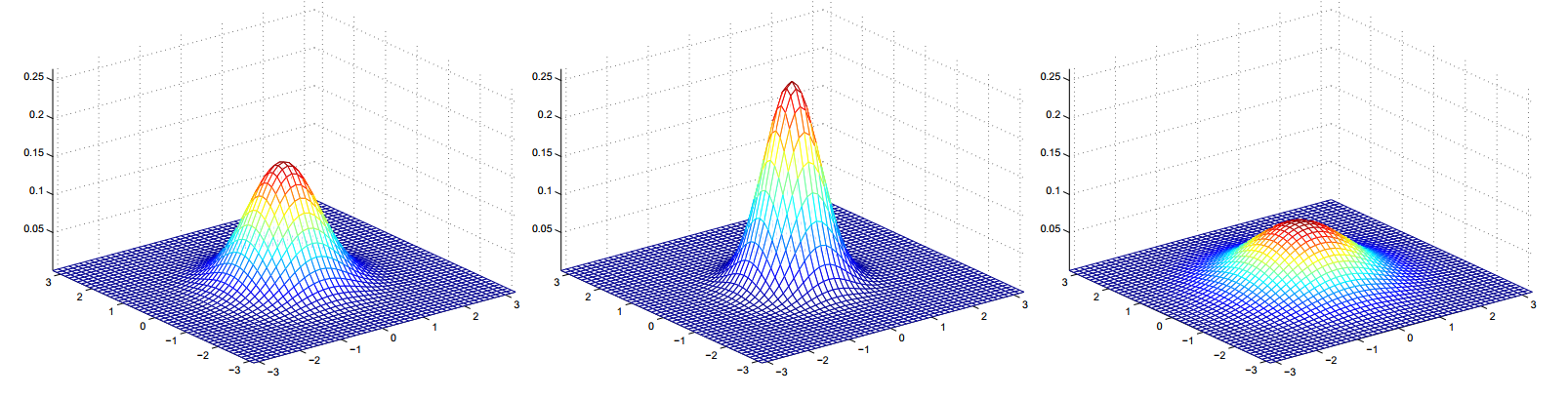
       以上三幅图的协方差矩阵如下，很显然，这与我们之前的想象是相同的。
$$\Sigma =\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} ,\Sigma =\begin{bmatrix} 0.6 & 0 \\ 0 & 0.6 \\ \end{bmatrix} ,\Sigma =\begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}$$

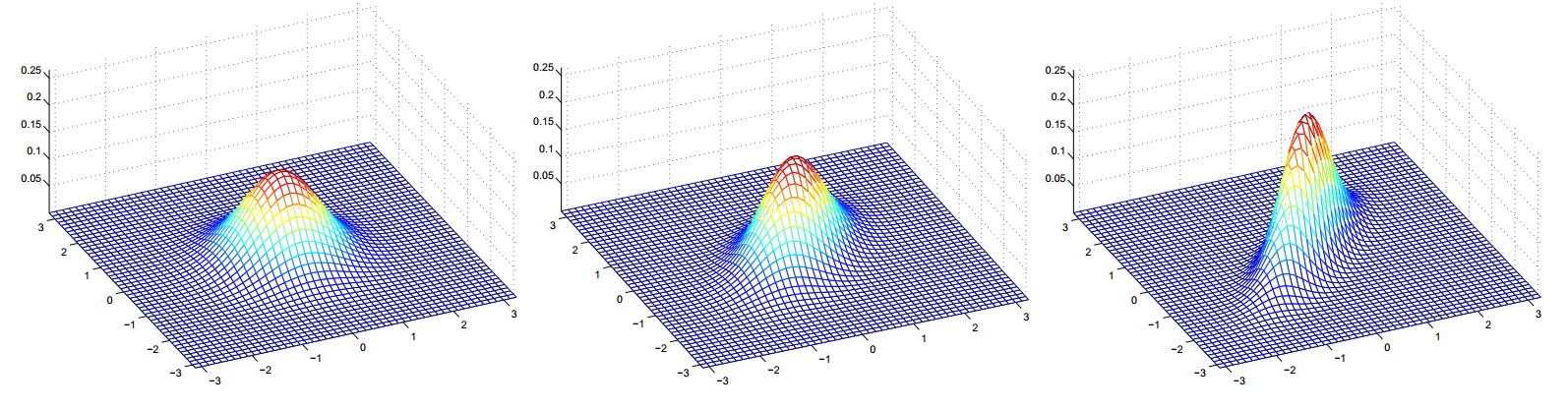
       以上三幅图则是去掉了$\Sigma$是对角矩阵的条件，对应的图像也发生了巨大的变化，它们的协方差矩阵如下，协方差越大，则表明了它们之间的相关性越强，如果协方差与两者标准差之积相等（也就是相关系数为1），那么图像就应该是条线。
$$\Sigma =\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} ,\Sigma =\begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \\ \end{bmatrix} ,\Sigma =\begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \\ \end{bmatrix}$$

高斯判别分析模型

       高斯判别分析模型适用于连续随机值的分类问题。这个模型的基本假设是目标值$y$服从伯努利分布，条件概率$p(x|y)$服从正态分布，如下：

$$y \sim Bernoulli(\phi) \\ x|y = 0 \sim N(\mu_0,\Sigma) \\ x|y = 1 \sim N(\mu_1,\Sigma)$$
       写成概率模式则是：
$$p(y) = \phi^y(1 - \phi)^{1 - y} \\ p(x|y = 0) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp\left(-\frac{1}{2}(x - \mu_0)^T\Sigma^{-1}(x - \mu_0)\right) \\ p(x|y = 1) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}exp\left(-\frac{1}{2}(x - \mu_1)^T\Sigma^{-1}(x - \mu_1)\right)$$
       虽然上述表达式中存在$\mu_0$和$\mu_1$，但一般来说它们是具有同一个协方差的，所以说对于高斯判别是模型一共有四个参数，$\phi$、$\Sigma$、$\mu_0$以及$\mu_1$。跟往常一样，我们还是采用最大似然估计来求解模型：

$$l(\phi,\mu_0,\mu_1,\Sigma) = \log \prod_{i = 1}^{m}p(x^{(i)},y^{(i)},\mu_0,\mu_1,\Sigma) \\ = \log \prod_{i = 1}^{m}p(x^{(i)}|y^{(i)},\mu_0,\mu_1,\Sigma)p(y^{(i)};\phi) \\ = \sum_{i = 1}^{m}\log p(x^{(i)}|y^{(i)},\mu_0,\mu_1,\Sigma) + \sum_{i = 1}^{m}\log p(y^{(i)};\phi) \\ = \sum_{i = 1}^{m}(1 - y^{(i)})\log p(x^{(i)}|y^{(i)} = 0) + \sum_{i = 1}^{m}y^{(i)}\log p(x^{(i)}|y^{(i)} = 1) \\ + \sum_{i = 1}^{m}\log p(y^{(i)};\phi)$$

       还是原来的方法，这里有四个参数，那我们就分别对这四个参数求偏导数，很显然我们的结论是：

$$\phi = \frac{1}{m}\sum_{i = 1}^{m}I\{y^{(i) = 1}\} \\ \mu_0 = \frac{\sum_{i = 1}^{m}I\{y^{(i)} = 0\}x^{(i)}}{\sum_{i = 1}^{m}I\{y^{(i)} = 0\}} \\ \mu_1 = \frac{\sum_{i = 1}^{m}I\{y^{(i)} = 1\}x^{(i)}}{\sum_{i = 1}^{m}I\{y^{(i)} = 1\}} \\ \Sigma = \frac{1}{m}\sum_{i = 1}{m}(x^{(i)} - \mu_y^{(i)})$$
       下面对上面这几个式子进行一下简单的推导：
$$\frac{\partial l(\phi,\mu_0,\mu_1,\Sigma)}{\partial \phi} = \frac{\partial\sum_{i = 1}^{m} \log p(y^{(i)})}{\partial \phi} \\ = \frac{\partial \sum_{i = 1}^{m}y^{(i)}\log \phi + (1 - y^{(i)})\log (1 -\phi)}{\partial \phi} \\ = \sum_{i = 1}^{m}\frac{y^{(i)}}{\phi} + \frac{1 - y^{(i)}}{1 -\phi} \\ = 0$$
      然后很显然就可以推导出上述的式子一了。
$$\frac{\partial l(\phi,\mu_0,\mu_1,\Sigma)}{\partial \mu_0} = \frac{\partial\sum_{i = 1}^{m}(1 - y^{(i)})\log p(x^{(i)}|y^{(i)} = 0)}{\partial \mu_0} \\ = \sum_{i = 1}^{m}(1 - y^{(i)})(\Sigma^{-1}(x^{^(i) - \mu_2})) \\ = 0$$
    同样根据对称性可以求得$\mu_1$的值（关于矩阵的导数还一脸懵逼，过程待补充，先抄上）。最后就是对$\Sigma$求偏导数，很显然最后一项可以忽略不计，那么先将前两项改写：
$$\sum_{i = 1}^{m}(1 - y^{(i)})\log p(x^{(i)}|y^{(i)} = 0) + \sum_{i = 1}^{m}y^{(i)}\log p(x^{(i)}|y^{(i)} = 1) \\ = \sum_{i = 1}^{m}(1 - y^{(i)})\left(\log\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}-\frac{1}{2}(x^{(i)} - \mu_0)^T\Sigma^{-1}(x^{(i)} - \mu_0)\right) \\ + \sum_{i = 1}^{m}y^{(i)}\left(\log\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}-\frac{1}{2}(x^{(i)} - \mu_1)^T\Sigma^{-1}(x^{(i)} - \mu_1)\right) \\ = \sum_{i = 1}^{m}\log\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}} - \frac{1}{2}\sum_{i = 1}^{m}\left((x^{(i)} - \mu_1)^T\Sigma^{-1}(x^{(i)} - \mu_1)\right) \\ = \sum_{i = 1}^{m}\left(-\frac{n}{2}\log (2\pi) - \frac{1}{2}\log|\Sigma|\right) - \frac{1}{2}\sum_{i = 1}^{m}\left((x^{(i)} - \mu_1)^T\Sigma^{-1}(x^{(i)} - \mu_1)\right)$$

    在这个基础上，我们对上式求关于$\Sigma$的偏导数，进而有：

$$\frac{\partial l(\phi,\mu_0,\mu_1,\Sigma)}{\partial \mu_0} = \frac{1}{2}\sum_{i = 1}^{m}\left(\frac{1}{|\Sigma|}|\Sigma|\Sigma^{-1}\right) - \frac{1}{2}\sum_{i = 1}^{m}\left((x^{(i)} - \mu_1)^T(x^{(i)} - \mu_1)\Sigma^{-2}\right) \\ = 0$$
    上式在推导过程中用到了两个公式：
$$\frac{\partial |\Sigma|}{\partial \Sigma} = |\Sigma|\Sigma^{-1} \\ \frac{\partial \Sigma^{-1}}{\partial \Sigma} = \Sigma^{-2} \\ $$
    以下是一个二维高斯判别模型的示例，它们都的协方差矩阵都是$\Sigma$，但是它们的均值不等，分别是$\mu_0$和$\mu_1$，同样在图中的分界线表示$p(y = 1|x) = 0.5$。

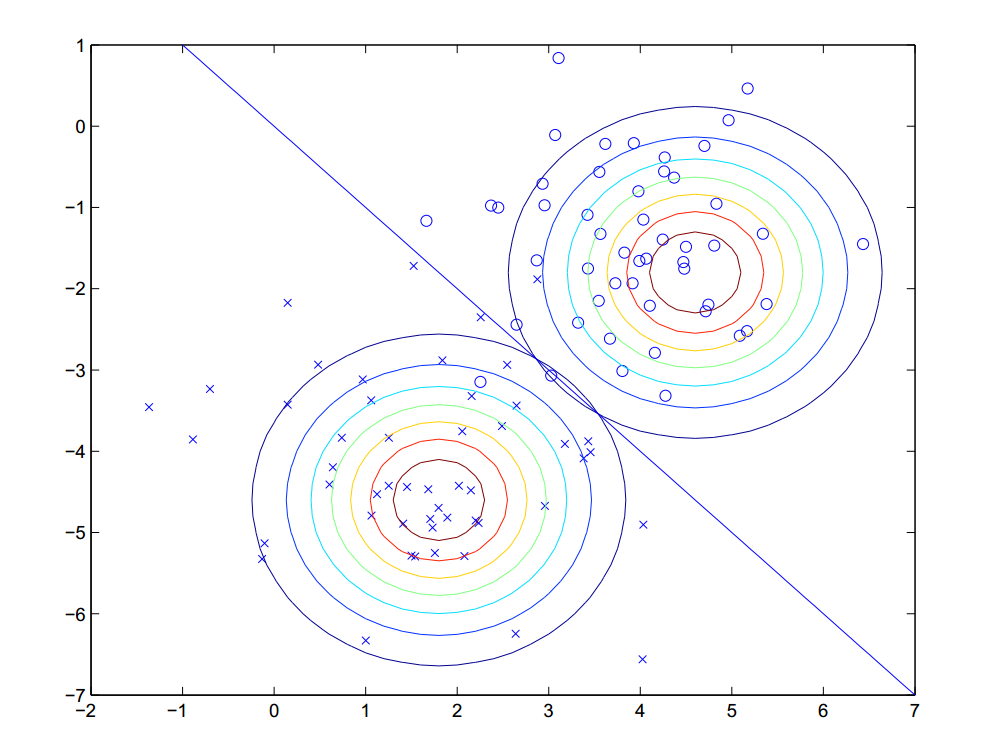
GDA模型与logistics模型的联系

       我们使用$p(y|x) = p(x|y)p(y)$进行拟合，对于$p(x|y)p(y)$我们可以进行归一化操作，可以得到：

$$p(y = 1|x) = \frac{p(x|y = 1)p(y = 1)}{p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)}$$
       实际上可以通过简单的转换转换成逻辑回归模型的形式：
$$p(y = 1|x;\phi,\mu_0,\mu_1,\Sigma) = \frac{1}{1 + e^{-\theta^Tx}}$$
       推导过程如下：
$$p(y = 1|x) = \frac{N(\mu_1,\Sigma)\phi}{N(\mu_1,\Sigma)\phi + N(\mu_0,\Sigma)(1 - \phi)} \\ = \frac{1}{1 + \frac{N(\mu_0,\Sigma)}{N(\mu_1,\Sigma)}\frac{1 - \phi}{\phi}}$$
     而对于$N(\mu_0,\Sigma)/N(\mu_1,\Sigma)$则有：
$$\frac{N(\mu_0,\Sigma)}{N(\mu_1,\Sigma)} = exp\left(x^{(i)} - \mu_0)^T\Sigma^{-1}(x^{(i)} - \mu_0) - (x^{(i)} - \mu_1)^T\Sigma^{-1}(x^{(i)} - \mu_1)\right) \\ = exp\left(2(\mu_1 - \mu_0)^T\Sigma^{-1}x + (\mu_0^T\Sigma\mu_0 - \mu_1^T\Sigma\mu_1)\right)$$
      那么，只需令：
$$2(\mu_1 - \mu_0)^T\Sigma^{-1} = (\theta_1, \theta_2,...,\theta_n) \\ \mu_0^T\Sigma\mu_0 - \mu_1^T\Sigma\mu_1 + \log \frac{1 - \phi}{\phi} = \theta_0$$
      其中$\theta$是关于$\phi,\mu_0,\mu_1,\Sigma$的函数。由此可见，逻辑回归模型比高斯判别分析模型更加普适，在建模上更加具有鲁棒性，而高斯判别模型则是逻辑回归模型的一种特殊形式。
       当数据服从高斯分布的时候，采用高斯判别分析模型效果会更好，这主要是由于使用了更多的信息进行建模，如果不服从高斯分布，往往逻辑回归构建的模型更加健壮一些。

补充

       从直观的讲，假设两个类的高斯分布协方差矩阵不同，一般都会更加合理（混合高斯模型），而且可以推导出上面简洁的结果。
       假定两个类具有不同的协方差矩阵，那么会有下面两点影响：

1. 当样本不充分是，使用不同的协方差矩阵会导致算法稳定性不够；过少的样本设置会协方差矩阵不可逆，从而使整个过程都无法进行。
2. 使用不同的协方差矩阵，最终分界线不会是线性的，同样也就无法推导出相应的逻辑回归形式了。

参考

机器学习实现与分析之五（高斯判别分析）
生成学习、高斯判别、朴素贝叶斯—斯坦福ML公开课笔记5
CS229机器学习笔记(四)-生成学习算法, 朴素贝叶斯, 多项式事件模型