朴素贝叶斯算法

机器学习 CS229

---

前言

       朴素贝叶斯是另一种生成学习算法，不过与高斯判别分析不同，朴素贝叶斯针对的则是特征向量$x$为离散值的情况。它比较典型的应用范围就是文本分类，以下也以文本分类为例对朴素贝叶斯进行简单的了解。

朴素贝叶斯分类器

       与其他分类算法相同，朴素贝叶斯算法也需要标注好的数据集，其中对于文本分类问题来说，一般采用向量空间模型（vector space model）来表示文本。下面是一个文本的表示示例：

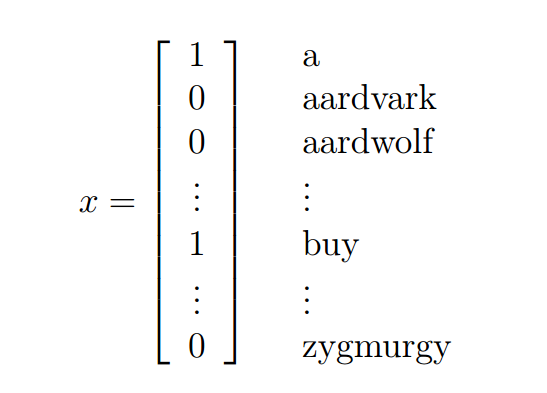
       如果我们的要对$p(x|y)$进行建模，其中$x \in \{0,1\}^n$，$n = 50000$，也就是意味着字典中有50000个单词，这样当我们直接对有$2^{50000}$种输出的多项分布$x$建模时，我们的参数向量就会达到$2^{50000} - 1$维（我认为这里指的应该就是参数向量$\theta$）（突然感觉好像离散值的分类算法用生成算法不是很赞啊 瞎猜的 待验证），客观的讲这是不现实的。而在朴素贝叶斯算法中，增加了一种理想化的假设，那就是特征向量$x$的所有维度都是不相关的，基于这种假设我们会有：

$$p(x_1,..,x_{50000}|y) = p(x_1|y)p(x_2|y,x_1)···p(x_{50000}|y,x_1,..,x_{49999}) \\ = \prod_{i = 1}^{m} p(x_i|y) \\ $$
       那么我们可以引入参数如下：
$$\phi_{j|y = 1} = p(x_i|y = 1) \\ \phi_{j|y = 0} = p(x_i|y = 0) \\ \phi_{y} = p(y)$$
       那么我们的联合似然函数为(其中$n$为字典大小)：
$$L(\phi_y,\phi_{i|y = 0},\phi_{i|y = 1}) = \prod_{i = 1}^{m}p(x^{(i)},y^{(i)}) \\ = \prod_{i = 1}^{m}\left(\prod_{j = 1}^{n}p(x_j^{(i)}|y^{(i)})\right)p(y^{(i)})$$
       其中：
$$p(y^{(i)}) = \phi_y^{y^{(i)}}(1 - \phi_y)^{1 - y^{(i)}} \\ p(x^{(i)}|y^{(i)}) = \prod_{j = 1}^np(x_j^{(i)}|y^{(i)}) \\ p(x_j^{(i)}|y^{(i)})=\left(\phi_{j|y=0}^{1\{x_j^{(i)}=1\}}(1-\phi_{j|y=0})^{1-1\{x_j^{(i)}=1\}}\right)^{1\{y^{(i)}=0\}} \cdot\left(\phi_{j|y=1}^{1\{x_j^{(i)}=1\}}(1-\phi_{j|y=1})^{1-1\{x_j^{(i)}=1\}}\right)^{1\{y^{(i)}=1\}}$$
       那么带入公式我们可以有：

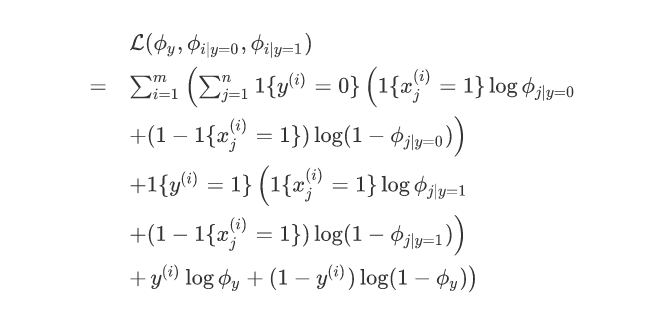
       接下来我们分别对他们求偏导数：



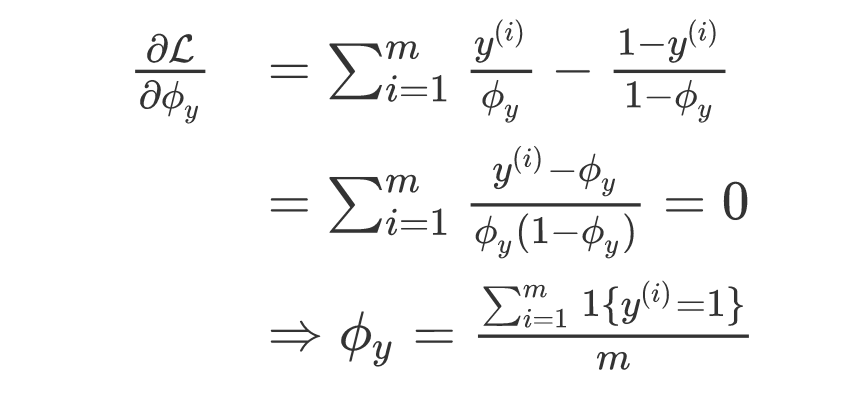
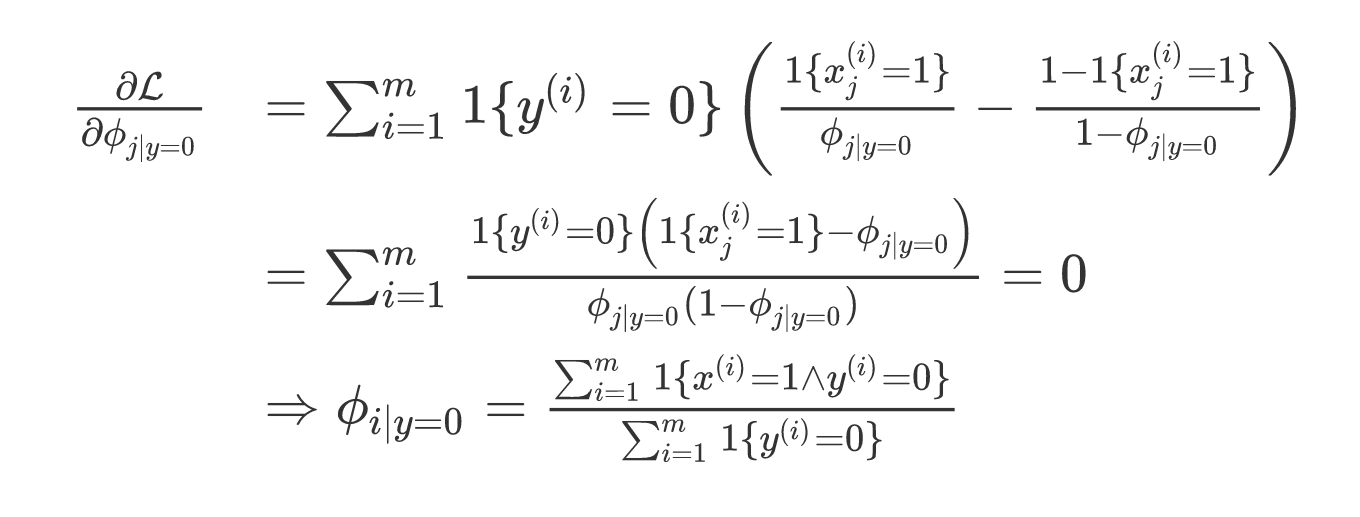
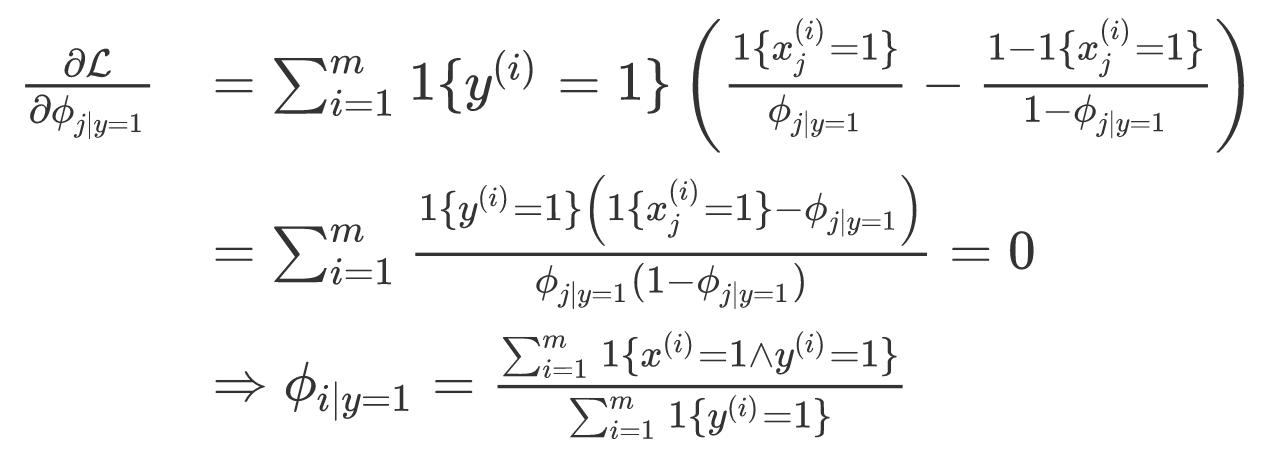
       对于新样本我们可以通过公式很容易的得到计算结果：

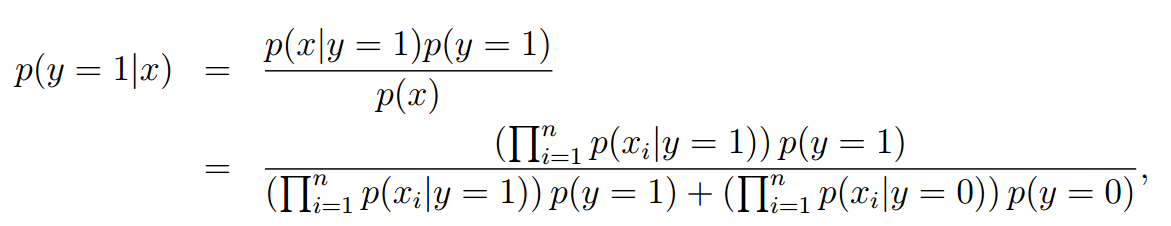
       但是由于概率的取值范围为$[0,1]$，多个概率相乘的结果可能会非常小，以至于产生下溢出，所以我们可以取对数进行等价处理。

拉普拉斯平滑

       拉普拉斯平滑，主要是用于解决零概率的问题，又被成为+1平滑。
       给定$m$个训练样本$\{z^{(1)},...,z^{(m)}\}$，那么根据最大似然估计求出的参数$\phi_i=\left(\sum_{i=1}^m1\{z^{(i)}=j\}+1\right)/(m+k)$。如果特征$z^{(i)} = j$在训练集上，那么$\phi_j = 0$，仅仅由于在训练集上未出现就就将概率设置为0在统计学上是十分不合理的。为了避免这种情况，我们引入了拉普拉斯平滑，通过分子分母在原来的统计基础上增加一个常数，来达到平滑的目的。

$$\begin{equation*} \phi_y=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}+1}{m+2} \end{equation*}$$
$$\begin{equation*} \phi_{i|y=1}=\frac{\sum_{i=1}^m1\{x^{(i)}=1\land y^{(i)}=0\}+1}{\sum_{i=1}^m1\{y^{(i)}=0\}+2} \end{equation*}$$
$$\begin{equation*} \phi_{i|y=0}=\frac{\sum_{i=1}^m1\{x^{(i)}=1\land y^{(i)}=0\}+1}{\sum_{i=1}^m1\{y^{(i)}=0\}+2} \end{equation*}$$

多项分布型朴素贝叶斯

       现在对当前的内容进行适当地扩展，我们不在认为$x_i \in \{0,1\}$，而是$x_i \in \{1,2,...,n\}$，相对于之前我们的参数公式来说，$p(y^{(i)})$和$p(x^{(i)}|y^{(i)})$，与之前是完全相同的，而$p(x_j^{(i)}|y^{(i)})$则发生了较大的变化：

$$p(x_j^{(i)}|y^{(i)}) =\left(\prod_{k=1}^{n}\phi_{k|y^{(i)}=0}^{1\{x_j^{(i)}=k\}}\right)^{1\{y^{(i)}=0\}}\left(\prod_{k=1}^{n}\phi_{k|y^{(i)}=1}^{1\{x_j^{(i)}=k\}}\right)^{1\{y^{(i)}=1\}}$$
       那么，似然函数的形式如下：
$$L(\phi_y,\phi_{k|y=0},\phi_{k|y=1}) =\prod_{i=1}^mp(x^{(i)},y^{(i)})\\ =\prod_{i=1}^m\left(\prod_{j=1}^{n}p(x_j^{(i)}|y^{(i)};\phi_{k|y=0},\phi_{k|y=1})\right)p(y^{(i)};\phi_y)$$
       考虑到存在约束条件$\sum_{i=1}^{n}\phi_{k|y=0}=1$和$\sum_{i=1}^{n}\phi_{k|y=1}=1$，我们在似然函数的对数形式中引入拉格朗日乘子，得到如下函数：
$$l(\phi_y,\phi_{k|y=1},\phi_{k|y=1})\\ =\sum_{i=1}^m\left(\sum_{j=1}^{n}\log p(x^{(i)}_j|y^{(i)})+\log p(y^{(i)})\right)\\ +\lambda_1\left(\sum_{k=1}^{n}\phi_{k|y=0}-1\right)+\lambda_2\left(\sum_{k=1}^{n}\phi_{k|y=1}-1\right)\\ =\sum_{i=1}^m\left[\sum_{j=1}^{n}\left(1\{y^{(i)}=0\}\sum_{k=1}^{n}1\{x_j^{(i)}=k\}\log\phi_{k|y=0}\\ +1\{y^{(i)}=1\}\sum_{k=1}^{n}1\{x_j^{(i)}=k\}\log\phi_{k|y=1}\right)\\ +y^{(i)}\log\phi_y+\left(1-y^{(i)}\right)\log\left(1-\phi_y\right)\right]\\ +\lambda_1\left(\sum_{k=1}^{n}\phi_{k|y=0}-1\right)+\lambda_2\left(\sum_{k=1}^{n}\phi_{k|y=1}-1\right)$$
       接下来采用最大似然估计的方式，对各个参数求偏导：
$$\frac{\partial l}{\partial\phi_y}=\sum_{i=1}^m\frac{y^{(i)}}{\phi_y}-\frac{1-y^{(i)}}{1-\phi_y}\\ =\sum_{i=1}^m\frac{y^{(i)}-\phi_y}{\phi_y(1-\phi_y)}\\ \Rightarrow\phi_y=\frac{\sum_{i=1}^my^{(i)}}{m}=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}}{m}$$
$$\frac{\partial l}{\partial\phi_{k|y=0}} =\sum_{i=1}^m\sum_{j=1}^{n}\frac{1\{x_j^{(i)}=k\land y^{(i)}=0\}}{\phi_{k|y=0}}+\lambda_1=0\\ \Rightarrow\phi_{k|y=0}=-\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k\land y^{(i)}=0\}}{\lambda_1}$$
$$\frac{\partial l}{\partial\phi_{k|y=1}} =\sum_{i=1}^m\sum_{j=1}^{n}\frac{1\{x_j^{(i)}=k\land y^{(i)}=1\}}{\phi_{k|y=1}}+\lambda_2=0\\ \Rightarrow\phi_{k|y=1}=-\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k\land y^{(i)}=1\}}{\lambda_2}$$
       又因为$\sum_{k=1}^n\phi_{k|y=0}=1$和$\sum_{k=1}^{n}\phi_{k|y=1}=1$，结合上式我们可以得到：
$$\lambda_1=-\sum_{i=1}^m\sum_{j=1}^{n}\sum_{k=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=0\}=-\sum_{i=1}^m1\{y^{(i)}=0\}n$$
$$\lambda_2=-\sum_{i=1}^m\sum_{j=1}^{n}\sum_{k=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=1\}=-\sum_{i=1}^m1\{y^{(i)}=1\}n$$
       接下来我们将$\lambda_1$和$\lambda_2$带入，则有：
$$\phi_{k|y=0}=\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=0\}}{\sum_{i=1}^m1\{y^{(i)}=0\}n}$$
$$\phi_{k|y=1}=\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=1\}}{\sum_{i=1}^m1\{y^{(i)}=1\}n}$$
       观察求出来的参数，我们对其进行拉普拉斯平滑：
$$\phi_y=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}+1}{m+2}$$
$$\phi_{k|y=0}=\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=0\} + 1}{\sum_{i=1}^m1\{y^{(i)}=0\}n + n}$$
$$\phi_{k|y=1}=\frac{\sum_{i=1}^m\sum_{j=1}^{n}1\{x_j^{(i)}=k \land y^{(i)}=1\} + 1}{\sum_{i=1}^m1\{y^{(i)}=1\}n + n}$$
       那么最终导出的分类准则如下：
$$\hat{y}=\underset{y\in\{0,1\}}{\arg\max}\;p(y|x)=\underset{y\in\{0,1\}}{\arg\max}\left(\log p(y)+\sum_{j=1}^{n_i}\log p(x_j|y)\right)$$

朴素贝叶斯与连续型数据

       对于前面说的两种朴素贝叶斯分类器都只适用于离散型随机变量，如果遇到连续型的数据该如何处理呢？对于这种问题可以采用两种常用的方法：概率分布估计和离散化。

概率分布估计

       对于连续型数据，我们通常假设该数据在每类样本中都各自服从高斯分布$\mathcal{N}(\mu_0,\sigma_0^2)$和$\mathcal{N}(\mu_1,\sigma_1^2)$（做出其他分布假设也是可以的，但是一般都采用高斯分布模型）。由于在朴素贝叶斯中假设样本每一个属性都是条件独立的，那么每一个属性都可以有不同的概率分布，如下图所示：

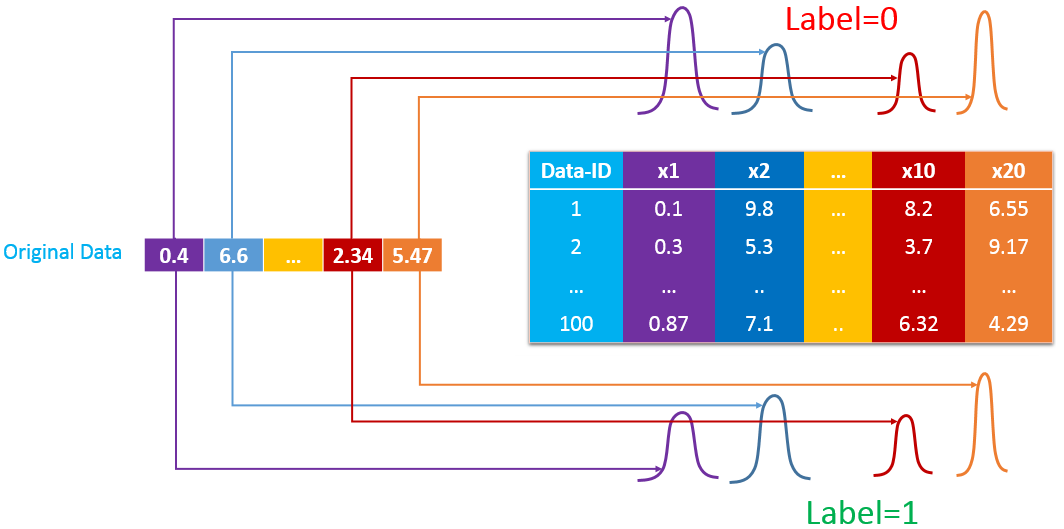
       此时我们的模型参数包括一个伯努利分布的参数$\phi_y = p(y = 1)$和$4n$个高斯分布的模型参数$\mu_{j|y = 0}$、$\sigma_{j|y=0}$、$\mu_{j|y=1}$和$\sigma_{j|y=1}$。模型中的概率关系如下：

$$p(y)=\phi_y^{y}(1-\phi_y)^{1-y}$$
$$p(x|y)=\prod_{i=1}^np(x_i|y)$$
$$p(x_i|y)=\left(\frac{1}{\sqrt{2\pi\sigma_0^2}}\exp\left(-\frac{(x_i-\mu_0)^2}{2\sigma_0^2}\right)\right)^{1\{y=0\}}\left(\frac{1}{\sqrt{2\pi\sigma_1^2}}\exp\left(-\frac{(x_i-\mu_1)^2}{2\sigma_1^2}\right)\right)^{1\{y=1\}}$$
       还是假设我们有$m$个训练样本，那么我们会有如下的似然函数：
$$L(\phi_y,\mu_{k|y=0},\sigma_{k|y=0}^2,\mu_{k|y=1},\sigma_{k|y=1}^2)\\ =\prod_{i=1}^mp\left(x^{(i)},y^{(i)}\right)\\ =\prod_{i=1}^m\left(\prod_{j=1}^np\left(x_j^{(i)}|y^{(i)}\right)\right)p(y^{(i)})$$
       将上述函数转换成对数形式：
$$l(\phi_y,\mu_{k|y=0},\sigma_{k|y=0}^2,\mu_{k|y=1},\sigma_{k|y=1}^2)\\ =\sum_{i=1}^m\left(\sum_{j=1}^n\log p\left(x_j^{(i)}|y^{(i)}\right)+\log p\left(y^{(i)}\right)\right)\\ =-\frac{1}{2}\sum_{i=1}^m\left[\sum_{j=1}^n1\{y^{(i)}=0\}\left(\frac{\left(x_j^{(i)}-\mu_{j|y=0}\right)^2}{\sigma_{j|y=0}^2}+\log\sigma_{j|y=0}^2\right)\right.\\ \left.+1\{y^{(i)}=1\}\left(\frac{\left(x_j^{(i)}-\mu_{j|y=1}\right)^2}{\sigma_{j|y=1}^2}+\log\sigma_{j|y=1}^2\right)\right]\\ \quad+y^{(i)}\log\phi_y+\left(1-y^{(i)}\right)\log(1-\phi_y)+const$$
       对各个参数求偏导数：
$$\frac{\partial l}{\partial\phi_y} =-\frac{1}{2}\sum_{i=1}^m\frac{y^{(i)}}{\phi_y}-\frac{1-y^{(i)}}{1-\phi_y}\\ =\frac{1}{2}\sum_{i=1}^m\frac{\phi_y-y^{(i)}}{\phi_y(1-\phi_y)}=0\\ \Rightarrow\phi_y=\frac{\sum_{i=1}^my^{(i)}}{m}$$
$$\frac{\partial l}{\partial\mu_{j|y=0}}=-\sum_{i=1}^m1\{y^{(i)}=0\}\frac{\left(x_j^{(i)}-\mu_{j|y=0}\right)}{\sigma_{j|y=0}^2}=0\\ \Rightarrow \mu_{j|y=0}=\frac{\sum_{i=1}^m1\{y^{(i)}=0\}x_j^{(i)}}{\sum_{i=1}^m1\{y^{(i)}=0\}}$$
       同理可得：
$$\mu_{j|y=1}=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}x_j^{(i)}}{\sum_{i=1}^m1\{y^{(i)}=1\}}$$
       我们继续求方差的偏导数：
$$\frac{\partial\mathcal{L}}{\partial\sigma_{j|y=0}} =\sum_{i=1}^m1\{y^{(i)}=0\}\left(\frac{\left(x_j^{(i)}-\mu_{j|y=0}\right)^2}{\sigma_{j|y=0}^3}-\frac{1}{\sigma_{j|y=0}}\right)=0\\ \Rightarrow\sigma_{j|y=0}^2=\frac{\sum_{i=1}^m1\{y^{(i)}=0\}\left(x_j^{(i)}-\mu_{j|y=0}\right)^2}{\sum_{i=1}^m1\{y^{(i)}=0\}}$$
       同理可得：
$$\sigma_{j|y=1}^2=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}\left(x_j^{(i)}-\mu_{j|y=1}\right)^2}{\sum_{i=1}^m1\{y^{(i)}=1\}}$$
       实际上，$\phi_y$就是训练集中正样本出现的频率，$\mu_{j|y = 0}$和$\mu_{j|y = 1}$则分别表示正样本和负样本的第$j$维均值，$\sigma_{j|y=0}^2$和$\sigma_{j|y=1}^2$分别表示正样本和负样本特征第$j$维的方差。

离散化

       对于连续值的问题也可以将其离散化为$k$个有限的离散值(一般$k = 10$)，这样就转化成多项分布的朴素贝叶斯算法了。假设我们有很多维联系的特征需要离散化处理，如下图所示，第一维数据被划分为两个区间，第二维数据被划分为四个区间，如果原始数据第一维和第二维分别落入第二个和第三个，那么离散化后的数值分别为2和3。

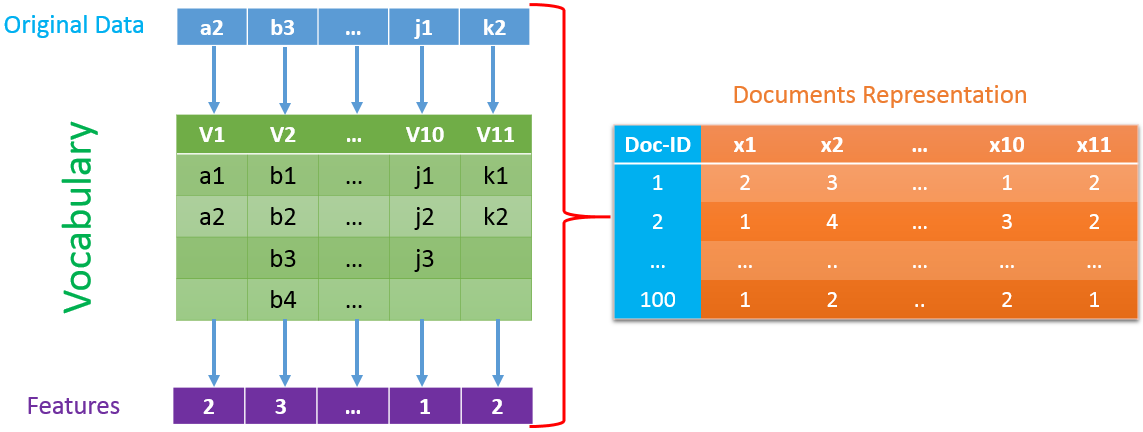
       在这里我们假设每一维的数据都是连续值，原始特征的第$j$维连续数据经离散化后变成了$k_j$个离散数据，每个样本对应的标签信息$y \in \{0,1\}$。所以模型之中存在的参数以及概率关系与多项分布的朴素贝叶斯模型是相同的，所以就不再继续推导一遍了（这种方法在Ng的讲义中也提及到了）。

概率分布与离散化的选择

       上面两种方案在使用过程中该如何选择呢？一般来说，如果训练数据较少或者我们大致知道数据的概率分布，那么选择概率分布模型效果会比较好；当有大量训练数据时，往往离散化的方法也会有不错的表现，这是由于其模型相对更加复杂（？？？），整个学习过程实际上是在不断拟合数据的实际概率分布，而概率分布模型则是假设数据满足了某种概率分布进行学习过程的，就如同在之前的文章中提到了的。
       一般来说，朴素贝叶斯模型更多的被用于有大量训练数据的应用场景，所以离散化的技术手段使用的也更加广泛些。根据我们的经验，简单的模型容易产生欠拟合的现象，而复杂的模型容易产生过拟合的情况。在训练数据比较小的时候，由于复杂模型比较容易出现过拟合的问题，所以简单模型的泛化能力要比复杂模型好一些，但这时两者都只能学习到数据中的极少数特点；当数据很充足时，简单模型则会出现欠拟合的问题，其泛化能力并不会因训练集的增大而增强，这时就是复杂模型更加适用的情况了。

结语

       本篇文章大量借鉴了参考一中的内容，在看到这篇文章之后，我几乎把整篇文章重写了一遍，从某些程度而言，我就是将那篇文章中前后不一致的地方一致化，同时去掉一些我认为不需要的地方，需要注意的是之前我一直以为$1\{y^{(i)}=1\}$其中的$1$是$I$，所以在我的博客中会出现不一致的现象，对于之前的我就不再进行改动了，但是之后的文章则会对这一部分进行修改。

参考

Naive Bayes Algorithm（写的非常好）
生成学习、高斯判别、朴素贝叶斯—斯坦福ML公开课笔记5