马氏距离

机器学习 统计学

---

前言

       马氏距离是一种表示数据的协方差距离的方式，它是一种有效的计算两个位置样本及的相似度的方法。与欧氏距离不同的是它考虑到了各种特性之间的联系并且是尺度无关的，即独立于测量尺度。

马氏距离

       对于一个均值为$\mu =(\mu _{1},\mu _{2},\mu _{3},\dots ,\mu _{p})^{T}$，协方差为$\Sigma$的多变量向量$x=(x_{1},x_{2},x_{3},\dots ,x_{p})^{T}$，其马氏距离为：

$$D_{M}(x)={\sqrt {(x-\mu )^{T}\Sigma ^{{-1}}(x-\mu )}}$$
       马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为$\Sigma$的随机变量$\vec x$与$\vec y$的差议程度：
$$d({\vec {x}},{\vec {y}})={\sqrt {({\vec {x}}-{\vec {y}})^{T}\Sigma ^{{-1}}({\vec {x}}-{\vec {y}})}}$$
       如果协方差矩阵为单位矩阵，那么马氏距离就简化为欧氏距离；如果协方差矩阵为对角矩阵，其也可称为正规化的欧式距离：
$$d({\vec {x}},{\vec {y}})={\sqrt {\sum _{{i=1}}^{p}{(x_{i}-y_{i})^{2} \over \sigma _{i}^{2}}}}$$
其中$\sigma_i$是$x_{i}$的标准差。

几何解释

       上面的公式之类的还是比较容易理解的，但是这其中的原理到底是什么？首先，我们先对协方差矩阵进行奇异值分解：

$$\Sigma = U\Lambda U^T$$
       那么，我们有：
$$\Sigma^{-1} = (U^T)^{-1}\Lambda^{-1} U^{-1} \\ = U\Lambda^{-1} U^T = \sum_{i = 1}^{D}\frac{1}{\lambda_i}u_iu_i^T$$
       根据马氏距离的定义有：
$${(x-\mu )^{T}\Sigma ^{{-1}}(x-\mu )} = {(x-\mu )^{T}\left(\sum_{i = 1}^{D}\frac{1}{\lambda_i}u_iu_i^T\right)(x-\mu )} \\ = \sum_{i = 1}^{D}\frac{1}{\lambda_i}(x-\mu )^{T}u_iu_i^T(x-\mu )$$
       在这里我们定义一个矩阵$F$，其中$F^T = UX^T$，由于之前的定义我们可以知道$U$是一个旋转矩阵，所以上述过程只改变了向量的方向并未对大小产生影响。
       我们将新矩阵的记为$\mu_F$，那么很显然我们会有：
$$(F - \mu_F)^T = U(X - \mu_X)^T \\ F - \mu_F = (X - \mu_X)U^T$$
所以，我们可以求出矩阵$F$的协方差矩阵：
$$\Sigma_F = E((F - \mu_F)^T(F - \mu_F)) \\ = E(U(X - \mu_X)^T(X - \mu_X)U^T) \\ = E(U\Sigma U^T) \\ = {\begin{bmatrix}\lambda_{1}&&\\&\ddots &\\&&\lambda_{k}\end{bmatrix}}$$
       对于我们在之前推导的式子有：
$${(x-\mu )^{T}\Sigma ^{{-1}}(x-\mu )} = = \sum_{i = 1}^{D}\frac{f_i^Tf_i}{\lambda_i}$$
       我们再来简述一下上述的过程，在马氏距离的计算过程中，首先通过旋转矩阵$U$对$X$进行了旋转，再根据方差$\lambda$进行放缩，最后就是简单的欧式距离的计算就可以得到我们需要的马氏距离了，基本的过程如下图所示，不过需要注意的是除下图一外其他的图片都已经发生了坐标的变换。

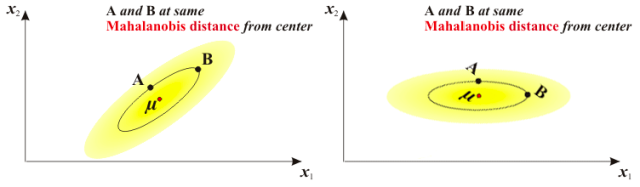
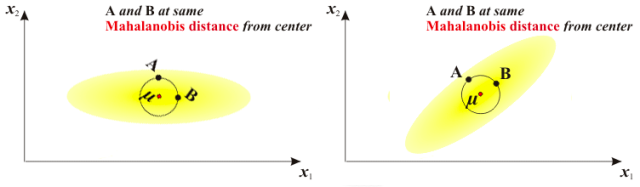
结语

       本篇文章基本上就先聊到这里，关于协方差矩阵是奇异矩阵事情还没有遇到过，等遇到了可能会在本篇文章补充一下相关内容，基本就是这样子。

参考

马氏距离
旋转矩阵
马氏距离及其几何解释
马氏距离+协方差公式+无偏估计